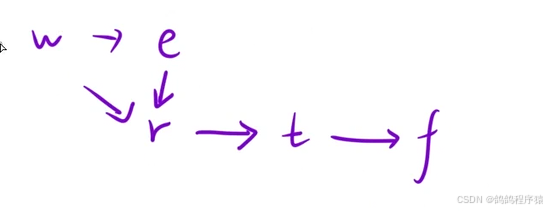【算法】【优选算法】BFS 解决拓扑排序

一、拓扑排序

1.1 有向无环图（DAG图）

有向无环图：有向无环图：一个无回路的有向图，如果一个有向图无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG图）。

1.2 AOV 网：顶点活动图

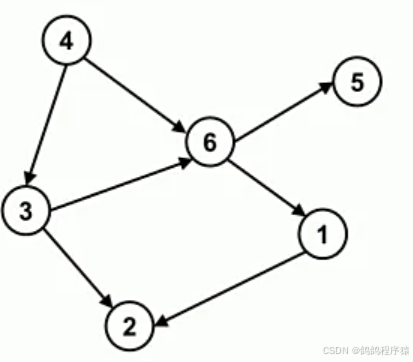
在有向无环图的基础上，用顶点来表示一个活动，用边来表示活动执行的先后顺序。

1.3 拓扑排序

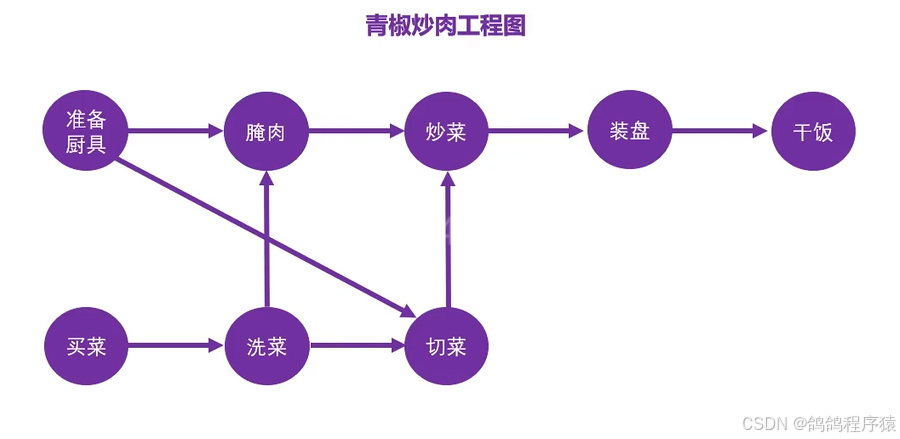
拓扑排序： 拓扑排序，找到做事的先后顺序。每次出入度为0的点，并且删除该点相连的边，排序进行。

1.4 实现拓扑排序

1. 找出图中入度为0的点
2. 删除与该点连接的变
3. 重复1 2 直到没有点 或者 没有入度为0 的点。

借助队列，来一次BFS

1. 初始化：把所有入度为0的点加入到队列
2. 当队列不为空：
3. 1. 拿出队头元素，加入到最终结果
4. 2. 删除与元素相连的边
5. 3. 判断：与删除的边相连的点，入度是否变为0

二、207. 课程表

题目链接：207. 课程表

题目描述：

• 

题目解析：

• 给我们一个int数，代表id为 0 到 numCourses 的课程，
• 给我们一个 prerequisites 数组，其中从后往前代表学习顺序
• 让我们看能否排课，将课程学完，必须保证学习顺序

解题思路：

• 我们使用二维数组List<List>，来表示图，每一个下标对应的一维数组，表示该点指向的点；
• 我们遍历一次prerequisites数组，将最后的n-1列的值当成点，其余入该点对应的一维数组。除了n-1列，其余对应的入度数组对应下标值加一。
• 在进行一次BFS即可
• 注意事项：每个点只能入一次队，prerequisites可以是 [ ] 数组，在前面要排除。
  解题代码：

//O(M*N)
//O(M*N)
class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {int m = prerequisites.length;if(m == 0) return true;int n = prerequisites[0].length;//建图List<List<Integer>> edges = new ArrayList<>();for(int i = 0; i < numCourses; i++) {edges.add( new ArrayList<>() );}Queue<Integer> queue = new LinkedList<>();//记录下标对应每个点的入度int[] in = new int[numCourses];//标记入过队的元素boolean[] flag = new boolean[numCourses];//记录入度for(int i = 0; i < m; i++) {for(int j = 0; j < n-1; j++) {//建图edges.get(prerequisites[i][n-1]).add(prerequisites[i][j]);//统计入度in[prerequisites[i][j]]++;}}//入度为0的点入队for(int i = 0; i < numCourses; i++) {if(in[i] == 0) {queue.add(i);flag[i] = true;}}if(queue.isEmpty()) return false;//BFSwhile(!queue.isEmpty()) {int tmp = queue.poll();//销毁边for(int i = 0; i < edges.get(tmp).size(); i++) {in[edges.get(tmp).get(i)]--;}//入度为0的点入队for(int i = 0; i < numCourses; i++) {if(in[i] == 0 && !flag[i]){queue.add(i);flag[i] = true;} }}//还有入度不为0的点for(int i = 0; i < numCourses; i++) {if(in[i] != 0){return false;} }return true;}
}

三、210. 课程表 II

题目链接：210. 课程表 II

题目描述：

• 

题目解析：

• 给我们一个int数，代表id为 0 到 numCourses 的课程，
• 给我们一个 prerequisites 数组，其中从后往前代表学习顺序
• 让我们看能否排课，将课程学完，必须保证学习顺序，返回学习的顺序，不行就返回空数组。
  解题思路：
• 我们使用二维数组List<List>，来表示图，每一个下标对应的一维数组，表示该点指向的点；
• 我们遍历一次prerequisites数组，将最后的n-1列的值当成点，其余入该点对应的一维数组。除了n-1列，其余对应的入度数组对应下标值加一。
• 在进行一次BFS即可，每次出的点都进入结果数组
• 注意事项：
• • 我们先将结果数组初始化为 0 到 numCourses-1 ，，prerequisites可以是 [ ] 数组时直接就返回
• • 当最后执行完，我们使用一个计数器lep来标记进入结果数组的元素，最后只需要比较lep与numCourses是否一样，一样返回结果数组，不一样返回空数组。
    解题代码：

//O(M*N)
//O(M*N)
class Solution {public int[] findOrder(int numCourses, int[][] prerequisites) {//结果数组int[] ret = new int[numCourses];for(int i = 0; i < numCourses;i++) ret[i] = i;int m = prerequisites.length;if(m == 0) return ret;int n = prerequisites[0].length;Queue<Integer> queue = new LinkedList<>();//标记数组boolean[] flag = new boolean[numCourses];//入度数组int[] in = new int[numCourses];//建图List<List<Integer>> edges = new ArrayList<>();for(int i = 0; i < numCourses; i++) {edges.add(new ArrayList<>());}//记录入度，初始图for(int i = 0; i < m; i++) {for(int j = 0; j < n-1; j++) {edges.get(prerequisites[i][n-1]).add(prerequisites[i][j]);in[prerequisites[i][j]]++;}}//入度为0的点入队for(int i = 0; i < numCourses; i++) {if(in[i] == 0) {flag[i] = true;queue.add(i);}}//BFSint lep = 0;while(!queue.isEmpty()) {int tmp = queue.poll();ret[lep++] = tmp;//删去该点出的边for(int i = 0; i < edges.get(tmp).size(); i++) {in[edges.get(tmp).get(i)]--;}//入队for(int i = 0; i < numCourses; i++) {if(in[i] == 0 && !flag[i]) {queue.add(i);flag[i] = true;}}}if(lep != numCourses) return new int[]{};return ret;}
}

四、LCR 114. ⽕星词典

题目链接：LCR 114. ⽕星词典

题目描述：

• 

题目解析：

• 给我们一个字符串数组words，
• 两个字符串对比来得出字母顺序，两个字符串第一个不相同的字母的顺序 等于 两个字符串在数组中的顺序，如示例一第一个字符串“wrt” 和 第二个字符串“wrf” 得出的字母顺序就是 t->f
• 将所有的字符两两对比，得出字母顺序，不能得出线性顺序就返回空字符串“”

解题思路：

• 两层for循环，先搜索两个规则导致的排序结果建立图，例如示例一就建立这个图
• • 
• 根据图拓扑排序 ，得出结论
• 细节问题： abc 和 ab，并且abc在数组中位于ab前面，这种是不合法的
  解题代码：

//O(M*N)
//O(M*N)
class Solution {//图Map<Character, Set<Character>> edges = new HashMap<>();//入度Map<Character, Integer> in = new HashMap<>();//标记有没有abc ab这种不合法boolean flag;public String alienOrder(String[] words) {//初始化入度for(String s : words) {for(int i = 0; i < s.length(); i++) {char ch = s.charAt(i);in.put(ch,0);}}//建图for(int i = 0; i < words.length; i++) {for(int j =  i + 1; j <words.length; j++) {//统计两个字符串的字母顺序add(words[i], words[j]);if(flag == true) return "";}}//拓扑排序初始化Queue<Character> queue = new LinkedList<>();for(char ch : in.keySet()) {if(in.get(ch) == 0) queue.add(ch);}//BFSStringBuffer ret = new StringBuffer();while(!queue.isEmpty()) {char tmp = queue.poll();ret.append(tmp);if(!edges.containsKey(tmp)) continue;for(char ch : edges.get(tmp)) {in.put(ch, in.get(ch)-1);if(in.get(ch) == 0) {queue.add(ch);}}}for(char ch : in.keySet()) {if(in.get(ch) != 0) return "";}return ret.toString();}public void add(String a, String b) {int i = 0;int n = Math.min(a.length(), b.length());for( ; i < n; i++) {char ch1 = a.charAt(i);char ch2 = b.charAt(i);if(ch1 != ch2) {//ch1 -> ch2if(!edges.containsKey(ch1)) {edges.put(ch1, new HashSet<>());}if(!edges.get(ch1).contains(ch2)) {edges.get(ch1).add(ch2);in.put(ch2,in.get(ch2) + 1);}break;}}if(i == b.length() && a.length() > i) flag = true;}
}