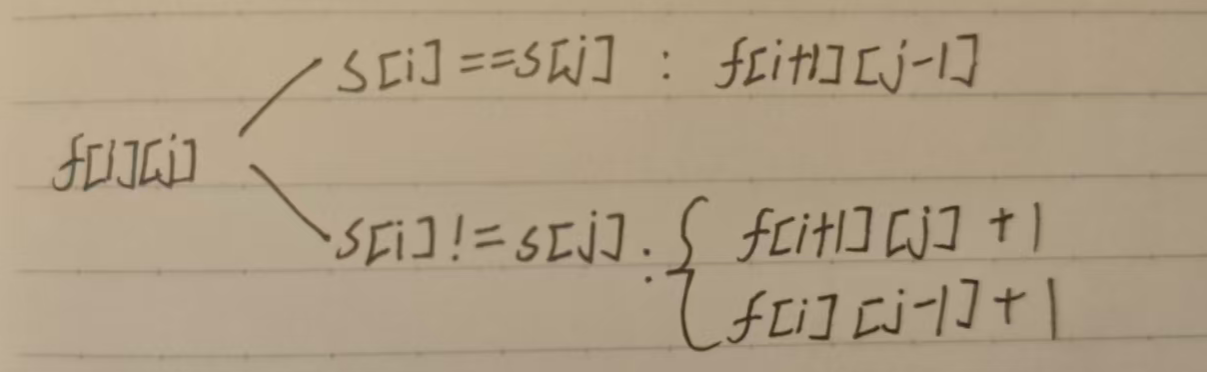算法题（227）：回文字符串

审题：

本题需要我们找出将给定字符串变为回文字符串的最少插入字符数

思路：
方法一：动态规划

我们可以先分析某个子区间的最少插入字符数，然后递推到最终整个字符串的最少插入字符数

（1）状态表示：

f[i][j]表示在左端点为第i个字符，右端点为第j个字符的区间内，将该区间字符串变为回文串的最少插入字符数

（2）状态转移方程：
可以分为两种情况

一种是当前左右端点已经相等，只需要找到将左右端点内的区间变为回文串的最少插入个数另一种是当前左右端点不相等，需要分为左端点前加字符和右端点后加字符两种情况

（3）填表顺序：

区间dp的遍历方式和其他的dp问题有不同，他有自己独特的遍历方式

第一层for循环：让区间长度len从1~n遍历

第二层for循环：左端点从2~(i+len-1)遍历

第一层for循环解释：

可以保证f[i][j]更新所需的节点已经被更新完，比如求len=5的f[i][j]，此时len=4/3/2/1的所有情况都已经被求出来了，而len=5所依赖的节点一定是len<5的，所以一定可以求出结果

第二层for循环解释：
正常来说左端点可以从1~n遍历，但是由于左端点（i）<=右端点（j），所以为了防止j越界，我们要让j（i+len-1）小于等于n，且由于1所依赖的节点是非法节点，可能会出现问题，所以我们从2开始遍历最好（不过本题中非法位置都为0，不影响结果）

（4）初始化：
我们只要初始化len=1的情况就行，而len=1的情况说明只有一个字符，一定是回文串，初始化为0即可

（5）答案输出：
直接输出f[1][n]即可

解题：
 

#include<iostream>
using namespace std;
const int N = 1010;
string s;
int f[N][N];
int main()
{cin >> s;int n = s.size();//填表for (int len = 1; len <= n; len++){for (int i = 2; i + len - 1 <= n; i++){int j = i + len - 1;if (s[i-1] == s[j-1]){f[i][j] = f[i + 1][j - 1];}else{f[i][j] = min(f[i + 1][j], f[i][j - 1]) + 1;}}}//答案输出cout << f[1][n] << endl;return 0;
}

注意：由于我们的状态表示中的i表示第i个字符，而字符串的第i个字符索引是i-1，所以我们需要在判断的时候特殊处理一下

P1435 [IOI 2000] 回文字串 - 洛谷