磁共振成像原理（理论）19：基本成像原理 (Basic Imaging Methods) - 三维成像

之前的内容介绍到：在没有梯度磁场的情况下，射频脉冲激励后产生的信号（FID信号和Echo信号）将来自整个三维成像物体（该成像物体一般就是三维的）。

换句话说，从整个物体产生信号比从有限区域产生信号更容易。三维成像的挑战在于区分来自不同空间位置的所有信号分量。实现这一目标的方法有很多，最简单的大概是多切片成像方法，该方法：

• 首先基于选层梯度+射频脉冲进行选择性激发，把三维问题降低到二维；
• 然后通过二维编码，即相位编码和频率编码完成K空间覆盖。

在施加射频脉冲时同时施加选层梯度，可将上述三维成像转化为多个切片成像，而每一个切片成像都是二维成像。因此，该方法通常会产生多个二维图像。

对于真正的三维成像，使用非选择性脉冲进行信号生成，所有三维信息必须编码到激活信号中。由于磁共振信号的性质，沿一维的信息自然进行频率编码，而沿其他二维的信息可以进行相位或频率编码。无论采用何种编码方案，通用成像方程均为三维傅里叶变换形式：

$$S(k_x,k_y,k_z)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }I(x,y,z)e^{-i2\pi (k_{x}x+k_{y}y+k_{z}z)}dxdydz\text{\hspace{1em}(5.110)}$$

其中 $S(k_x,k_y,k_z)$ 表示$k$空间信号，$I(x,y,z)$ 表示三维物体分布函数。该方程建立了图像空间与$k$空间之间的傅里叶变换关系，是三维磁共振成像的数学基础。

不同编码方案仅导致三维$k$空间的不同采样模式。为证明此点，考虑下图所示的三维相位编码成像序列.

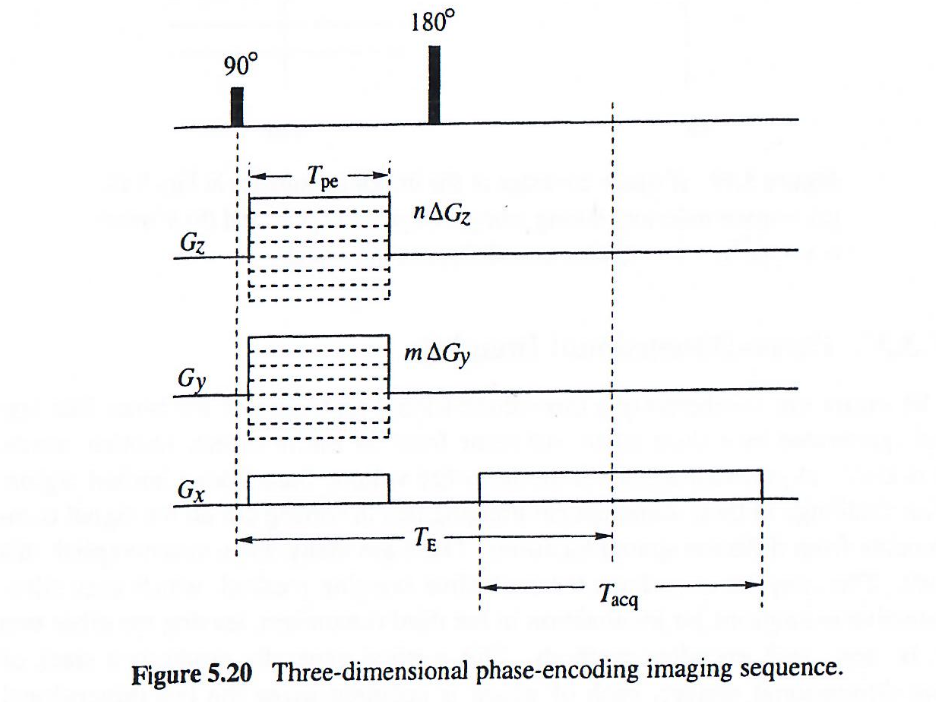
其中$x$方向进行频率编码，而$y$和$z$方向进行相位编码。在这种情况下，$k$空间由平行于 $k_x$ 轴的直线填充，其数学描述为：
$$\{\begin{array}{l}{k}_x=\bar{\gamma }{G}_x(t-T_E)\\ k_y=\bar{\gamma }{G}_y{T}_{pe}\\ k_z=\bar{\gamma }{G}_z{T}_{pe}\end{array}|t-T_E|<T_{acq}/2\text{\hspace{1em}(5.111)}$$

其中 $G_x$ 为常数，但 $G_y=m\Delta G_y$ 且 $G_z=n\Delta G_z$。这里 $\bar{\gamma }$ 是旋磁比，$T_E$ 是回波时间，$T_{pe}$ 是相位编码时间，$T_{acq}$ 是数据采集时间窗。通过改变 $m$ 和 $n$ 的值，可以在 $k_y$-$k_z$ 平面内系统地遍历不同的相位编码步进，从而实现对三维k空间的均匀采样。

作为另一个示例，下图展示了另一种三维频率编码成像序列。

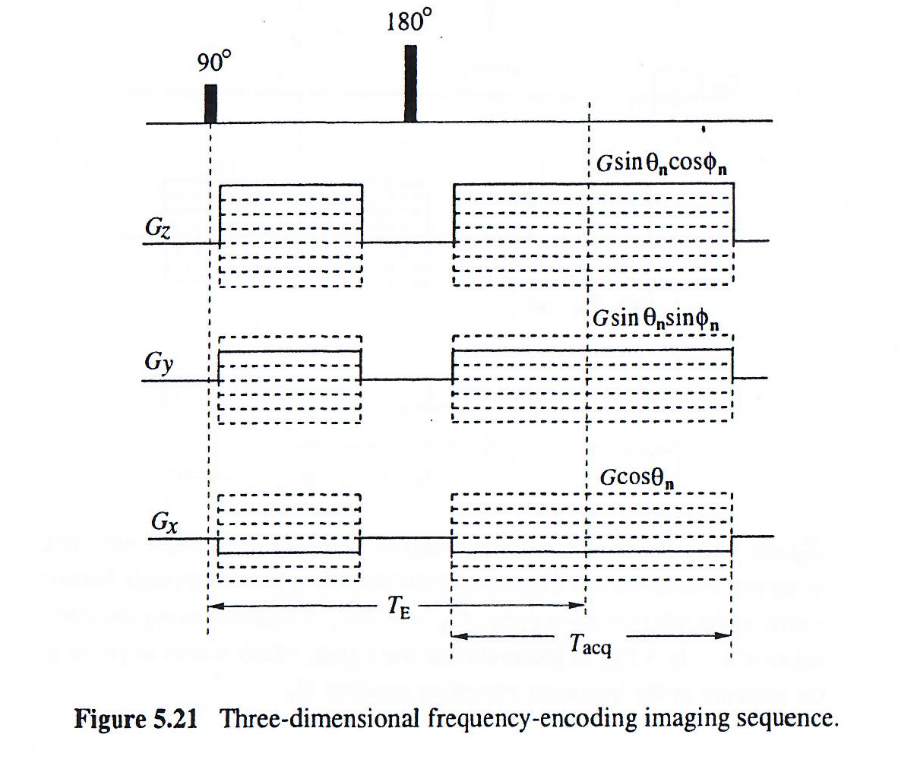
与上一个范例不同在于，$x,y,z$方向都是进行频率编码，$k$空间现在由通过原点的径向线填充。这可以通过注意每个频率编码信号的以下k空间采样轨迹方程来理解：
$$\{\begin{array}{l}{k}_x=\bar{\gamma }{G}_x(t-T_E)\\ k_y=\bar{\gamma }{G}_y(t-T_E)\\ k_z=\bar{\gamma }{G}_z(t-T_E)\end{array}|t-T_E|<T_{acq}/2\text{\hspace{1em}(5.112)}$$

其中 $G_x$、$G_y$ 和 $G_z$ 根据以下公式选择：
$$\{\begin{array}{l}{G}_x=G\sin {\theta }_n\cos {\varphi }_m\\ G_y=G\sin {\theta }_n\sin {\varphi }_m\\ G_z=G\cos {\theta }_n\end{array}\text{\hspace{1em}(5.113)}$$

其中 $G$ 是梯度幅值，${\theta }_n$ 和 ${\varphi }_m$ 分别表示极角和方位角。通过系统地改变这些角度，可以实现对三维$k$空间的径向采样模式。

上述讨论表明，三维成像的概念与二维成像没有太大不同。然而，三维成像确实呈现一些独特的实际问题，因为覆盖三维$k$空间需要更多编码次数。后续将讨论与有限数据采集时间、分辨率和信噪比相关的一些实际成像问题。