当前位置：首页 > news >正文

C++--二叉搜索树

news 2025/10/7 6:00:13

二叉搜索树的结构

insert插入

中序遍历

查找find

删除erase

key/value使用场景

二叉搜索树

什么是二叉搜索树？

左子树上所有节点的值都小于根，右子树上所有节点的值都大于根，它的左右子树也都是二叉搜索树

二叉搜索树的效率？

最好情况下，是一个完全二叉树，高度为log2 N；最差情况下，退化成一个单枝二叉树，高度为N

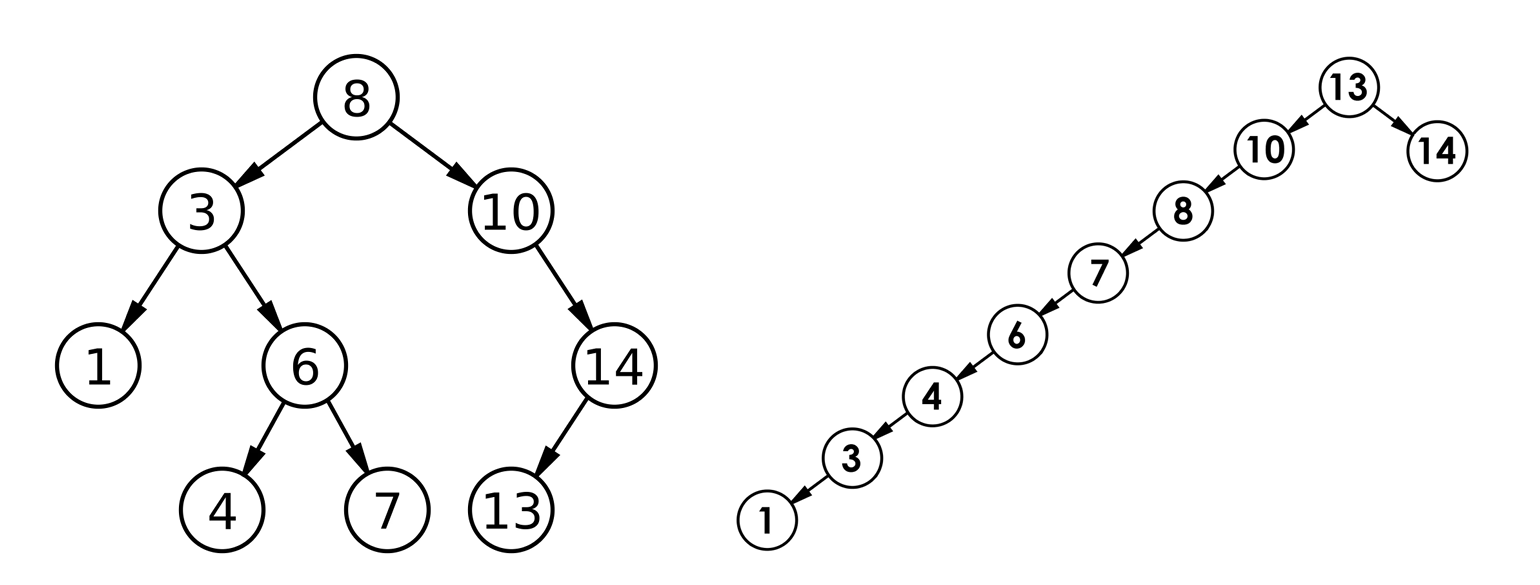
所以，二叉搜索树的增删查改效率为O（N）

二分查找也可以实现log2N的查找效率，但它有几个巨大的缺陷

要求存储在能进行下标随机访问的结构中，且必须有序
插入和删除的效率低，因为需要大量移动数据

二叉搜索树包括两个版本-冗余版本和非冗余版本

这里进行非冗余版本的介绍，即不允许存在值相等的节点，拒绝重复值

二叉搜索树的结构

template<class k>
struct BTNode
{BTNode(const k& key ):_key(key),_left(nullptr),_right(nullptr){}k _key;//关键字BTNode<k>* _left;BTNode<k>* _right;
};template<class k>
class BTree
{using Node = BTNode<k>;//C++11中的起别名，相当于typedef
private:Node* _root=nullptr;
};

insert插入

分两种情况

树为空，则创建一个值为key的新节点，将它赋给_root
树不为空，则要找到要插入节点的位置，插入值比当前值大的往左走，小的往右走

插入节点一定要和父亲链接上，所以要有一个parent指针

bool insert(const k& key)
{if (_root == nullptr){_root = new Node(key);return true;}//寻找插入位置Node* parent = _root;Node* cur = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;//相等则插入失败}//那我是插在parent的左边还是右边呢？if (key < parent->_key){parent->_left = new Node(key);}else// (key > parent->_key){parent->_right = new Node(key);}return true;
}

中序遍历

访问顺序：左子树->根->右子树，由于搜索二叉树的左>根>右，打印出来的一定是个严格递增的数列

利用递归

void _InOrder(Node* root)
{//递归的结束条件if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}

由于private，不能在外面访问_root

如果在主函数里面传参，BTree tree1；_InOrder(tree1->_root)，但是_root只能在类里面进行访问，在外面禁止访问，因此我们还要提供一个接口，InOrder。

void InOrder()
{_InOrder(_root);
}void _InOrder(Node* root)
{//递归的结束条件if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}

这样传参时只用调用 InOrder()，在内部自动调用_InOrder()

查找find

直接从根节点_root的值开始比较，如果key的值比当前节点的值大，那就往左走，比当前节点的值小，那就往右走，看走到空之前是否找到

（对于冗余版本，如果找到了则返回中序第一次出现的x）

bool Find(const k& key)
{Node* cur = _root;while (cur != nullptr){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}elsereturn true;}return false;//节点遍历完了还没找到
}

删除erase

1.删除叶子节点，直接给父亲打声招呼

2.删除非叶子节点有两种情况

a)这个节点有一个孩子，那就跟爹打声招呼，把娃交给你

b)这个节点有两个孩子，

将这个节点删除，那这个节点的父亲就要管理三个孩子，但这是一颗二叉树，因此我们得找一个节点来替代这个删除的节点，并且不能破坏这个二叉搜索树的结构，

这个替换的节点要满足，替换后的节点的值要大于这个位置的左子树的值，要小于这个位置的右子树的值。

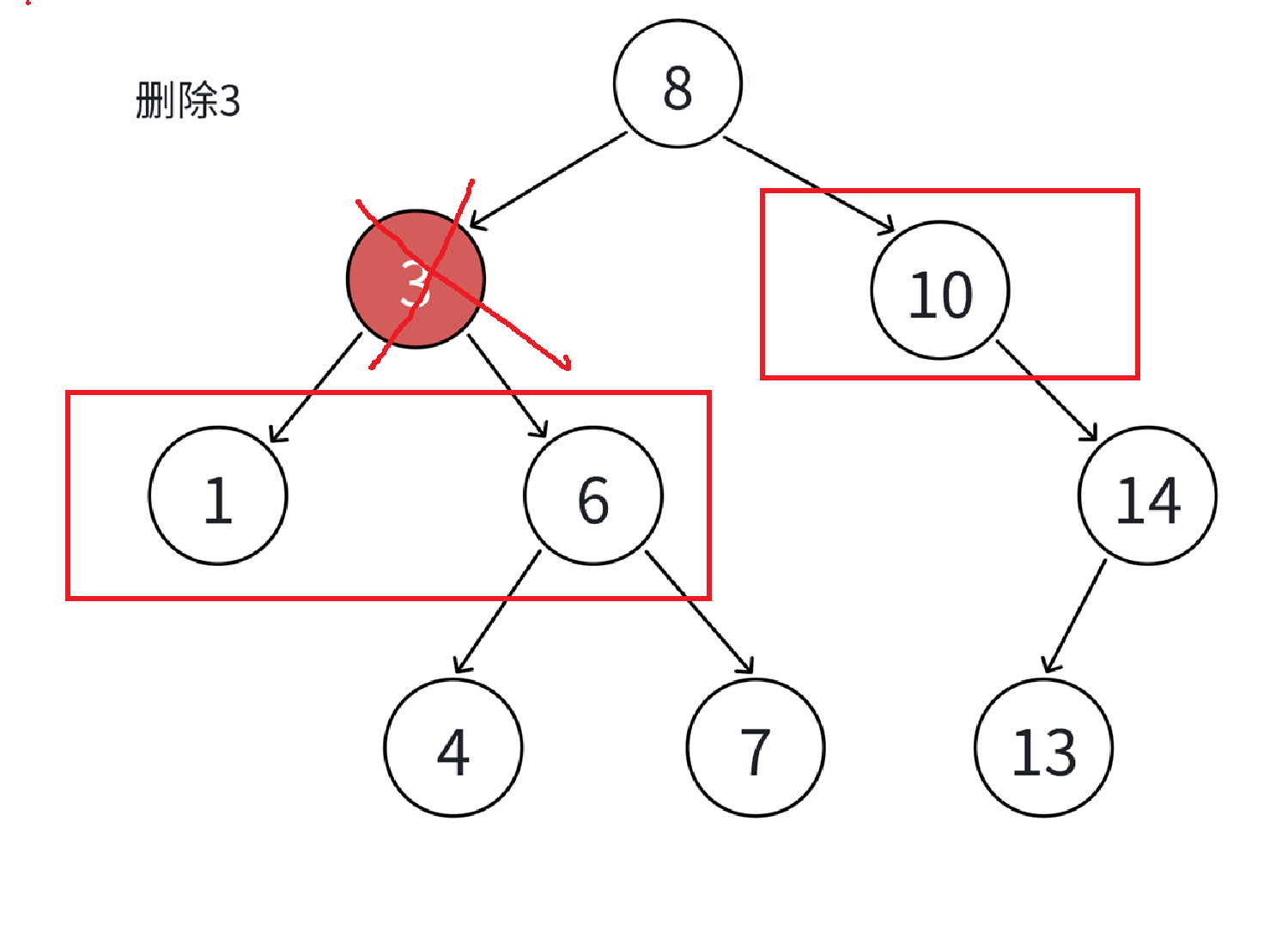
如何选择替换节点？

找这个待删除节点左子树的最大值（左子树最右侧的节点），因为这个待删除节点的左子树所有的值都<待删除节点的值<这个待删除节点的右子树的所有的值。那我们就找出左子树当中的最大值，来作为替换节点，它一定满足，小于待删除节点的右子树的所有的值，大于待删除节点的左子树所有的值。

或者，找这个待删除结点右子树的最小值（右子树最左侧的节点）。同理，这个替换节点一定满足，它是右子树当中最小的节点，是左子树当中最大的节点。

删除的第一步是查找，就是上文的find操作
删除之前需要给删除节点的父亲打声招呼，因此需要记录待删除节点的父亲
也要记录替换节点的父亲，因为替换节点也会有孩子，那就要将爷孙链接
而且要注意不要删除原节点，要删除替换节点，避免复杂的重新链接

bool Erase(const k& key)
{Node* parent = nullptr;Node* cur = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else//相等了 找到要删除的节点{//进行删除操作//首先我得确定这个待删除结点的孩子情况，是左孩子为空，还是右孩子为空，还是左右孩子都不为空if (cur->_left == nullptr)//删除节点的左孩子为空{if (cur == _root){_root = _root->_right;}//然后我得知道这个待删除的节点是父亲的左孩子还是右孩子，这样才能进行父亲和孙子的链接//前提，得有parentelse{if (parent->_left == cur)//带删除的节点是父亲的左孩子{//那父亲的左孩子就得指向待删除结点的右孩子parent->_left = cur->_right;}else//待删除节点是父亲的右孩子{//将父亲的右孩子指向待删除结点的右孩子parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//删除节点的右孩子为空{if (cur == _root){_root = _root->_left;}//判断删除节点是父节点的左还是右//前提，得有parentelse{if (parent->_left == cur)//带删除的节点是父亲的左孩子{//将父亲的左孩子指向待删除结点的左孩子parent->_left = cur->_left;}else//待删除的节点是父亲的右孩子{//将父亲的右孩子指向待删除结点的右孩子parent->_right = cur->_left;}}delete cur;}else//删除节点有两个孩子，{//接下来进行替换//找这个待删除结点左子树中的最大值，即最右侧的节点Node* replace = cur->_left;//记录替换节点的父亲，确保能将替换节点的孩子不丢失Node* replace_parent = cur;while (replace->_right != nullptr){replace_parent = replace;replace = replace->_right;}//replace现在为左子树最右侧的节点//将待删除结点的key替换成replace的keycur->_key = replace->_key;//接下来就要确定替换节点是父亲的左孩子还是右孩子if (replace_parent->_left == replace)//替换节点是其父亲的左孩子{replace_parent->_left = replace->_left;//将替换节点的父节点与替换节点的左孩子相连}else{replace_parent->_right = replace->_left;}//删除替换节点，而非原节点delete replace;}return true;}}return false;
}

二叉搜索树的删除算法面试常考

搜索二叉树不允许修改key，因为已有可能破坏这棵树的结构

key/value使用场景

比如通讯录，通过key找到“张三”，通过key找到value，value是电话号码，即key是索引关键字，value是内容，可以是任意类型

key是唯一标识，不支持修改，但value可以修改

再比如key是车牌号，value是车进入停车场的起始时间

在key的基础上改动：

在节点BTNode中新增一个成员变量value
在插入insert逻辑中，new(key,value)
find的返回值改为BTNode<k,v>*
erase中增加cur->value=replace->valus
中序遍历增加cur->value的打印

template<class k,class v>
struct BTNode
{BTNode(const k& key,const v& value):_key(key),_value(value), _left(nullptr), _right(nullptr){}k _key;//关键字v _value;BTNode<k, v>* _left;BTNode<k, v>* _right;
};
template<class k,class v>
class BTree
{using Node = BTNode<k, v>;//C++11中的起别名，相当于typedef
public:bool insert(const k& key,const v& value){if (_root == nullptr){_root = new Node(key, value);return true;}//寻找插入位置Node* parent = _root;Node* cur = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}//那我是插在parent的左边还是右边呢？if (key < parent->_key){parent->_left = new Node(key, value);}else {parent->_right = new Node(key, value);}return true;}BTNode<k,v>* Find(const k& key){Node* cur = _root;while (cur != nullptr){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}elsereturn cur;}return nullptr;//节点遍历完了还没找到}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){//递归的结束条件if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " " << root->_value;_InOrder(root->_right);}bool Erase(const k& key){Node* parent = nullptr;Node* cur = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else//相等了 找到要删除的节点{//进行删除操作//首先我得确定这个待删除结点的孩子情况，是左孩子为空，还是右孩子为空，还是左右孩子都不为空if (cur->_left == nullptr)//删除节点的左孩子为空{if (cur == _root){_root = _root->_right;}//然后我得知道这个待删除的节点是父亲的左孩子还是右孩子，这样才能进行父亲和孙子的链接//前提，得有parentelse{if (parent->_left == cur)//带删除的节点是父亲的左孩子{//那父亲的左孩子就得指向待删除结点的右孩子parent->_left = cur->_right;}else//待删除节点是父亲的右孩子{//将父亲的右孩子指向待删除结点的右孩子parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//删除节点的右孩子为空{if (cur == _root){_root = _root->_left;}//判断删除节点是父节点的左还是右//前提，得有parentelse{if (parent->_left == cur)//带删除的节点是父亲的左孩子{//将父亲的左孩子指向待删除结点的左孩子parent->_left = cur->_left;}else//待删除的节点是父亲的右孩子{//将父亲的右孩子指向待删除结点的右孩子parent->_right = cur->_left;}}delete cur;}else//删除节点有两个孩子，{//接下来进行替换//找这个待删除结点左子树中的最大值，即最右侧的节点Node* replace = cur->_left;//记录替换节点的父亲，确保能将替换节点的孩子不丢失Node* replace_parent = cur;while (replace->_right != nullptr){replace_parent = replace;replace = replace->_right;}//replace现在为左子树最右侧的节点//将待删除结点的key替换成replace的keycur->_key = replace->_key;cur->_value = replace->_value;//接下来就要确定替换节点是父亲的左孩子还是右孩子if (replace_parent->_left == replace)//替换节点是其父亲的左孩子{replace_parent->_left = replace->_left;//将替换节点的父节点与替换节点的左孩子相连}else{replace_parent->_right = replace->_left;}//删除替换节点，而非原节点delete replace;}return true;}}return false;}private:Node* _root = nullptr;
};

查看全文

http://www.dtcms.com/a/449426.html