当前位置：首页 > news >正文

随机试验中异质性处理效应的通用机器学习因果推断

news 2025/10/6 8:56:59

“机器学习”与“因果推断”的联姻：解密异质性效应的通用框架

Chernozhukov V, Demirer M, Duflo E, et al. Fisher–Schultz lecture: Generic machine learning inference on heterogeneous treatment effects in randomized experiments, with an application to immunization in India[J]. Econometrica, 2025, 93(4): 1121-1164.

在数据科学日新月异的今天，“机器学习”（Machine Learning, ML）无疑是风头最盛的“预测革命”的旗手，而“随机对照试验”（Randomized Controlled Trials, RCT）则是经济学、医学和社会科学领域“可信度革命”的基石。前者擅长从高维数据中挖掘复杂的预测模式，后者则为我们提供了评估干-预措施因果效应的黄金标准。乍看之下，两者似乎分属不同领域，但当它们交汇时，便能迸发出巨大的能量，尤其是在探索一个核心问题上：一项政策或干预措施，对不同的人群会产生怎样不同的效果？

这就是“异质性处理效应”（Heterogeneous Treatment Effects, HTE）分析。理解异质性至关重要——它能帮助我们优化资源配置，将政策精准地投向最需要或最能受益的人群，并深化我们对政策作用机制的理解。然而，探索异质性的过程也充满了陷阱。研究者往往拥有大量的个体特征数据（协变量），如果随意地在事后根据这些特征划分亚组、比较效应，极易陷入“数据挖掘”或“p值 hacking”的泥潭，得出看似显著实则虚假的结论。事实上，一篇对经济学顶级期刊的综述发现，40%的RCT论文都进行了亚组分析，这凸显了对纪律性方法的迫切需求。

为了在探索异质性时维持科学的严谨性，Victor Chernozhukov, Mert Demirer, Esther Duflo和Iván Fernández-Val在Econometrica上发表的这篇前沿论文中，提出了一个通用的、稳健的、且对机器学习方法“不可知”（agnostic）的推断框架。这个框架旨在系统性地利用任何机器学习工具来发现和量化异质性效应，同时避免过度拟合，并提供有效的统计推断。

核心挑战与“不可知”的务实方法

高维推断的根本困境

在高维数据环境下，直接精确估计每个个体真实的"条件平均处理效应"（Conditional Average Treatment Effect, CATE）函数——即s₀(Z)，一个基于个体特征Z的复杂函数——是一项极其艰巨甚至不可能完成的任务。这背后是统计学中著名的"维度灾难"（curse of dimensionality）。

Stone (1982) 的经典理论结果表明了这一困境的严重性：如果协变量Z的维度为d，目标函数s₀(Z)假设具有p个连续有界导数，那么从大小为N的随机样本中学习这个函数的最坏情况（minimax）下界不能优于N^(-p/(2p+d))当N → ∞时。因此，如果p固定且d也较小但随N缓慢增长（如d ≥ log N），那么一般来说不存在s₀(Z)的一致估计量。这意味着，在没有强假设的情况下，通用的机器学习估计器无法被视为一致的。

稀疏性假设的两难

机器学习方法通过有效探索各种形式的"稀疏性"来产生对s₀(Z)的"良好"近似。最简单的稀疏性形式是假设s₀(Z)可以被一个仅依赖于Z的低维子集的函数很好地近似，从而使一致估计成为可能。在稀疏性假设下，这些方法在高维设置中的表现可以远超经典方法。

然而，稀疏性或更一般地说CATE函数s₀的低复杂性，都是不可检验的假设，必须谨慎使用。没有某种形式的稀疏性，获得s₀(Z)的一致估计器是困难的，甚至是不可能的。这在理论与实践之间造成了巨大的鸿沟。

"不可知论"的务实转向

面对这一根本性难题，作者们采取了一种非常务实的"不可知论"策略。正如论文所述：“我们既不依赖任何稀疏性或低复杂性假设来使ML估计器一致，也不施加其他更强的条件来使’传统’置信区间有效。我们简单地将ML视为为感兴趣的对象提供代理预测器。”

这种方法的核心思想是：我们不必追求完美估计CATE函数本身，而是退一步，专注于对CATE的几个关键特征进行有效估计和稳健推断。 通过关注更粗糙的对象而非函数本身，但尽可能少地做假设，这似乎是一个值得的牺牲。

样本分割的两阶段策略

该框架通过以下两步实现，其关键在于样本分割（sample splitting）：

第一阶段：在辅助样本中生成"代理预测器"

设(M, A)表示指标集{1, ..., N}的随机划分。我们将数据Data = (Y_i, D_i, Z_i)_{i=1}^N随机分割为：

主样本（Main Sample）：Data_M = (Y_i, D_i, Z_i)_{i∈M}
辅助样本（Auxiliary Sample）：Data_A = (Y_i, D_i, Z_i)_{i∈A}

在辅助样本上，研究者可以自由地使用任何偏爱的机器学习方法来训练模型。这些ML方法可以包括：

惩罚化方法（如Lasso、Ridge）
神经网络
随机森林
提升树（Boosted Trees）
集成方法（Ensemble Methods）

这些方法既可以是预测型的（直接预测结果Y），也可以是因果型的（直接针对处理效应设计）。无论使用哪种方法，产生的预测值S(Z)都被视为真实CATE s₀(Z)的一个"代理"或"替身"，我们不要求它完美或无偏。

第二阶段：在主样本上进行后处理和推断

将第一阶段训练好的模型应用到主样本上，为每个观测值生成代理预测值S(Z)。关键点在于：由于S(Z)是在与主样本数据完全独立的辅助样本上训练的，这就从根本上避免了过度拟合问题。在主样本看来，S(Z)只是一个固定的、预先给定的特征，统计推断因此回归到经典的线性回归和样本均值推断。

接着，在主样本上，我们不再关注S(Z)本身，而是基于它来估计CATE的三个关键特征。

异质性分析的三大支柱：BLP, GATES, 和 CLAN

作者们提出了三个核心的分析工具，它们共同构成了对异质性效应的全面解读。

1. 最佳线性预测器 (Best Linear Predictor, BLP)

BLP的理论基础与识别策略

机器学习直接给出的代理预测值S(Z)可能包含噪声，也可能存在系统性偏差。BLP的作用就是对这个原始的ML预测进行"校准"和"去噪"。从理论上讲，BLP是真实CATE s₀(Z)在给定S(Z)条件下的最佳线性预测：

$BLP[s0(Z)∣S(Z)]=β1+β2(S(Z)−E[S(Z)])\mathsf{BLP}[s_0(Z)|S(Z)] = \beta_1 + \beta_2 (S(Z) - \mathbb{E}[S(Z)])$

其中：
$β1=E[s0(Z)],β2=Cov(s0(Z),S(Z))Var(S(Z))\beta_1 = \mathbb{E}[s_0(Z)], \quad \beta_2 = \frac{\text{Cov}(s_0(Z), S(Z))}{\text{Var}(S(Z))}$

两种识别策略

论文提出了两种估计BLP参数的策略，它们在理论上是一阶等价的：

策略A：加权残差法（Weighted Residual）

该策略基于加权最小二乘回归：
$(Yi−b^(Zi))=β1+β2(S(Zi)−Sˉ)+ϵi(Y_i - \hat{b}(Z_i)) = \beta_1 + \beta_2(S(Z_i) - \bar{S}) + \epsilon_i$

其中权重为w(Z_i) = 1/[\hat{p}(Z_i)(1-\hat{p}(Z_i)))]，\hat{p}(Z)和\hat{b}(Z)分别是倾向得分和基线结果函数的估计。

策略B：Horvitz-Thompson变换法

该策略利用Horvitz-Thompson变换H_i = D_i/\hat{p}(Z_i) - (1-D_i)/(1-\hat{p}(Z_i))，它具有重要性质：
$E[YiHi∣Zi]=s0(Zi)\mathbb{E}[Y_i H_i | Z_i] = s_0(Z_i)$

即变换后的响应Y_i H_i提供了关于CATE的无偏信号。然后在变换后的变量上进行线性投影：
$YiHi−b^(Zi)Hi=β1+β2(S(Zi)−Sˉ)+ϵiY_i H_i - \hat{b}(Z_i)H_i = \beta_1 + \beta_2(S(Z_i) - \bar{S}) + \epsilon_i$

参数的经济学解释

这个线性关系中的两个系数具有非常直观的经济学含义：

β₁：代表了总体的平均处理效应（ATE），即β₁ = E[s₀(Z)]。
β₂：被称为**“异质性载荷”（heterogeneity loading）**，它衡量了ML代理S(Z)与真实CATE之间的关联强度：
- 如果β₂ = 0，说明S(Z)与真实效应无关，即我们未能通过该ML模型发现任何有意义的异质性。
- 如果β₂显著不为0，则证明了异质性的存在，并且我们使用的ML模型成功地捕捉到了它。
- 如果β₂接近1，说明ML代理的"校准"程度很好，它本身就是对CATE的一个不错的无偏预测。
- β₂的符号告诉我们ML预测的方向是否正确：正值意味着ML正确识别了效应的相对大小。

因此，检验β₂是否为零，就成了我们检验异质性是否存在的一个严谨方法。这个检验的零假设是"不存在异质性"，备择假设是"存在异质性且ML模型捕捉到了它"。

BLP的去噪效果

论文中的模拟清晰地展示了BLP的威力：

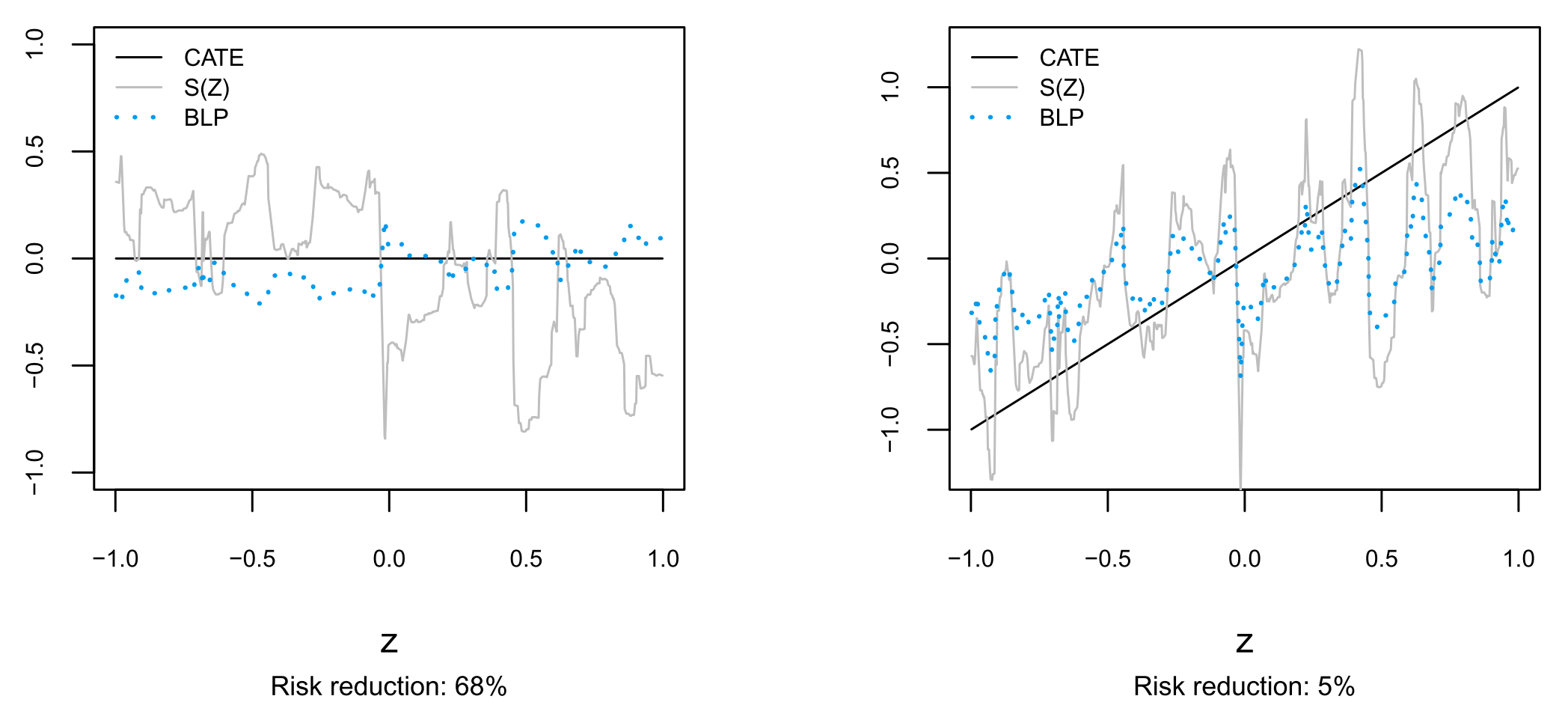
图1：BLP的去噪效果。左图：当真实效应为零时，原始的ML代理（浅灰线）充满了噪声，而BLP（虚线）成功地将其拉回零线附近，风险降低了68%。右图：当存在真实异质性时，BLP依然能平滑ML代理，降低5%的风险。

2. 分组平均处理效应 (Sorted Group Average Treatment Effects, GATES)

GATES的核心思想与实现

GATES可能是整个框架中最直观、对政策制定者最友好的工具。它将复杂的异质性模式转化为简单易懂的分组比较。

实现步骤：

排序：利用ML代理S(Z)对主样本中的所有个体进行排序，从预测效应最低的到最高的。
分组：将排序后的个体分成K个组（通常K=5，每组占20%的人群）。设G_k表示第k个组的指示变量。
估计：分别计算每个组内的平均处理效应。

两种估计策略

与BLP类似，GATES也有两种对应的估计策略：

策略A：加权残差GATES
$(Yi−b^(Zi))=∑k=1KγkGk,i+ϵi(Y_i - \hat{b}(Z_i)) = \sum_{k=1}^K \gamma_k G_{k,i} + \epsilon_i$
使用权重w(Z_i)进行加权最小二乘估计。

策略B：Horvitz-Thompson GATES
$YiHi−b^(Zi)Hi=∑k=1KγkGk,i+ϵiY_i H_i - \hat{b}(Z_i)H_i = \sum_{k=1}^K \gamma_k G_{k,i} + \epsilon_i$

其中γ_k就是第k组的GATES估计，代表该组的平均处理效应。

GATES的政策价值

通过比较不同组别的效应大小，我们可以清晰地看到：

谁从政策中获益最多：通常是γ_K（最高预测效应组）
谁获益最少：通常是γ_1（最低预测效应组）
是否存在负面效应：如果某些γ_k < 0
效应的分布形状：线性递增、凸性、凹性等

这为政策的精准定位提供了直接的证据。例如，如果γ_5 >> γ_4 > γ_3 > γ_2 > γ_1，说明政策应该优先投向预测效应最高的20%人群。

统计检验

GATES还允许进行多种有意义的假设检验：

单调性检验：H₀: γ₁ = γ₂ = ... = γ_K（无异质性）
线性性检验：效应是否随组别线性变化
凸性/凹性检验：边际效应是否递增或递减

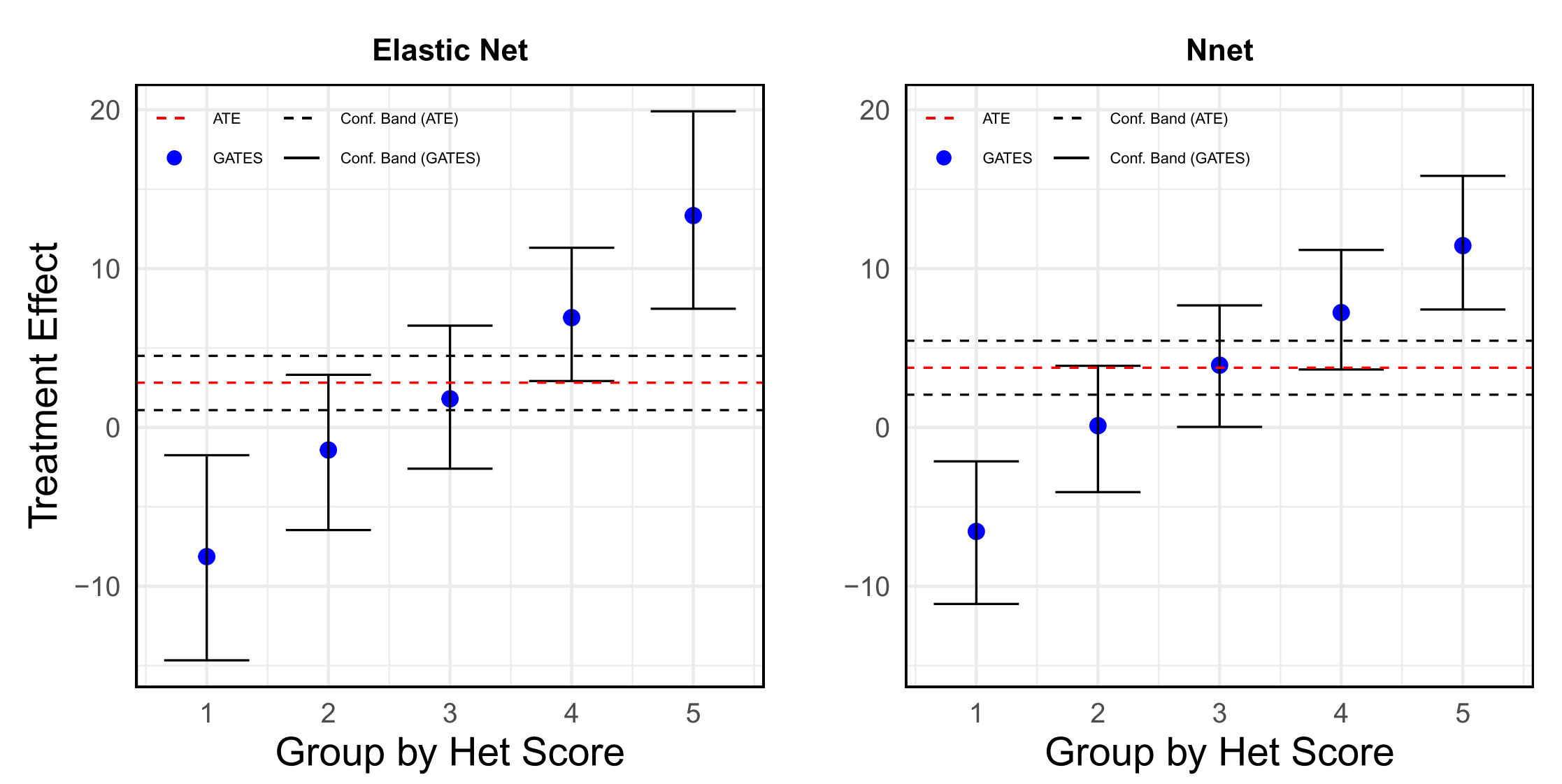
图2：GATES分析示意图。此图展示了按预测效果分成的五组人群的平均处理效应，清晰地揭示了巨大的异质性。

3. 分类分析 (Classification Analysis, CLAN)

CLAN的目标与方法

在通过GATES确定了"最受影响"和"最不受影响"的群体后，一个自然而然的问题是：这两个极端群体究竟有什么不同？ CLAN就是用来回答这个问题的。

CLAN的核心思想是通过比较极端群体（通常是G₁组和G_K组）在基线特征上的差异，来识别那些能够预测处理效应大小的可观测特征。

实现方法

设Z_j表示第j个基线特征（j = 1, ..., p），CLAN估计以下差异：

$δj=E[Zj∣GK]−E[Zj∣G1]\delta_j = \mathbb{E}[Z_j | G_K] - \mathbb{E}[Z_j | G_1]$

即最高效应组与最低效应组在特征j上的平均差异。

统计推断：对每个特征，我们可以检验：

H₀: δⱼ = 0（该特征在两组间无差异）
H₁: δⱼ ≠ 0（该特征是异质性的预测因子）

CLAN的政策价值

通过CLAN，我们可以：

为不同群体画像：识别高效应群体和低效应群体的典型特征
发现可操作的定位指标：找到可以在现实中用于识别目标人群的简单特征
理解作用机制：通过特征差异推断政策为何对某些群体更有效
指导政策设计：为未来的政策干预提供精准定位的依据

例如，如果CLAN发现高效应组的特征是"基线免疫率低、收入水平低、教育程度低"，那么政策制定者就可以将资源优先投向具有这些特征的社区。

多重检验问题

由于CLAN涉及对多个特征的同时检验，需要控制多重检验的错误率。论文采用了适当的多重检验校正方法，如Bonferroni校正或FDR控制，以确保发现的显著特征是真实的而非偶然的。

应对不确定性：多重分割与分位数聚合

单次分割的局限性

仅仅依赖一次随机的数据分割是有风险的——结果可能只是特定分割下的巧合。虽然条件于单次数据分割的统计推断在概念上是直接且吸引人的（因为它将统计推断简化为经典的线性回归和样本均值推断），但这引入了来自特定数据分割随机抽取的额外变异性。

多重分割策略

为了确保结果的稳健性，作者们提出了一套基于**多重样本分割（multiple sample splits）和分位数聚合（quantile aggregation）**的推断方法。

具体实施：

重复分割：研究者重复整个流程（从分割数据到计算BLP、GATES、CLAN）成百上千次。论文中使用了B = 250次分割。
独立估计：对于每次分割b = 1, ..., B，我们得到：
- BLP参数的估计：β₁^(b), β₂^(b)
- GATES估计：γ₁^(b), ..., γ_K^(b)
- CLAN估计：δ₁^(b), ..., δ_p^(b)
- 对应的置信区间和p值
分位数聚合：对于每个目标参数，我们都会得到一个由250个估计值构成的分布。

聚合规则

点估计：
$θ^=median{θ^(1),...,θ^(B)}\hat{\theta} = \text{median}\{\hat{\theta}^{(1)}, ..., \hat{\theta}^{(B)}\}$

置信区间：设CI^(b) = [L^(b), U^(b)]为第b次分割得到的置信区间，则最终的置信区间为：
$[\text{median}\{L^{(1)}, ..., L^{(B)}\}, \text{median}\{U^{(1)}, ..., U^{(B)}\}]$

p值：
$\text{median}\{p^{(1)}, ..., p^{(B)}\}$

理论保证

这种聚合方法具有重要的理论性质：

渐近有效性：在适当的正则性条件下，聚合后的置信区间保持渐近有效的覆盖率。
稳健性：中位数聚合对异常分割具有稳健性，避免了个别"坏"分割对结果的过度影响。
可重复性：不同研究者使用相同方法得到的结果具有更高的一致性。

这种聚合方法极大地降低了由单次数据分割带来的随机性风险，使得最终的结论更加可靠和可重复。

更进一步：构建直接学习CATE的"因果机器"

从预测学习到因果学习的范式转换

传统的机器学习模型，其目标是最小化对结果Y的预测误差。然而，在因果推断的场景下，我们真正关心的是处理效应s₀(Z)。这两个目标之间存在根本性的差异：预测Y需要学习E[Y|D,Z]，而估计CATE需要学习E[Y|D=1,Z] - E[Y|D=0,Z]。

论文指出，我们可以通过改造机器学习算法的损失函数（loss function），使其直接优化对CATE的拟合，从而构建出更强大的"因果学习器"（Causal Learners）。

神谕性质的损失函数

作者提出了两种基于"加权残差"和"Horvitz-Thompson变换"的新损失函数。这些损失函数被巧妙地设计出来，使得最小化它们等价于最小化 E[(s₀(Z) - S(Z))²]，即代理S(Z)与真实CATEs₀(Z)之间的均方误差。这是一种"神谕"（oracle）性质，因为它让我们可以直接优化一个我们本来看不见的目标。

加权残差学习器 (WR Learner)

目标函数A：
$min⁡b,sE[w(Z)⋅(Y−b(Z)−(D−p(Z))s(Z))2]\min_{b,s} \mathbb{E}[w(Z) \cdot (Y - b(Z) - (D - p(Z))s(Z))^2]$

其中：

w(Z) = 1/[p(Z)(1-p(Z))] 是逆方差权重
b(Z) 是基线函数的估计
s(Z) 是我们要学习的CATE函数

神谕性质：在真实的p(Z)和b(Z)已知的情况下，最小化上述目标函数等价于最小化 $E [(s_{0} (Z) - s (Z))^{2}]$ 。

HT学习器 (HT Learner)

目标函数B：
$min⁡b,sE[(YH−b(Z)H−s(Z))2]\min_{b,s} \mathbb{E}[(YH - b(Z)H - s(Z))^2]$

其中H = D/p(Z) - (1-D)/(1-p(Z))是Horvitz-Thompson变换。

神谕性质：同样，在真实的nuisance参数已知时，最小化此目标函数也等价于最小化 $E [(s_{0} (Z) - s (Z))^{2}]$ 。

实际实现：因果提升算法

在实践中，论文通过**提升（boosting）**方法来实现这些因果学习器。算法的基本思路是：

初始化：从一个预测型学习器开始（如标准的随机森林）
因果提升：寻找相对简单的偏离，以改进CATE预测
迭代优化：通过多轮提升来逐步改进

这种方法之所以有效，是因为目标函数(A)和(B)往往比预测学习中的目标函数更加嘈杂且难以调优，直接求解大参数空间上的目标函数效果不佳。

理论优势与实证表现

使用这些损失函数训练的ML模型，从一开始就以捕捉因果效应为目标，而不是预测。理论和实践都证明：

更准确的CATE逼近：因果学习器能更准确地逼近真实的CATE函数
更好的BLP性能：在BLP分析中，因果学习器通常产生更接近1的β₂值
更清晰的GATES模式：在GATES分析中，异质性模式更加明显

特别地，论文的模拟显示，因果提升可以将因果森林的RMSE改进54%-63%。

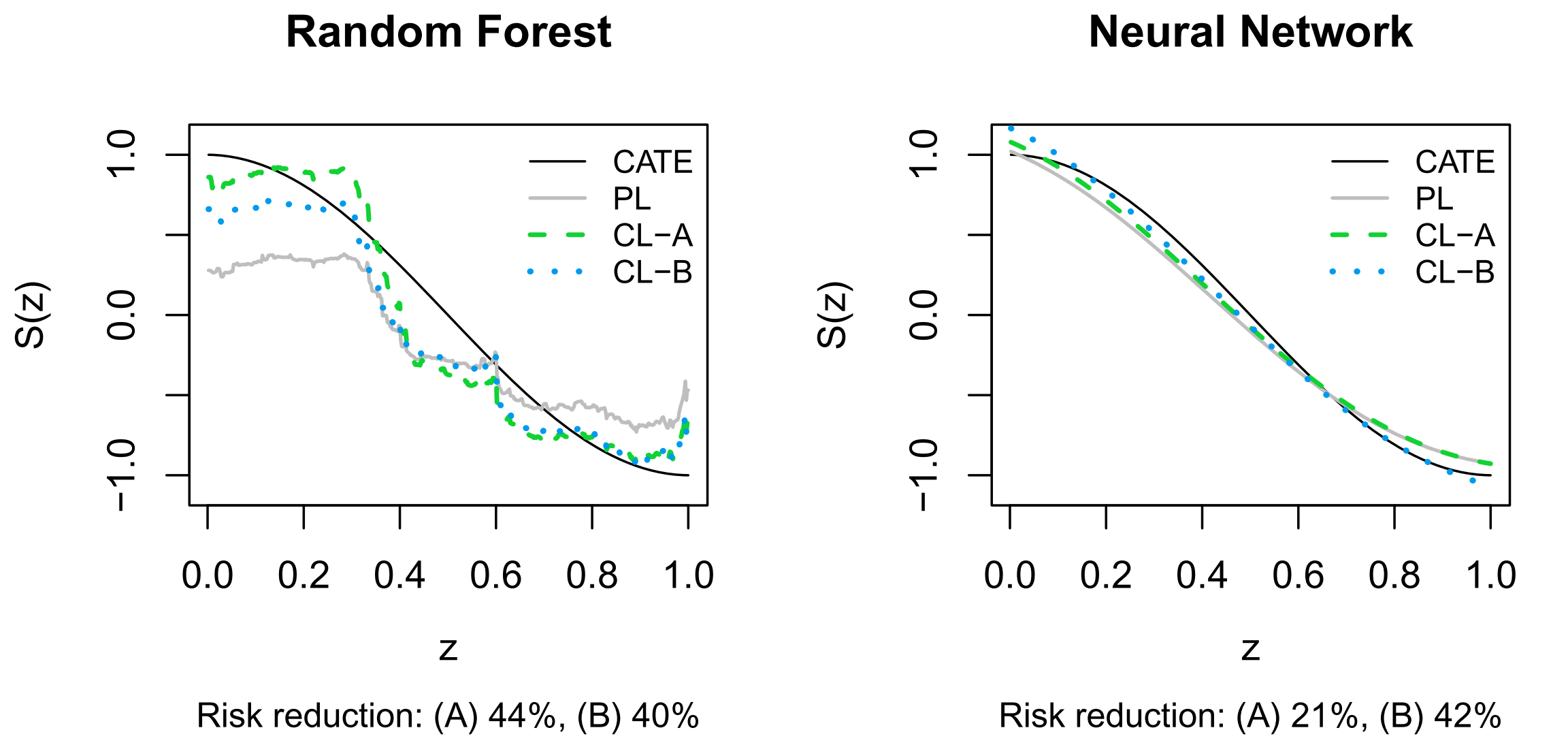
图3：预测型学习器 vs. 因果学习器。实线为真实CATE，浅灰色线为标准ML（预测型）的估计，虚线和点线为两种因果学习器的估计。可见因果学习器能更好地拟合真实的CATE曲线。

实证应用：印度免疫接种激励计划

实验背景与政策重要性

理论的价值最终要在实践中体现。论文将这一整套框架应用于一个在印度哈里亚纳邦进行的大规模RCT项目，这是Banerjee等人(2019)设计和实施的重要实验。

全球免疫接种挑战：免疫接种被普遍认为是预防疾病、残疾和死亡最有效和最具成本效益的方式之一。然而，全世界每年仍有近2000万儿童无法接受关键的免疫接种。虽然早期政策努力主要集中在改善免疫接种服务的基础设施上，但最近的文献表明，"助推"措施（如小额激励、利用社交网络、短信提醒、社会信号等）可能对这些服务的使用产生巨大影响。

实验设计与规模

这是一个与哈里亚纳邦政府合作的大规模实验，政府愿意尝试各种助推措施的组合，目标是选择最有效的政策并大规模实施。实验建立了一个定制的疫苗接种平台，规模包括：

地理覆盖：7个区县，140个初级卫生中心
村庄数量：2360个村庄参与实验（包括915个面临所有处理的村庄）
儿童数量：结果数据库中有295,038名儿童
实验设计：村庄级别的交叉随机化设计

基线情况的严峻性

实验开始时的免疫接种情况非常严峻：

在该地区的每个村庄中，父母报告孩子接受麻疹疫苗（序列中的最后一个）的儿童比例仅为39%
只有**19.4%**的儿童在15个月前接受了疫苗，而完整的接种序列应该在一年内完成
这种低接种率凸显了政策干预的迫切需要

三大助推措施

实验采用了三种主要的助推措施的交叉随机化设计：

提供激励：为按时接种的家庭提供小额经济激励
发送短信提醒：通过SMS系统提醒家长接种时间
播种大使：在社区中培养免疫接种的倡导者

每种政策都包含多个变体（如激励水平的不同、短信提醒覆盖程度的不同），使得政策组合空间非常复杂。

研究的独特挑战

这是一个完美的应用场景，体现了本文方法的价值：

高维政策空间：多种政策的不同变体组合产生了复杂的处理空间
成本考虑：政府推出的"激励+动员+提醒"组合方案成本不菲，因此迫切希望知道这个方案在哪些村庄最有效
先验知识缺乏：在实验前，研究者对于哪些村庄特征会影响政策效果并没有强烈的先验知识
政策相关性：需要为政府提供可操作的、基于证据的政策建议

前分析计划的局限

实验的前分析计划规定要"按性别和村庄级别基线/全国人口普查变量（包括资产、信念、知识和对免疫接种的态度）寻找异质性"，但没有确定一两个具体的基线变量来关注。这反映了真正的不确定性（这种情况经常出现）。许多因素都可能影响政策影响，从态度到实施能力再到基线水平，研究者并没有关于在哪里寻找的具体理论。这正是需要原则性方法来避免过度拟合并提供政策相关建议的情境类型。

数据与变量

结果变量：Y是给定月份给定村庄中15个月或更小的儿童接受麻疹疫苗的数量。

处理变量：D是家庭所在村庄接受政策的指示变量。

协变量：Z包括36个基线村庄级别特征，如宗教、种姓、经济状况、婚姻和家庭状况、教育以及基线免疫接种情况。

倾向得分：在这个RCT中，倾向得分是常数（随机分配）。

主要研究发现

1. 强烈的异质性效应（BLP分析）

BLP分析提供了异质性存在的第一个强有力证据：

异质性载荷：β₂的估计值为1.047（标准误0.48），显著为正且接近1
平均处理效应：β₁约为每月增加2.8名儿童接种
统计显著性：β₂的p值远小于0.05，强烈拒绝"无异质性"的零假设

β₂接近1这一发现特别重要，它表明机器学习代理不仅捕捉到了异质性，而且校准得相当好，几乎可以直接用作CATE的无偏预测器。

2. 极端的效应分化（GATES分析）

GATES分析揭示了令人震惊的政策效应分化：

组别	描述	效应估计	置信区间
G1	最低预测效应组(20%)	-8.00	[-12.5, -3.5]
G2	低预测效应组(20%)	-2.15	[-6.2, 1.9]
G3	中等预测效应组(20%)	3.42	[-0.3, 7.1]
G4	高预测效应组(20%)	8.95	[4.8, 13.1]
G5	最高预测效应组(20%)	13.23	[8.7, 17.8]