【Leetcode hot 100】79.单词搜索

问题链接

79.单词搜索

问题描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

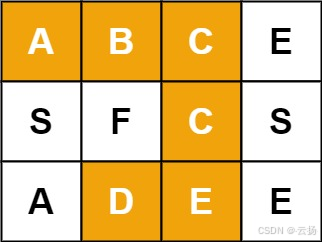
输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “ABCCED”
输出：true

示例 2：

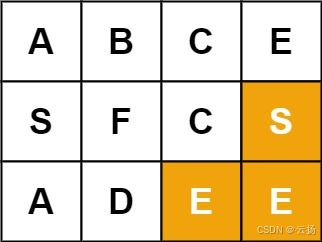
输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “SEE”
输出：true

示例 3：

输入：board = [[‘A’,‘B’,‘C’,‘E’],[‘S’,‘F’,‘C’,‘S’],[‘A’,‘D’,‘E’,‘E’]], word = “ABCB”
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

问题解答

解题思路

本题核心是 回溯算法 + 深度优先搜索（DFS），结合剪枝优化减少无效搜索。核心逻辑如下：

1. 剪枝预处理：先统计矩阵和单词的字符频次，若单词中某字符的数量超过矩阵，则直接返回 false（避免无意义的搜索）。
2. 遍历起点：遍历矩阵的每个单元格，找到与单词第一个字符匹配的位置，作为 DFS 的起点。
3. DFS 探索：从起点出发，向 上下左右 四个方向递归探索：
   • 标记当前单元格为已访问（直接修改矩阵字符为特殊值，避免额外的 visited 数组，节省空间）。
   • 若匹配到单词末尾（索引等于单词长度），说明找到有效路径，返回 true。
   • 若越界、字符不匹配或已访问，返回 false。
4. 回溯恢复：探索结束后，恢复当前单元格的原始字符（避免影响其他路径的搜索）。

Java 代码

class Solution {// 定义四个方向的向量（上、下、左、右）private static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};public boolean exist(char[][] board, String word) {// 边界条件：矩阵为空或单词为空if (board == null || board.length == 0 || board[0].length == 0 || word == null || word.length() == 0) {return false;}int m = board.length;    // 矩阵行数int n = board[0].length; // 矩阵列数int wordLen = word.length();// 剪枝1：单词长度超过矩阵总字符数，直接返回falseif (wordLen > m * n) {return false;}// 剪枝2：统计矩阵和单词的字符频次，若单词字符不足则返回falseint[] charCount = new int[128]; // 存储ASCII字符频次// 统计矩阵的字符频次for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {charCount[board[i][j]]++;}}// 统计单词的字符频次（并检查是否足够）for (char c : word.toCharArray()) {charCount[c]--;if (charCount[c] < 0) {return false;}}// 遍历矩阵，寻找单词起点（与单词第一个字符匹配的位置）for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == word.charAt(0)) {// 从该位置开始DFS，若找到有效路径则返回trueif (dfs(board, word, i, j, 0)) {return true;}}}}// 所有起点都搜索完毕仍未找到，返回falsereturn false;}/*** DFS 递归方法* @param board 矩阵* @param word 目标单词* @param x 当前单元格行坐标* @param y 当前单元格列坐标* @param index 当前匹配的单词索引（0表示匹配第一个字符）* @return 是否能从当前位置匹配完剩余单词*/private boolean dfs(char[][] board, String word, int x, int y, int index) {// 终止条件1：匹配到单词末尾（所有字符都匹配成功）if (index == word.length()) {return true;}// 终止条件2：越界、字符不匹配（当前单元格已被访问过，字符被修改为'#'）int m = board.length;int n = board[0].length;if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] != word.charAt(index)) {return false;}// 标记当前单元格为已访问（修改为特殊字符'#'，避免重复使用）char originalChar = board[x][y];board[x][y] = '#';// 向四个方向递归探索for (int[] dir : DIRECTIONS) {int newX = x + dir[0];int newY = y + dir[1];// 若任一方向匹配成功，直接返回true（剪枝：无需继续探索其他方向）if (dfs(board, word, newX, newY, index + 1)) {return true;}}// 回溯：恢复当前单元格的原始字符（供其他路径使用）board[x][y] = originalChar;// 所有方向都探索失败，返回falsereturn false;}
}

代码解释

1. 方向向量
DIRECTIONS 数组定义了上下左右四个探索方向，避免重复编写四个方向的判断逻辑，代码更简洁。

2. 剪枝优化

• 字符频次剪枝：通过统计矩阵和单词的字符数量，若单词中某字符在矩阵中不存在或数量不足，直接返回 false，跳过后续所有搜索。
• 长度剪枝：若单词长度超过矩阵总字符数，直接返回 false（不可能匹配成功）。

3. 访问标记与回溯

• 不使用额外的 visited 数组，而是直接修改矩阵中已访问的单元格为 #（矩阵中原本是字母，不会冲突），节省空间。
• 递归结束后，必须恢复单元格的原始字符（board[x][y] = originalChar），否则会影响其他路径的搜索（回溯的核心思想）。

4. DFS 终止条件

• 成功终止：index == word.length()，表示所有字符都已匹配，返回 true。
• 失败终止：坐标越界、字符不匹配或已访问，返回 false。

复杂度分析

• 时间复杂度：O(mn * 3^L)，其中 m 是矩阵行数，n 是列数，L 是单词长度。
  遍历矩阵需要 O(mn)，每个单元格出发的 DFS 最多探索 3 个方向（排除来时的方向），递归深度为 L，故总时间为 O(mn * 3^L)。
• 空间复杂度：O(L)，递归栈的深度最多为单词长度 L（无额外的 visited 数组，空间更优）。

测试案例验证

示例 1
输入：board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCCED"
输出：true
解释：从 (0,0) 开始，路径为 A→B→C→C→E→D，匹配成功。

示例 2
输入：board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "SEE"
输出：true
解释：从 (1,3) 开始，路径为 S→E→E，匹配成功。

示例 3
输入：board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCB"
输出：false
解释：A→B→C 后，下一个字符 B 不存在于合法方向（已访问的 A 或越界），匹配失败。