网站兼容性代码wordpress模版怎么上传

解析 LeetCode 46. 全排列：回溯算法的经典实践

在算法的奇妙世界中，LeetCode 46. 全排列问题是回溯算法的典型应用场景。该问题要求生成一个不含重复数字的数组的所有可能全排列，核心在于利用回溯思想遍历所有元素的排列组合。

一、题目分析

（一）问题定义

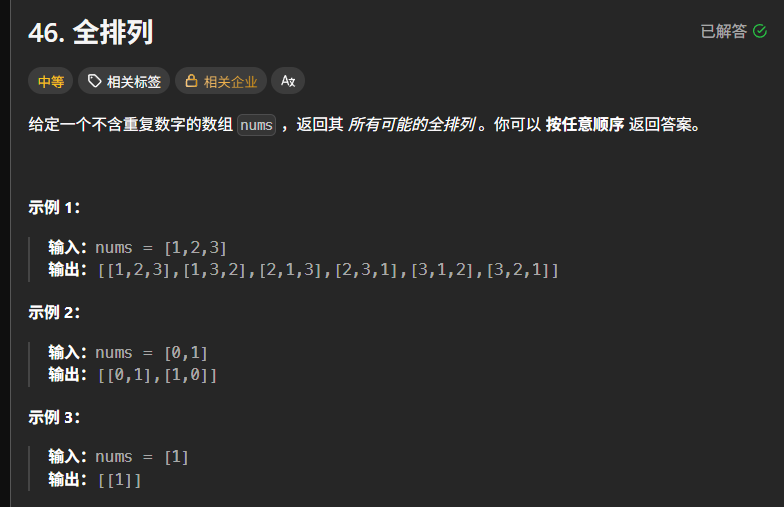
给定一个不含重复数字的整数数组 nums，返回其所有可能的全排列。例如，nums = [1,2,3] 时，输出应包含 [1,2,3]、[1,3,2]、[2,1,3]、[2,3,1]、[3,1,2]、[3,2,1] 共 6 种排列。

（二）核心挑战

1. 穷举所有排列：需要确保不重复、不遗漏地生成所有可能的排列。
2. 回溯的正确应用：在递归过程中，需要合理“选择”元素加入排列，递归返回后“撤销选择”（回溯 ），以尝试其他排列组合。
3. 状态标记：需要标记元素是否已被使用，避免重复选择同一元素。

二、算法思想：回溯算法的深度遍历

（一）回溯算法的核心

回溯算法是一种**深度优先搜索（DFS）**的变体，其核心思想是：

• 选择：在当前步骤，选择一个未使用的元素，加入当前排列。
• 递归：递归处理下一个位置，继续选择元素。
• 回溯：递归返回后，撤销当前选择（移除已加入的元素，标记为未使用 ），尝试其他选择。

这种“选 -> 递归 -> 回溯”的流程，能高效枚举所有排列组合，确保不重复、不遗漏。

（二）本题的回溯逻辑

1. 状态标记：使用布尔数组 used 标记元素是否已被加入当前排列，避免重复选择。
2. 递归终止条件：当当前排列的长度等于数组长度时，说明已生成一个完整排列，将其加入结果列表。
3. 选择与回溯：遍历数组中的每个元素，若未被使用，则加入当前排列，标记为已使用，递归处理下一个位置；递归返回后，移除该元素，标记为未使用，继续遍历下一个元素。

三、代码实现与详细解析

class Solution {// 存储所有全排列结果List<List<Integer>> result = new ArrayList<>(); // 存储当前正在构建的排列List<Integer> answer = new ArrayList<>(); // 标记元素是否已被使用boolean[] used; public List<List<Integer>> permute(int[] nums) {// 初始化 used 数组，长度与 nums 一致，默认值为 falseused = new boolean[nums.length]; // 启动回溯过程backtracking(nums); return result;}// 回溯方法：构建全排列public void backtracking(int[] nums) {// 终止条件：当前排列长度等于数组长度，说明已生成一个完整排列if (answer.size() == nums.length) { // 将当前排列加入结果（注意：需新建 ArrayList 避免引用问题）result.add(new ArrayList<>(answer)); return;}// 遍历数组中的每个元素for (int i = 0; i < nums.length; i++) { // 跳过已使用的元素if (used[i]) { continue;}// 选择：将未使用的元素加入当前排列answer.add(nums[i]); // 标记为已使用used[i] = true; // 递归：处理下一个位置，继续构建排列backtracking(nums); // 回溯：移除最后加入的元素answer.remove(answer.size() - 1); // 标记为未使用，供后续选择used[i] = false; }}
}

（一）代码流程拆解

1. 初始化：
   • result 存储所有全排列结果；answer 存储当前正在构建的排列；used 数组标记元素是否已被使用。
2. 启动回溯：调用 backtracking 方法，开始构建全排列。
3. 回溯逻辑：
   • 终止条件：当 answer 的长度等于 nums 的长度时，说明已生成一个完整排列，将其加入 result（需新建 ArrayList ，避免后续修改影响已存储的结果 ）。
   • 选择与递归：遍历数组，跳过已使用的元素；将未使用的元素加入 answer，标记为已使用；递归调用 backtracking ，处理下一个位置。
   • 回溯：递归返回后，移除 answer 中最后加入的元素，标记为未使用，继续尝试其他元素。
4. 返回结果：result 存储所有全排列，作为方法返回值。

（二）关键逻辑解析

• 状态标记的作用：used 数组确保每个元素在一个排列中只使用一次，避免重复选择，保证排列的唯一性。
• 回溯的本质：通过“选择 -> 递归 -> 回溯”的流程，枚举所有可能的排列组合。例如，生成 [1,2,3] 后，回溯移除 3 和 2，尝试 [1,3,2] ，以此类推。
• 引用问题处理：result.add(new ArrayList<>(answer)) 中，新建 ArrayList 存储当前 answer 的内容，避免后续 answer 的修改影响已存入的结果。

四、复杂度分析

（一）时间复杂度

• 全排列的总数为 n!（n 是数组长度 ），每个排列的生成需要 O(n) 的时间（构建列表、递归等 ）。
• 总体时间复杂度为 O(n × n!) ，主要受全排列数量和每个排列的处理时间影响。

（二）空间复杂度

• 递归栈的深度最多为 n（生成一个排列需要递归 n 次 ），空间复杂度为 O(n) 。
• result 存储所有排列，空间复杂度为 O(n × n!) ；answer 和 used 数组的空间复杂度为 O(n) 。
• 总体空间复杂度为 O(n × n!) ，主要受结果存储的影响。