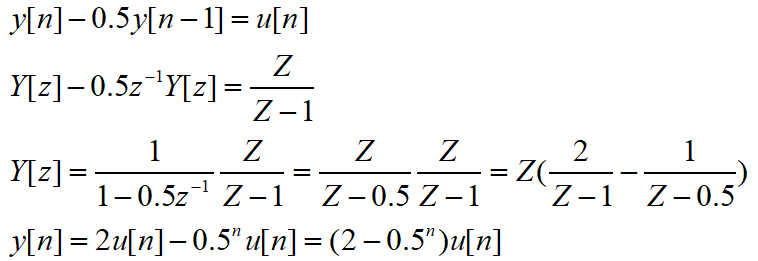1.6 傅里叶变换7-拉氏变换、Z变换

一、拉氏变换

1.1 拉氏变换的来源1

        某些x(t)因为发散，无傅里叶变换，但是乘以一个衰减更快的指数函数后就有了傅里叶变换。即下图

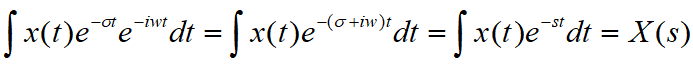
所以定义拉氏变换：

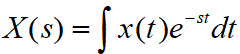
1.2 拉氏变换来源理解2

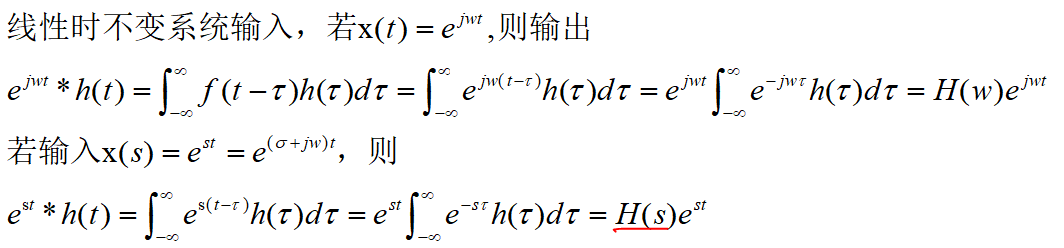
【备注]x(t)傅里叶变换和拉氏变换关系如下：

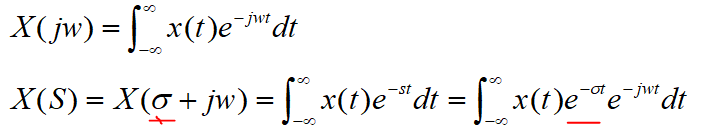
1.3 几个函数的拉氏变换

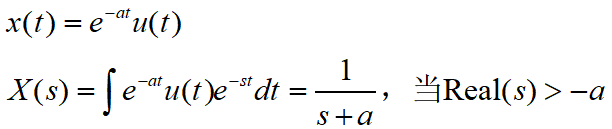
1.4拉氏变换的几个性质

1.5 拉氏变换用途之一-求解微分方程。

以RC电路，电容上电压为变量，加上恒定电压Vs,方程求解如下：

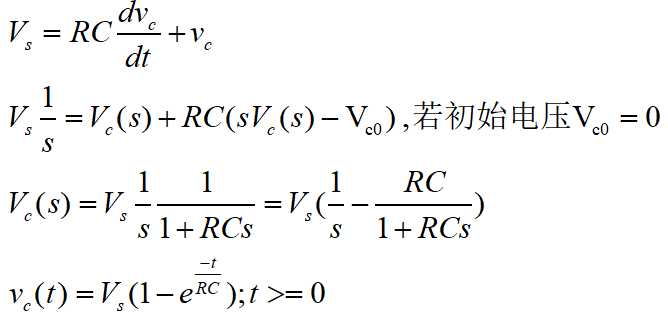
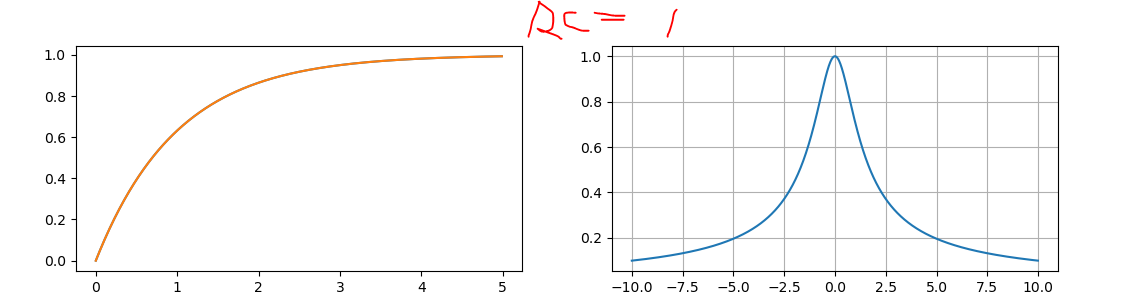
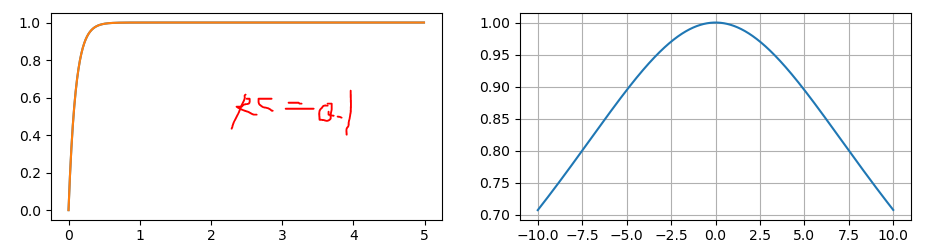
RC=1与RC=0.1时，其vc的曲线以及傅里叶变换下传递函数的幅值(1/（1+jRCw))：

可见对于电容上的电压，RC电路就是一个低通滤波器。RC越大，截止频率越低。

二、Z变换

2.1 Z变换的由来

a).x[n]的Z变换的表示与由来（角度1，为了使x[n]收敛）

b).线性时不变系统脉冲响应h[n]对复数序列响应（角度2，

【总之】Z变换的定义以及逆变换如下：

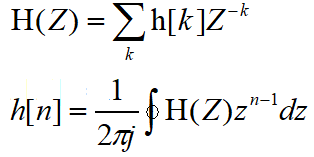
2.2 Z变换的性质

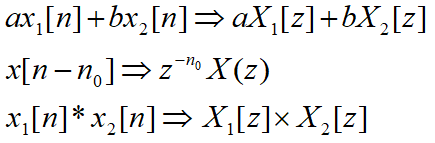
2.3 一些常用函数的Z变换

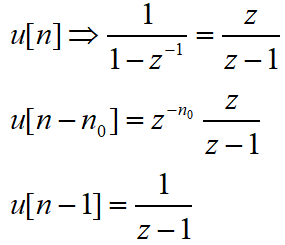
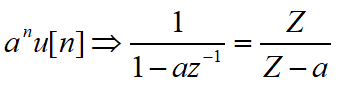
2.4 Z变换的一种作用示例：

Z变换的核心作用就在这里：它将离散时间的差分方程，转化为复数域（Z域）的代数方程，从而简化求解过程。