Multi-Target Position and Velocity Estimation Using OFDM Communication Signals

摘要—在本文中，我们考虑一个无源雷达系统，该系统利用一个完全非协作和非同步的照射源以及多个接收机发射的 OFDM 信号来估计多个运动目标的位置和速度。我们假设数据解调是基于直达路径信号独立进行的，并且易于出错的估计数据符号可用于无源雷达接收机，这些接收机分两个阶段来估计目标的位置和速度。首先，我们利用系统的两种稀疏性，即反射体 (即目标和杂波) 的数量和解调误差的数量都很小，构建了一个联合估计反射体的延迟多普勒和解调误差的问题。这个问题是非凸的，我们提出了一种共轭梯度下降法来求解。然后在第二阶段，我们根据第一阶段估计的延迟多普勒来确定目标的位置和速度。对于第二阶段，我们提出了两种方法：第一种是基于数值求解一组非线性方程，而第二种是基于神经网络，效率更高。我们通过大量的仿真来评估所提算法的性能。

索引术语—定位，速度估计，OFDM，无源雷达，超分辨率，非凸，共轭梯度下降，原子范数，神经网络，离网格，稀疏性。

旨在估计目标的位置和速度。第一阶段旨在通过利用两种稀疏性来估计延迟多普勒频移和解调误差：

• 一方面，由于目标和杂波在空间中是稀疏分布的，因此到达雷达接收机的反射信号是稀疏的，即反射信号的数量远小于信号的长度；
• 另一方面，通信系统的解调错误率在正常工作条件下通常很低，因此解调误差信号也是稀疏的，即解调误差信号中的非零项数量 (根据 ($14$) 中 $\mathbf{e}$ 的非零项数量) 远小于解调误差信号的长度 (根据 ($14$) 中的 $N_b{N}_d$)。

由于目标的延迟和多普勒频移是连续参数，当信号不能被有限离散字典 [27]–[29] 稀疏表示时，传统的压缩感知 (CS) 工具 [25] 可能会导致性能不佳 [26]。我们利用最近发展的用于超分辨率的连续稀疏恢复数学理论 [30]–[32]，特别是原子范数 (atomic norm，AN) 最小化技术，该技术已成功应用于连续频率恢复、线谱估计和到达方向估计 [32]–[35]。请注意，与 [3] 中针对单个接收机的延迟多普勒估计的凸问题不同，在我们的模型中，不同的接收机共享相同的估计数据符号并施加相同的约束，这由于决策变量乘积项的存在而产生了一个非凸问题。因此，我们使用非凸分解 (non-convex factorization，NF) 将问题转化为一个光滑的无约束优化问题，然后通过共轭梯度下降 (conjugate gradient descent，CGD) 算法来求解。

第二阶段旨在根据第一阶段的估计值来确定目标的位置和速度。由于照射源和接收机是不同步（un-synchronizated）的，我们利用不同接收机之间的延迟差来计算每个目标的位置。

• 第一种方法是数值求解一组非线性方程，
• 第二种方法是利用神经网络 [36]–[38] 来估计目标位置，这种方法计算效率更高。然后可以根据估计的目标位置和多普勒频移来确定相应的目标速度。

我们提供了大量的仿真结果，以说明所提出的方法能够准确地估计目标的位置和速度。

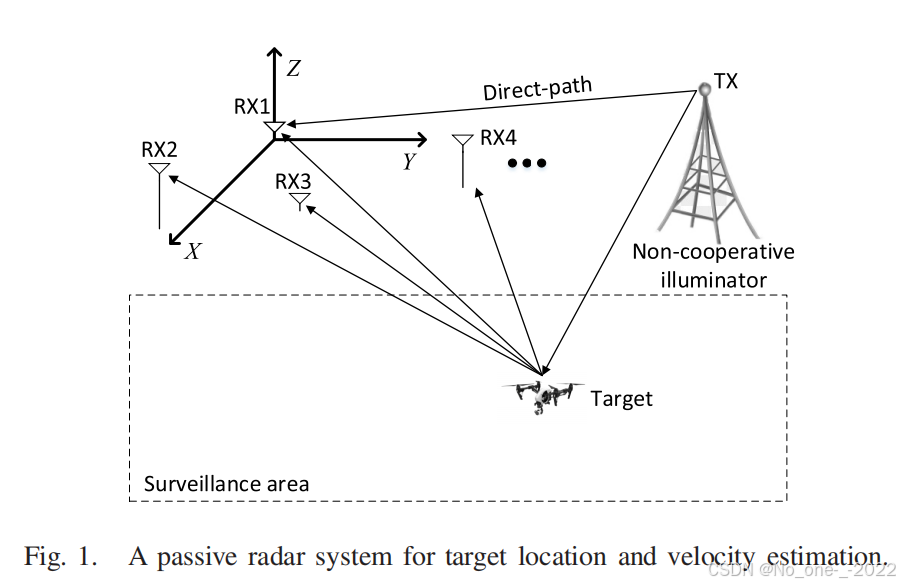
II. SYSTEM DESCRIPTIONS & PROBLEM FORMULATION

A. System Descriptions

如图 1 所示，我们考虑一个由 $M$ ($M\ge 4$) 个接收机和一个非协作照射源组成的无源雷达系统，用于估计三维笛卡尔坐标系中多个目标的位置和速度。假设照射源和接收机 $m$ 的坐标分别为 ${\mathbf{p}}_0=[p_0^x,p_0^y,p_0^z{]}^T$ 和 ${\mathbf{p}}_m=[p_m^x,p_m^y,p_m^z{]}^T$，其中 $m=1,\dots ,M$。假设监控区域内有 $L$ 个反射体，包括目标和杂波。注意，我们将杂波视作零速目标。设 ${\mathbf{x}}_{\ell }=[x_{\ell }^x,x_{\ell }^y,x_{\ell }^z{]}^T$ 和 ${\mathbf{v}}_{\ell }=[v_{\ell }^x,v_{\ell }^y,v_{\ell }^z{]}^T$ 分别为第 $\ell$ 个反射体的位置和速度。那么，从照射源到第 $m$ 个接收天线，由第 $\ell$ 个反射体引起的传播时间为

$${\bar{\tau }}_{\ell ,m}=\frac{1}{c}(\Vert {\mathbf{p}}_0-{\mathbf{x}}_{\ell }{\Vert }_2+\Vert {\mathbf{p}}_m-{\mathbf{x}}_{\ell }{\Vert }_2),\text{\hspace{1em}(1)}$$

其中 $c$ 是光在自由空间中的速度；$\Vert \cdot {\Vert }_2$ 表示 $l_2$ 范数。相应的多普勒频移由 [39] 给出

$$f_{\ell ,m}=\frac{{\mathbf{v}}_{\ell }^T({\mathbf{p}}_0-{\mathbf{x}}_{\ell })}{\lambda \Vert {\mathbf{p}}_0-{\mathbf{x}}_{\ell }{\Vert }_2}+\frac{{\mathbf{v}}_{\ell }^T({\mathbf{p}}_m-{\mathbf{x}}_{\ell })}{\lambda \Vert {\mathbf{p}}_m-{\mathbf{x}}_{\ell }{\Vert }_2},\text{\hspace{1em}(2)}$$

其中 $\lambda$ 表示载波的波长。假设 $s(t)$ 是未知的通信信号。由于目标和杂波的反射，在第 $m$ 个接收机接收到的信号为

$$y_m(t)=s_m^d(t)+\sum _{\ell =1}^L{c}_{\ell ,m}{e}^{i2\pi f_{\ell ,m}t}s(t-{\bar{\tau }}_{\ell ,m}+{\Delta }_{\tau })+w_m(t),\text{\hspace{1em}(3)}$$

其中 $c_{\ell ,m}$ 是第 $m$ 个接收天线上第 $\ell$ 条路径的复增益¹；$s_m^d(t)={\tilde{c}}_{m}s(t-{\tilde{\tau }}_m)$ 是直达路径 (照射源到接收机) 信号，其中 ${\tilde{c}}_m$ 和 ${\tilde{\tau }}_m$ 分别是到第 $m$ 个接收天线的直达路径的复增益和传播时间²；$w_m(t)$ 是一个复圆对称高斯白噪声过程；${\Delta }_{\tau }$ 是发射机和接收机之间的同步误差，即我们假设雷达接收机共享相同的时钟，但与通信发射机不同步。

¹ 在本文中，我们假设复增益不随频率变化，例如，0 型和 1 型斯威林 (Swerling) 反射器 [2]。

² 注意直达路径信号 $s_m^d(t)$ 可以通过 [15] 中的空间滤波方法或使用参考信道来手机发射机信号 [1], [2], [40]，即，使用窄波束天线对准发射机以接收直达路径信号 [40]，或使用接收天线的旁瓣来接收直达路径信号 [2]。

B. OFDM-Based Passive Radar Signal Model

在本文中，我们假设信号 $s(t)$ 是在现代无线通信系统中被广泛采用的 OFDM 信号。OFDM 信号由 $N_d$ 个数据子载波和 $NT=(N_d+N_p)T$ 个基本时间单位组成，其中 $N_p$ 是循环前缀 (CP) 载波的数量，$T$ 是采样周期 (“子脉冲持续时间”)。那么，发射的基带 OFDM 信号由下式给出

$$s(t)=\sum _{n=0}^{N_b-1}\sum _{k=0}^{N_d-1}{b}_n(k)e^{i2\pi \frac{k}{N_{d}T}t}u(t-nNT),\text{\hspace{1em}(4)}$$

其中 $b_n(k)$，$k=0,\dots ,N_d-1$ 是第 $n$ 个归一化数据符号块，使得 $\mathbb{E}[b_n(k)b_n(k{)}^{\ast }]=1$，$(\cdot {)}^{\ast }$ 表示复共轭算子；u(t)={1,t∈[−NpT,NdT],0,otherwise}u(t) = \{1, t \in [-N_pT, N_dT], 0, \text{otherwise}\}u(t)={1,t∈[−Np​T,Nd​T],0,otherwise}。

在每个雷达接收机 $m$ 处，假设直达路径信号 $y_m^d(t)$ 首先被移除，我们只处理经过下变频的基带信号。CP 被移除，假设其长度不小于最大路径延迟，即 NpT>max⁡m,ℓ{τˉℓ,m−Δτ}N_pT > \max_{m,\ell} \{\bar{\tau}_{\ell,m} - \Delta_\tau\}Np​T>maxm,ℓ​{τˉℓ,m​−Δτ​}。注意数据符号 $b_n(k)$ 是未知的，但可以通过使用直达路径信号 $s_m^d(t)$ [1] 进行解调来估计³。因此在下文中，我们假设数据符号的估计值 ${\hat{b}}_n(k)$ 是可用的，使得

$$b_n(k)={\hat{b}}_n(k)+e_n(k),k=0,\dots ,N_d-1,\text{\hspace{1em}(5)}$$

³ 我们假设直达路径信号 $s_m^d(t)$ 的接收信噪比足够高，可以成功进行解调。

其中 $e_n(k)$ 表示相应的解调误差。此外，我们假设目标的速度很低。使得 ${\bar{f}}_{\ell ,m}NT\ll 1$。因此，由多普勒频移引起的相位旋转在一个 OFDM 符号周期 $NT$ 内可以近似为常数，即 [3], [22]

$$e^{i2\pi {\bar{f}}_{\ell ,m}t}\approx e^{i2\pi {\bar{f}}_{\ell ,m}nNT},t\in [nNT,(n+1)NT].\text{\hspace{1em}(6)}$$

在每个接收机 $m$ 处，对第 $n$ 个 OFDM 符号进行匹配滤波，以获得 (对于 $k=0,\dots ,N_d-1$)

$$\begin{array}{rl}{\tilde{y}}_{n,m}(k)& =\frac{1}{N_{d}T}{\int }_{nNT}^{nNT+N_{d}T}(y_m(t)-s_m^d(t))e^{-i2\pi \frac{k}{N_{d}T}t}dt+{\tilde{w}}_{n,m}(k)\\ & =\sum _{\ell =1}^L{c}_{\ell ,m}\sum _{q=0}^{N_d-1}{b}_n(q)\frac{1}{N_{d}T}{\int }_{nNT}^{nNT+N_{d}T}\\ & \times e^{i2\pi {\bar{f}}_{\ell ,m}t}{e}^{i2\pi q\frac{t-{\bar{\tau }}_{\ell ,m}+{\Delta }_{\tau }}{N_{d}T}}{e}^{-i2\pi \frac{k}{N_{d}T}t}dt+{\tilde{w}}_{n,m}(k)\\ & \approx e^{i2\pi {\bar{f}}_{\ell ,m}nNT}\sum _{\ell =1}^L{c}_{\ell ,m}{e}^{i2\pi {\bar{f}}_{\ell ,m}nNT}\sum _{q=0}^{N_d-1}{b}_n(q)e^{-i2\pi q\frac{{\bar{\tau }}_{\ell ,m}-{\Delta }_{\tau }}{N_{d}T}}\\ & \times \underset{N_{d}T\cdot \delta (q-k)}{\underbrace{\frac{1}{N_{d}T}{\int }_{nNT}^{nNT+N_{d}T}{e}^{i2\pi (q-k)\frac{t}{N_{d}T}}dt}}+{\tilde{w}}_{n,m}(k)\\ & =({\hat{b}}_n(k)+e_n(k))\sum _{\ell =1}^L{c}_{\ell ,m}{e}^{i2\pi n{f}_{\ell ,m}}{e}^{-i2\pi k{\tau }_{\ell ,m}}+{\tilde{w}}_{n,m}(k),\end{array}\text{\hspace{1em}(7)(8)}$$

其中 ${\tilde{w}}_{n,m}(k)=\frac{1}{N_{d}T}{\int }_{nNT}^{nNT+N_{d}T}{w}_m(t)e^{-i2\pi \frac{k}{N_{d}T}t}dt$ 并且

$${\tau }_{\ell ,m}=\frac{{\bar{\tau }}_{\ell ,m}-{\Delta }_{\tau }}{N_{d}T}\in [0,1),f_{\ell ,m}={\bar{f}}_{\ell ,m}NT\in [0,1).\text{\hspace{1em}(9)}$$

C. Problem Formulation

现在我们定义 ${\mathbf{c}}_m=[c_{1,m},c_{2,m},\dots ,c_{L,m}{]}^T\in {\mathbb{C}}^{L\times 1}$，${\mathbf{f}}_m=[f_{1,m},f_{2,m},\dots ,f_{L,m}{]}^T\in {\mathbb{C}}^{L\times 1}$，${\tau }_m=[{\tau }_{1,m},{\tau }_{2,m},\dots ,{\tau }_{L,m}{]}^T\in {\mathbb{C}}^{L\times 1}$，以及导向矢量 $\mathbf{s}(f)=[1,e^{i2\pi f},\dots ,e^{i2\pi (N_b-1)f}{]}^T\in {\mathbb{C}}^{N_b\times 1}$ 和 $\mathbf{d}(\tau )=[1,e^{i2\pi \tau },\dots ,e^{i2\pi (N_d-1)\tau }{]}^T\in {\mathbb{C}}^{N_d\times 1}$。相应地，响应矩阵定义为 $\mathbf{S}({\mathbf{f}}_m)=[\mathbf{s}(f_{1,m}),\mathbf{s}(f_{2,m}),\dots ,\mathbf{s}(f_{L,m})]\in {\mathbb{C}}^{N_b\times L}$ 和 $\mathbf{D}({\tau }_m)=[\mathbf{d}({\tau }_{1,m}),\mathbf{d}({\tau }_{2,m}),\dots ,\mathbf{d}({\tau }_{L,m})]\in {\mathbb{C}}^{N_d\times L}$。那么 (8) 可以写成如下的矩阵形式

$${\bar{\mathbf{Y}}}_m=(\hat{\mathbf{B}}+\mathbf{E})\odot (\mathbf{S}({\mathbf{f}}_m)\text{diag}({\mathbf{c}}_m)\mathbf{D}({\tau }_m{)}^H)+{\bar{\mathbf{W}}}_m,\text{\hspace{1em}(10)}$$

其中 $\odot$ 表示哈达玛积 (Hadamard product)；$\text{diag}({\mathbf{c}}_m)$ 表示对角元素为 ${\mathbf{c}}_m$ 的对角矩阵；${\bar{\mathbf{Y}}}_m\in {\mathbb{C}}^{N_b\times N_d}$, $\hat{\mathbf{B}}\in {\mathbb{C}}^{N_b\times N_d}$, $\mathbf{E}\in {\mathbb{C}}^{N_b\times N_d}$ 和 ${\bar{\mathbf{W}}}_m\in {\mathbb{C}}^{N_b\times N_d}$ 是矩阵，其 $(n,k)$ 位置的元素分别为 ${\tilde{y}}_{n,m}(k)$, ${\hat{b}}_n(k)$, $e_n(k)$ 和 ${\tilde{w}}_{n,m}(k)$。进一步表示 $\bar{\mathbf{b}}=\text{vec}(\hat{\mathbf{B}})\in {\mathbb{C}}^{N_b{N}_d\times 1}$, $\bar{\mathbf{e}}=\text{vec}(\mathbf{E})\in {\mathbb{C}}^{N_b{N}_d\times 1}$, ${\bar{\mathbf{w}}}_m=\text{vec}({\bar{\mathbf{W}}}_m)\in {\mathbb{C}}^{N_b{N}_d\times 1}$，其中 $\text{vec}(\cdot )$ 是向量化算子，以及

$${\varphi }_m=\sum _{\ell =1}^L{c}_{\ell ,m}\mathbf{a}({\tau }_{\ell ,m},f_{\ell ,m})\in {\mathbb{C}}^{N_b{N}_d\times 1},\text{\hspace{1em}(11)}$$

其中

$$\mathbf{a}(\tau ,f)=\mathbf{d}(\tau {)}^{\ast }\otimes \mathbf{s}(f)\in {\mathbb{C}}^{N_b{N}_d\times 1},\text{\hspace{1em}(12)}$$

以及 $\otimes$ 是克罗内克积 (Kronecker product)。然后我们将 (10) 中的 ${\bar{\mathbf{Y}}}_m$ 向量化以获得

$$\begin{array}{rl}{\bar{\mathbf{y}}}_m& =\text{vec}({\bar{\mathbf{Y}}}_m)=\text{diag}(\hat{\mathbf{b}}+\bar{\mathbf{e}})(\mathbf{D}({\tau }_m{)}^{\ast }\circ \mathbf{S}({\mathbf{f}}_m)){\mathbf{c}}_m+{\bar{\mathbf{w}}}_m\\ & =\text{diag}(\hat{\mathbf{b}}+\bar{\mathbf{e}}){\varphi }_m+{\bar{\mathbf{w}}}_m,\end{array}\text{\hspace{1em}(13)}$$

$$\mathrm{vec}(\mathbf{A}\odot \mathbf{B})=\mathrm{diag}(\mathrm{vec}(\mathbf{A}))\mathrm{vec}(\mathbf{B})$$

其中 $\circ$ 是哈特里-拉奥积 (Khatri-Rao product)；$(\mathbf{D}({\tau }_m{)}^{\ast }\circ \mathbf{S}({\mathbf{f}}_m))\in {\mathbb{C}}^{N_b{N}_d\times L}$ 是一个矩阵，其第 $\ell$ 列的形式为 ${\mathbf{d}}^{\ast }({\tau }_{\ell ,m})\otimes \mathbf{s}(f_{\ell ,m})$。最后，(13) 可以重写为如下矩阵形式

$$\mathbf{Y}=\text{diag}(\hat{\mathbf{b}}+\bar{\mathbf{e}})\mathbf{\Phi }+\mathbf{W},\text{\hspace{1em}(14)}$$

其中 $\mathbf{Y}\in {\mathbb{C}}^{N_b{N}_d\times M}$, $\mathbf{\Phi }\in {\mathbb{C}}^{N_b{N}_d\times M}$ 和 $\mathbf{W}\in {\mathbb{C}}^{N_b{N}_d\times M}$ 的第 $m$ 列分别是 ${\bar{\mathbf{y}}}_m$, ${\varphi }_m$ 和 ${\bar{\mathbf{w}}}_m$。

在本文中，我们首先从接收信号 $\mathbf{Y}$ 中估计包含在 $\mathbf{\Phi }$ 中的延迟和多普勒频移 {τℓ,m,fℓ,m}\{\tau_{\ell,m}, f_{\ell,m}\}{τℓ,m​,fℓ,m​}。然后基于这些估计，我们进一步估计反射体的位置和速度 {xℓ,vℓ}\{\mathbf{x}_\ell, \mathbf{v}_\ell\}{xℓ​,vℓ​}，其中 ${\mathbf{v}}_{\ell }\approx 0$ 的那些被认为是杂波。

III. STAGE 1: DELAY-DOPPLER ESTIMATION

在本节中，我们提出一种 CGD 方法来估计 (14) 中的延迟和多普勒频移 {τℓ,m,fℓ,m}\{\tau_{\ell,m}, f_{\ell,m}\}{τℓ,m​,fℓ,m​}。我们首先利用两种类型的稀疏性来构建一个非凸优化问题。然后，我们将这个非凸优化问题松弛为一个光滑的无约束形式。这个光滑化的问题随后可以通过 CGD 来求解。

A. Non-Convex Optimization Problem Setup

我们将利用以下两种稀疏性：首先，反射体的数量 $L\ll N_b{N}_d$ (在 (11) 中)；其次，假设解调错误率很低，误差向量 $\mathbf{e}$ 只有少量非零项，即 $\Vert \mathbf{e}{\Vert }_0\ll N_b{N}_d$，其中 $\Vert \cdot {\Vert }_0$ 是 ${\ell }_0$ 范数。由于延迟 $\tau$ 和多普勒频移 $f$ 取连续值，我们使用原子范数 [42] 来利用第一种稀疏性。令 A={a(τ,f):τ∈[0,1),f∈[0,1)}\mathcal{A} = \{\mathbf{a}(\tau,f) : \tau \in [0,1), f \in [0,1)\}A={a(τ,f):τ∈[0,1),f∈[0,1)} 为原子集，其中 $\mathbf{a}(\tau ,f)$ 在 (12) 中定义。那么，对于 $m=1,\dots ,M$，${\varphi }_m$ 的二维原子范数 [32] 定义为

∥ϕm∥A=inf⁡{χ>0:ϕm∈χconv(A)}=inf⁡cℓ,m∈C,τℓ,m∈[0,1),fℓ,m∈[0,1){∑ℓ∣cℓ,m∣:ϕm=∑ℓcℓ,ma(τℓ,m,fℓ,m)},(15) \|\mathbf{\phi}_m\|_{\mathcal{A}} = \inf \left\{ \chi > 0: \mathbf{\phi}_m \in \chi \text{conv}(\mathcal{A}) \right\} = \inf_{c_{\ell,m} \in \mathbb{C}, \tau_{\ell,m} \in [0,1), f_{\ell,m} \in [0,1)} \left\{ \sum_\ell |c_{\ell,m}| : \mathbf{\phi}_m = \sum_{\ell} c_{\ell,m} \mathbf{a}(\tau_{\ell,m}, f_{\ell,m}) \right\}, \tag{15} ∥ϕm​∥A​=inf{χ>0:ϕm​∈χconv(A)}=cℓ,m​∈C,τℓ,m​∈[0,1),fℓ,m​∈[0,1)inf​{ℓ∑​∣cℓ,m​∣:ϕm​=ℓ∑​cℓ,m​a(τℓ,m​,fℓ,m​)},(15)

其中 $\text{conv}(\cdot )$ 表示输入集的凸包。原子范数可以在原子集 $\mathcal{A}$ 中强制稀疏性。注意矩阵 $\mathbf{\Phi }$ 中的列是独立的，并且有其自身的稀疏性。在此基础上，我们的延迟-多普勒估计问题可以根据 (14) 构建为：

$$(\hat{\mathbf{\Phi }},\hat{\mathbf{e}})=\arg \underset{\begin{array}{c}\mathbf{\Phi }\in {\mathbb{C}}^{N_b{N}_d\times M}\\ \mathbf{e}\in {\mathbb{C}}^{N_b{N}_d\times 1}\end{array}}{\min }\frac{1}{2}\Vert \mathbf{Y}-\text{diag}(\hat{\mathbf{b}}+\mathbf{e})\mathbf{\Phi }{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\varphi }_m{\Vert }_{\mathcal{A}}+\eta \Vert \mathbf{e}{\Vert }_1,\text{\hspace{1em}(16)}$$

其中 $\Vert \cdot {\Vert }_1$ 表示 ${\ell }_1$ 范数，$\gamma >0$ 和 $\eta >0$ 是权重因子。

然而，通过原子范数寻找谐波分量是一个在所有可行的 $\tau$ 和 $f$ 上的无限规划问题。为便于计算，我们使用 (15) 对于 $m=1,\dots ,M$ 的等价形式 [32], [43]

$$\Vert {\varphi }_m{\Vert }_{\mathcal{A}}=\underset{\begin{array}{c}{\mathbf{Q}}_m\in {\mathbb{C}}^{(2N_b-1)\times (2N_d-1)}\\ {\nu }_m\in \mathbb{R}\end{array}}{\min }\left\{\frac{1}{2N_b{N}_d}\text{Tr}(\mathbb{T}({\mathbf{Q}}_m))+\frac{{\nu }_m}{2}\right\},\text{s.t.}\left[\begin{array}{cc}\mathbb{T}({\mathbf{Q}}_m)& {\varphi }_m\\ {\varphi }_m^H& {\nu }_m\end{array}\right]⪰0,\text{\hspace{1em}(17)}$$

其中 $\text{Tr}(\cdot )$ 表示迹算子，$⪰0$ 代表一个半正定矩阵，$\mathbb{T}(\cdot )$ 接收一个 $(2N_b-1)\times (2N_d-1)$ 的矩阵作为输入

$${\mathbf{Q}}_m=[{\mathbf{q}}_{m,-N_d+1},{\mathbf{q}}_{m,-N_d+2},\dots ,{\mathbf{q}}_{m,N_d-1}]\in {\mathbb{C}}^{(2N_b-1)\times (2N_d-1)},\text{\hspace{1em}(18)}$$

其中

$${\mathbf{q}}_{m,n}=[q_{m,n}(-N_b+1),q_{m,n}(-N_b+2),\dots ,q_{m,n}(N_b-1){]}^T\in {\mathbb{C}}^{(2N_b-1)\times 1},\text{\hspace{1em}(19)}$$

$n=-N_d+1,-N_d+2,\dots ,N_d-1$，并输出一个 $N_b{N}_d\times N_b{N}_d$ 的块托普利茨 (block Toeplitz) 矩阵

$$\mathbb{T}({\mathbf{Q}}_m)=\left[\begin{array}{cccc}\text{Toep}({\mathbf{q}}_{m,0})& \text{Toep}({\mathbf{q}}_{m,-1})& \cdots & \text{Toep}({\mathbf{q}}_{m,-N_d+1})\\ \text{Toep}({\mathbf{q}}_{m,1})& \text{Toep}({\mathbf{q}}_{m,0})& \cdots & \text{Toep}({\mathbf{q}}_{m,-N_d+2})\\ ⋮& ⋮& \ddots & ⋮\\ \text{Toep}({\mathbf{q}}_{m,N_d-1})& \text{Toep}({\mathbf{q}}_{m,N_d-2})& \cdots & \text{Toep}({\mathbf{q}}_{m,0})\end{array}\right]\in {\mathbb{C}}^{N_b{N}_d\times N_b{N}_d}\text{\hspace{1em}(20)}$$

其中 $\text{Toep}(\cdot )$ 输出一个以 (19) 中的 ${\mathbf{q}}_{m,n}\in {\mathbb{C}}^{(2N_b-1)\times 1}$ 为输入的 $N_b\times N_b$ 托普利茨矩阵。更具体地说，我们有

$$\text{Toep}({\mathbf{q}}_{m,n})=\left[\begin{array}{cccc}{q}_{m,n}(0)& q_{m,n}(-1)& \cdots & q_{m,n}(-N_b+1)\\ q_{m,n}(1)& q_{m,n}(0)& \cdots & q_{m,n}(-N_b+2)\\ ⋮& ⋮& \ddots & ⋮\\ q_{m,n}(N_b-1)& q_{m,n}(N_b-2)& \cdots & q_{m,n}(0)\end{array}\right]\in {\mathbb{C}}^{N_b\times N_b},\text{\hspace{1em}(21)}$$

$n=-N_d+1,-N_d+2,\dots ,N_d-1$。

当达到最优解时，公式 (15) 和 (17) 通过以下关系相关联

$$\mathbb{T}({\mathbf{Q}}_m)=\sum _{\ell ,m}|c_{\ell ,m}|\mathbf{a}({\tau }_{\ell ,m},f_{\ell ,m})\mathbf{a}({\tau }_{\ell ,m},f_{\ell ,m}{)}^H,\text{\hspace{1em}(22)}$$

$${\nu }_m=\sum _{\ell ,m}|c_{\ell ,m}|.\text{\hspace{1em}(23)}$$