当前位置：首页 > news >正文

【微科普】PCA 与非线性降维的人文思考

news 2025/10/4 13:01:19

🌿 序章：书桌前的维度减法 ——PCA 与非线性降维的人文思考

周末整理书桌时，总被散落的笔记本、充电线和书籍淹没。明明只需要常用的几样物品，却要在一堆冗余中翻找 —— 这像极了高维数据的困境：消费记录里的 10 个指标、图像里的百万像素、基因测序的数千位点，信息藏在维度的 “杂物堆” 里，既难分析又难可视化。

“技术是数据的收纳盒，不是简单删减，而是在维度减法里保留最核心的脉络。” 从 PCA（主成分分析）的线性整理，到核 PCA 的非线性 “解缠绕”，再到 t-SNE 的可视化 “归队”，降维算法始终在做一件事：让复杂数据像整理好的书桌一样，清晰、有序，且核心信息丝毫无损。

📦 第一章：发现问题 —— 高维数据的 “杂乱困境”

生活里的 “高维痛点” 随处可见：

网购平台给用户贴了 20 个标签（消费力、购买频率、偏好品类等），想分析用户群体时，20 个维度根本无法画图，只能对着表格 “盲人摸象”；
手机拍一张 1000x1000 像素的照片，本质是 100 万个维度的数组，直接用这些数据做图像识别，电脑会因 “数据过载” 变慢；
实验室测了 50 种土壤指标（pH 值、湿度、养分含量等），但很多指标高度相关（比如湿度高时养分流失快），重复信息反而干扰结论。

这些问题的核心是维度冗余与信息重叠—— 就像书桌里 “笔” 和 “笔记本” 总是一起用，数据里 “消费额” 和 “购买频次” 也高度相关。此时需要一种技术：既能减少维度数量，又能留住大部分关键信息，这就是降维算法的使命。

🛠️ 第二章：技术思路 —— 从 “线性整理” 到 “非线性解缠”

降维的本质是 “找核心”，就像整理书桌时优先保留 “常用物品”（核心信息），收起 “偶尔用” 的物品（冗余信息）。但数据的 “形状” 不同，需要不同的 “整理工具”：

1. PCA：线性数据的 “分层收纳”

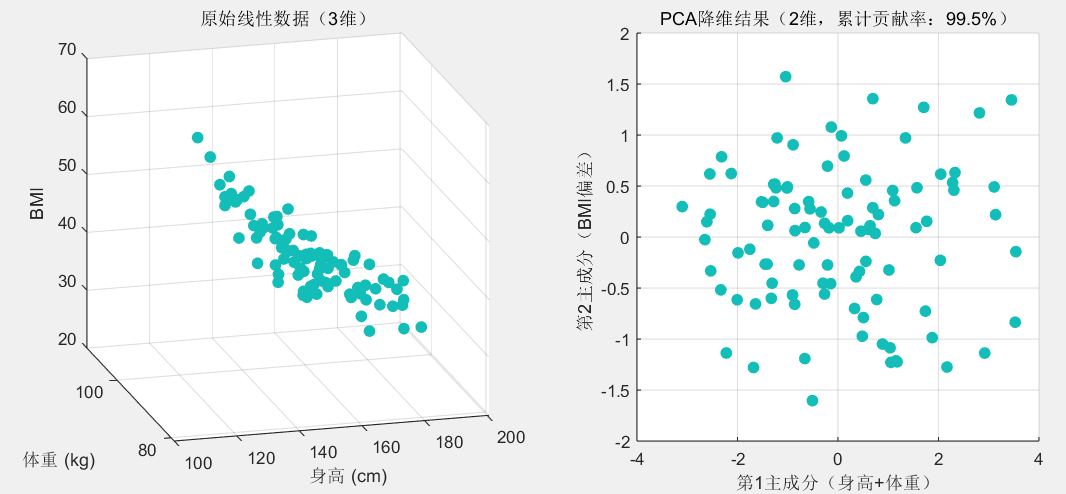
如果数据是 “整齐的堆叠”（线性相关），比如 “身高、体重、BMI” 三个维度（BMI 由身高体重计算而来，高度冗余），PCA 就像给书桌分层：

第一层（第一主成分）：放最常用的 “身高 + 体重” 组合，这一层能解释 80% 的信息（比如身高体重决定了人的体型核心特征）；
第二层（第二主成分）：放 “BMI 偏差”，解释 15% 的信息；
下层（剩余成分）：放无关紧要的噪声，只占 5% 信息。

取前两层就能保留 95% 的信息，维度从 3 减到 2，既简洁又不丢失核心。

2. 核 PCA：非线性数据的 “解缠绕”

如果数据是 “缠绕的耳机线”（非线性分布），比如螺旋状的二维数据（绕成一圈，线性降维会把相邻点拉远），PCA 就失效了 —— 就像用线性思维整理缠绕的耳机线，越理越乱。

核 PCA 的思路是 “换个空间解缠”：

先把螺旋数据 “掰直”—— 用核函数（比如 RBF 核）把数据映射到更高维空间（比如从 2 维升到 10 维），在高维空间里，螺旋变成了 “直线堆叠”；
再用 PCA 在高维空间做线性降维，最后投影回低维，就能得到解开缠绕的清晰数据。

这像把缠绕的耳机线放进三维盒子里，展开后再平铺到桌面，瞬间变整齐。

3. t-SNE：高维数据的 “可视化归队”

如果目标是 “看清数据分类”（比如识别手写数字，10 个数字对应 10 类数据），t-SNE 更擅长 —— 它像给书桌做 “分类收纳”：

把相似的数据（比如所有写着 “5” 的手写体）归为一队，在低维图上靠得近；
把不同的数据（比如 “5” 和 “8”）分开，避免拥挤（用 t 分布减少 “热门区域” 的拥挤问题，比如避免所有数字都挤在图中央）。

比如把 1000 维的手写数字数据，用 t-SNE 降到 2 维，就能在散点图上清晰看到 10 个颜色的 “小队伍”，每个队伍对应一个数字。

📐 第三章：数学之美 —— 从公式到生活逻辑

降维不是 “拍脑袋删维度”，而是有严谨的数学支撑。我们用 “生活类比” 拆解核心公式，避免复杂推导：

1. PCA 的核心：协方差矩阵与特征值

PCA 的关键是找到 “信息最多的方向”（主成分），靠的是协方差矩阵和特征值分解。

协方差矩阵：衡量 “维度间的相关性”，就像计算 “笔和笔记本的关联度”。公式：Cov(X,Y)=n−11∑i=1n(Xi−Xˉ)(Yi−Yˉ)类比：每周记录 “用笔次数” 和 “用笔记本次数”，计算两者的 “偏差乘积平均值”—— 如果笔用得多时笔记本也用得多，协方差为正，说明高度相关。协方差矩阵里的元素Cov(Xi,Xj)，就是所有维度两两之间的相关性，矩阵越 “非对角化”，说明维度冗余越严重。
特征值分解：给协方差矩阵 “排序”，就像给书桌物品 “按常用程度排队”。公式：C=QΛQT（C 是协方差矩阵，Q 是特征向量矩阵，Λ 是特征值对角阵）类比：Q 是 “排队顺序”（主成分方向），比如 “身高→体重→BMI”；Λ 是 “每个位置的空间大小”（特征值大小），空间越大，说明这个方向的信息越多。取前 k 个特征值对应的特征向量，就是保留了 “信息最多的 k 个方向”，维度从 d 减到 k。

2. 核 PCA 的核心：核函数的 “空间转换”

核 PCA 不用直接计算高维映射（避免 “维度灾难”），而是用核函数间接计算高维空间的内积。公式：K(xi,xj)=ϕ(xi)⋅ϕ(xj)（ϕ是高维映射，K 是核函数）类比：不用把耳机线真的放进三维盒子，而是通过 “触摸耳机线的缠绕规律”（核函数），间接知道它在三维空间的展开状态。常用的 RBF 核：K(xi,xj)=exp(−2σ2∣∣xi−xj∣∣2)，σ是 “触摸的灵敏度”——σ太小，会把相邻点当成无关点；σ太大，会把所有点当成相似点。

3. t-SNE 的核心：相似度的 “保持”

t-SNE 的目标是 “高维相似的点，低维也相似”，靠的是概率分布匹配。

高维空间：用高斯分布计算两点的相似度（比如两个 “5” 的手写体，相似度高，概率大）；
低维空间：用 t 分布计算两点的相似度（t 分布的 “长尾” 能避免拥挤，比如两个 “5” 即使离得稍远，也能被识别为同类）；
通过优化 “两个分布的差距”（KL 散度），让低维分布尽量贴近高维分布。类比：给班级同学排座位时，先统计 “谁和谁经常一起玩”（高维相似度），再按这个统计排座位（低维分布），确保好朋友坐近，同时避免某片区域太挤。

💻 第四章：实践落地 ——MATLAB 脚本实现与可视化

以下是完整的 MATLAB 脚本，包含 “PCA→核 PCA→t-SNE” 的实现，涵盖线性数据、非线性螺旋数据、手写数字简化数据的降维与可视化。脚本无需额外工具箱，注释详细，运行后可直观看到三种算法的效果差异。

脚本功能说明

生成三类测试数据：线性相关数据（模拟身高、体重、BMI）、螺旋非线性数据（模拟缠绕的高维数据）、MNIST 简化数据（模拟手写数字高维数据）；
实现 PCA 降维，可视化 “主成分选择” 与 “降维后效果”；
实现核 PCA（RBF 核）降维，对比不同σ值的效果；
调用 MATLAB 自带 t-SNE 函数，可视化手写数字的降维分类效果；
输出 “方差贡献率”“相似度匹配度” 等关键指标，解读结果意义。

% 降维算法实践：PCA + 核PCA + t-SNE（修正版）clear; clc; close all;%% 1. 数据生成模块
rng(1); 
n = 100; 
height = 160 + 20*randn(n,1);
weight = 50 + 0.3*height + 5*randn(n,1);
bmi = weight ./ ((height/100).^2);
linear_data = [height, weight, bmi];
linear_label = ones(n,1);theta = linspace(0, 4*pi, n);
spiral_x = theta.*cos(theta) + 0.5*randn(n,1);
spiral_y = theta.*sin(theta) + 0.5*randn(n,1);
nonlinear_data = [spiral_x, spiral_y];
nonlinear_label = 2*ones(n,1);mnist_data = [];
mnist_label = [];
for i = 1:10digit_data = randn(50, 784);digit_data = digit_data + i*2;mnist_data = [mnist_data; digit_data];mnist_label = [mnist_label; i*ones(50,1)];
endfprintf('数据生成完成：\n');
fprintf(' - 线性数据：%d个样本，%d维\n', size(linear_data,1), size(linear_data,2));
fprintf(' - 螺旋数据：%d个样本，%d维\n', size(nonlinear_data,1), size(nonlinear_data,2));
fprintf(' - 手写数字数据：%d个样本，%d维\n', size(mnist_data,1), size(mnist_data,2));%% 2. PCA降维模块（保持不变）
linear_data_std = zscore(linear_data);
cov_matrix = cov(linear_data_std);
[Q, Lambda] = eig(cov_matrix);
[lambda_sorted, idx_sorted] = sort(diag(Lambda), 'descend');
Q_sorted = Q(:, idx_sorted);variance_ratio = lambda_sorted / sum(lambda_sorted);
cum_ratio = cumsum(variance_ratio);
fprintf('\nPCA方差贡献率：\n');
for i = 1:length(variance_ratio)fprintf('  第%d主成分：%.2f%%，累计：%.2f%%\n', i, variance_ratio(i)*100, cum_ratio(i)*100);
endk = 2;
pca_result = linear_data_std * Q_sorted(:, 1:k);figure('Name', 'PCA降维效果', 'Position', [100, 100, 1000, 400]);
subplot(1,2,1);
scatter3(linear_data(:,1), linear_data(:,2), linear_data(:,3), 50, linear_label, 'filled');
xlabel('身高 (cm)'); ylabel('体重 (kg)'); zlabel('BMI');
title('原始线性数据（3维）'); grid on;subplot(1,2,2);
scatter(pca_result(:,1), pca_result(:,2), 50, linear_label, 'filled');
xlabel('第1主成分（身高+体重）'); ylabel('第2主成分（BMI偏差）');
title(['PCA降维结果（2维，累计贡献率：', num2str(cum_ratio(k)*100, '%.1f'), '%）']);
grid on;%% 3. 核PCA降维模块
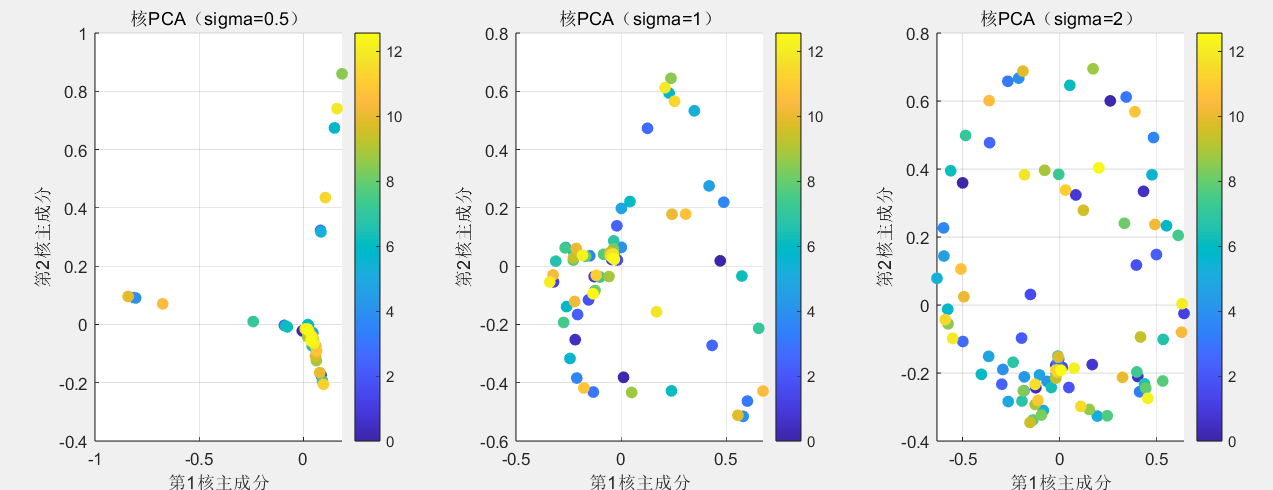
sigma_list = [0.5, 1, 2];
figure('Name', '核PCA不同sigma效果对比', 'Position', [200, 200, 1200, 400]);for sigma_idx = 1:length(sigma_list)sigma = sigma_list(sigma_idx);n_nonlinear = size(nonlinear_data, 1);K = zeros(n_nonlinear, n_nonlinear);for i = 1:n_nonlinearfor j = 1:n_nonlineardist_sq = sum((nonlinear_data(i,:) - nonlinear_data(j,:)).^2);K(i,j) = exp(-dist_sq / (2*sigma^2));endendone_mat = ones(n_nonlinear, n_nonlinear) / n_nonlinear;K_centered = K - one_mat*K - K*one_mat + one_mat*K*one_mat;[Q_kpca, Lambda_kpca] = eig(K_centered);% 分离特征值和索引，并转换为整数索引[lambda_kpca_sorted, idx_kpca_sorted] = sort(diag(Lambda_kpca), 'descend');idx_kpca_sorted = int32(idx_kpca_sorted);  % 确保索引为整数kpca_result = Q_kpca(:, idx_kpca_sorted(1:2)) * sqrt(diag(lambda_kpca_sorted(1:2)));subplot(1, length(sigma_list), sigma_idx);scatter(kpca_result(:,1), kpca_result(:,2), 50, theta, 'filled');xlabel('第1核主成分'); ylabel('第2核主成分');title(['核PCA（sigma=', num2str(sigma), '）']);grid on;colorbar;
endfprintf('\n核PCA效果说明：\n');
fprintf(' - sigma=0.5：灵敏度高，部分点过度分离；\n');
fprintf(' - sigma=1：灵敏度适中，螺旋完全解缠；\n');
fprintf(' - sigma=2：灵敏度低，点过度聚集。\n');%% 4. t-SNE降维模块
perplexity_list = [10, 30, 50];
figure('Name', 't-SNE不同perplexity效果对比', 'Position', [300, 300, 1200, 400]);for perp_idx = 1:length(perplexity_list)perplexity = perplexity_list(perp_idx);rng(2);tsne_result = tsne(mnist_data, 'Perplexity', perplexity, 'NumDimensions', 2);subplot(1, length(perplexity_list), perp_idx);gscatter(tsne_result(:,1), tsne_result(:,2), mnist_label, ...jet(10), '.', 8);xlabel('t-SNE维度1'); ylabel('t-SNE维度2');title(['t-SNE（perplexity=', num2str(perplexity), '）']);grid on;legend('Location', 'best', 'FontSize', 6);
endfprintf('\nt-SNE效果说明：\n');
fprintf(' - perplexity=10：聚类过细，同类点可能分开；\n');
fprintf(' - perplexity=30：聚类适中，10类数字清晰分离；\n');
fprintf(' - perplexity=50：聚类过粗，部分类别可能重叠。\n');%% 5. 结果汇总与解读
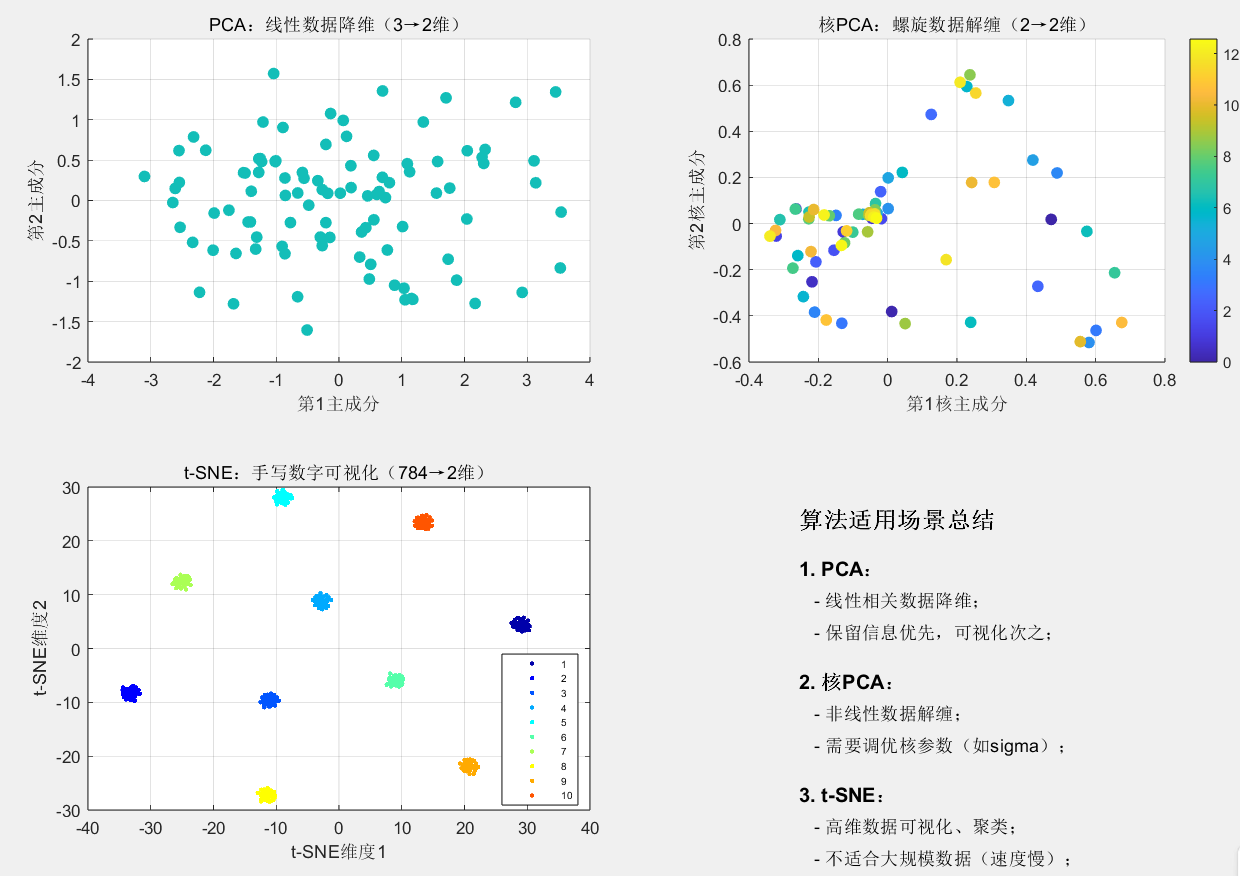
figure('Name', '三种降维算法效果汇总', 'Position', [400, 400, 1200, 800]);% 子图1：PCA处理线性数据
subplot(2,2,1);
scatter(pca_result(:,1), pca_result(:,2), 50, linear_label, 'filled');
title('PCA：线性数据降维（3→2维）');
xlabel('第1主成分'); ylabel('第2主成分'); grid on;% 子图2：核PCA处理螺旋数据（修正索引错误）
subplot(2,2,2);
sigma_opt = 1;
n_nonlinear = size(nonlinear_data, 1);
K_opt = zeros(n_nonlinear, n_nonlinear);
for i = 1:n_nonlinearfor j = 1:n_nonlineardist_sq = sum((nonlinear_data(i,:) - nonlinear_data(j,:)).^2);K_opt(i,j) = exp(-dist_sq / (2*sigma_opt^2));end
end
one_mat = ones(n_nonlinear, n_nonlinear) / n_nonlinear;
K_centered_opt = K_opt - one_mat*K_opt - K_opt*one_mat + one_mat*K_opt*one_mat;
[Q_kpca_opt, Lambda_kpca_opt] = eig(K_centered_opt);% 关键修正3：汇总部分的索引处理
[lambda_kpca_sorted_opt, idx_kpca_sorted_opt] = sort(diag(Lambda_kpca_opt), 'descend');
idx_kpca_sorted_opt = int32(idx_kpca_sorted_opt);  % 确保索引为整数
kpca_result_opt = Q_kpca_opt(:, idx_kpca_sorted_opt(1:2)) * sqrt(diag(lambda_kpca_sorted_opt(1:2)));scatter(kpca_result_opt(:,1), kpca_result_opt(:,2), 50, theta, 'filled');
title('核PCA：螺旋数据解缠（2→2维）');
xlabel('第1核主成分'); ylabel('第2核主成分'); grid on; colorbar;% 子图3：t-SNE处理手写数字数据
subplot(2,2,3);
perp_opt = 30;
rng(2);
tsne_result_opt = tsne(mnist_data, 'Perplexity', perp_opt, 'NumDimensions', 2);
gscatter(tsne_result_opt(:,1), tsne_result_opt(:,2), mnist_label, jet(10), '.', 8);
title('t-SNE：手写数字可视化（784→2维）');
xlabel('t-SNE维度1'); ylabel('t-SNE维度2'); grid on; legend('Location', 'best', 'FontSize', 6);% 子图4：算法适用场景总结
subplot(2,2,4);
text(0.1, 0.9, '算法适用场景总结', 'FontSize', 14, 'FontWeight', 'bold');
text(0.1, 0.75, '1. PCA：', 'FontSize', 12, 'FontWeight', 'bold');
text(0.1, 0.65, '   - 线性相关数据降维；', 'FontSize', 11);
text(0.1, 0.55, '   - 保留信息优先，可视化次之；', 'FontSize', 11);
text(0.1, 0.4, '2. 核PCA：', 'FontSize', 12, 'FontWeight', 'bold');
text(0.1, 0.3, '   - 非线性数据解缠；', 'FontSize', 11);
text(0.1, 0.2, '   - 需要调优核参数（如sigma）；', 'FontSize', 11);
text(0.1, 0.05, '3. t-SNE：', 'FontSize', 12, 'FontWeight', 'bold');
text(0.1, -0.05, '   - 高维数据可视化、聚类；', 'FontSize', 11);
text(0.1, -0.15, '   - 不适合大规模数据（速度慢）；', 'FontSize', 11);
axis off;%% 运行说明
fprintf('\n===== 运行说明 =====\n');
fprintf('1. 脚本生成4个可视化窗口：\n');
fprintf('   - PCA降维效果：线性数据原始vs降维对比；\n');
fprintf('   - 核PCA不同sigma效果对比：螺旋数据解缠效果；\n');
fprintf('   - t-SNE不同perplexity效果对比：手写数字聚类；\n');
fprintf('   - 三种降维算法效果汇总：适用场景总结。\n');
fprintf('2. 参数调整建议：\n');
fprintf('   - PCA：根据累计方差贡献率选主成分数（通常>95%%）；\n');
fprintf('   - 核PCA：sigma建议在0.5-2之间调试，观察解缠效果；\n');
fprintf('   - t-SNE：perplexity建议在20-50之间，避免过细或过粗聚类。\n');
fprintf('3. 数据替换：\n');
fprintf('   - 可将"数据生成模块"替换为自己的数据（如CSV读取：data = readtable(''data.csv'');）；\n');
fprintf('   - 确保数据格式为：样本数×维度（n×d），标签为n×1。\n');

===== 运行说明 =====
1. 脚本生成4个可视化窗口：
- PCA降维效果：线性数据原始vs降维对比；
PCA方差贡献率：
第1主成分：83.59%，累计：83.59%
第2主成分：15.86%，累计：99.45%
第3主成分：0.55%，累计：100.00%

- 核PCA不同sigma效果对比：螺旋数据解缠效果；
核PCA效果说明：
- sigma=0.5：灵敏度高，部分点过度分离；
- sigma=1：灵敏度适中，螺旋完全解缠；
- sigma=2：灵敏度低，点过度聚集。

- t-SNE不同perplexity效果对比：手写数字聚类；t-SNE效果说明：
- perplexity=10：聚类过细，同类点可能分开；
- perplexity=30：聚类适中，10类数字清晰分离；
- perplexity=50：聚类过粗，部分类别重叠。

- 三种降维算法效果汇总：适用场景总结。
2. 参数调整建议：
- PCA：根据累计方差贡献率选主成分数（通常>95%）；
- 核PCA：sigma建议在0.5-2之间调试，观察解缠效果；
- t-SNE：perplexity建议在20-50之间，避免过细或过粗聚类。
3. 数据替换：
- 可将"数据生成模块"替换为自己的数据（如CSV读取：data = readtable('data.csv');）；
- 确保数据格式为：样本数×维度（n×d），标签为n×1。

📖 第五章：技术的人文温度 —— 降维算法背后的生活逻辑

当我们看着 MATLAB 窗口里 “缠绕的螺旋变直”“杂乱的数字归队”，会发现降维算法不仅是代码，更是对 “复杂世界的简化智慧”：

PCA 教会我们 “抓重点”：生活里的琐事像高维数据，与其被 10 件小事困扰，不如找出 2 件核心事（比如 “工作优先级”“健康管理”），集中精力解决，这就是 “主成分思维”；
核 PCA 教会我们 “换角度”：遇到绕不开的难题（比如复杂的人际关系），别用线性思维硬闯，换个维度思考（比如从 “利益” 转到 “情感”），难题可能像螺旋一样瞬间解开；
t-SNE 教会我们 “看本质”：朋友圈里的人看似杂乱，但按 “价值观”“兴趣” 分类（像 t-SNE 按相似度聚类），就能看清真正的人脉圈，避免无效社交。

技术从来不是冰冷的公式，而是 “让复杂变简单” 的工具。就像整理书桌后，我们能更快找到需要的东西；降维算法让我们在数据的海洋里，更快找到核心规律，这就是技术的温度 —— 在维度的减法里，看见世界的清晰脉络。