数据结构之图（基本概念和模拟）

前言

我们在现实生活中常常有直线距离描述一个城市到另一个城市的距离，这样的结构是否可以在计算机中表示出来呢？

• 我们先抽象的表示两个城市之间的关系：

  
  我们将两个城市抽象成两个点，其中将他们之间的路径由一条线将他们连接起来。这样我们就可以抽象地表示城市A和城市B之间具有关系了。

那如果我们还有城市C、D、E呢？只有有关系，我们都可以链接进来描述他们之间的关系。

• 像这样描述顶点（城市）集合及顶点之间关系（路线）的结构我们称其为：图。
• 图是由顶点集合和边构成的 G = (V, E)。

下面，小编会和大家一起探讨图这样的数据结构的基本概念和存储结构。

1. 基本概念

图中的基本概念较多。

• 图是由顶点集合及顶点间的关系组成的一种数据结构：

  G = (V， E)，其中：顶点集合V = {x|x ∈ 对象集合}。集合V是有穷非空集合（简单来说就是有有限顶点）；边集合E = {(x, y) | x,y ∈ V} 或者 E = {<x, y>|x,y∈V && Path(x, y)}是顶点间关系的有穷集合。

  说明：

  • (x, y)表示x到y的一条双向通路，即(x, y)是无方向的。

  • Path(x, y)表示从x到y的一条单向通路，即Path(x, y)是有方向的。

1. 顶点和边：

   图中节点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。

2. 有向图和无向图：

   在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y, x>是两条不同的边，比如下图G3和G4为有向图。

   在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边，比如下图G1和G2为无向图。

   

   注意：无向边(x, y)等于有向边<x, y>和<y, x>。

3. 完全图：

   • 无向完全图：在有n个顶点的无向图中，若有$n\ast (n-1)/2$条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G1；

   • 有向完全图：在n个顶点的有向图中，若有$n\ast (n-1)$条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如上图G4。

4. 邻接顶点：

   • 在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；

   • 在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶
     点u，并称边<u, v>与顶点u和顶点v相关联。

5. 顶点的度：

   对于有向图而言：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和。

   其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。

   注意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。

6. 路径：

   在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。

7. 路径长度：

   对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和。

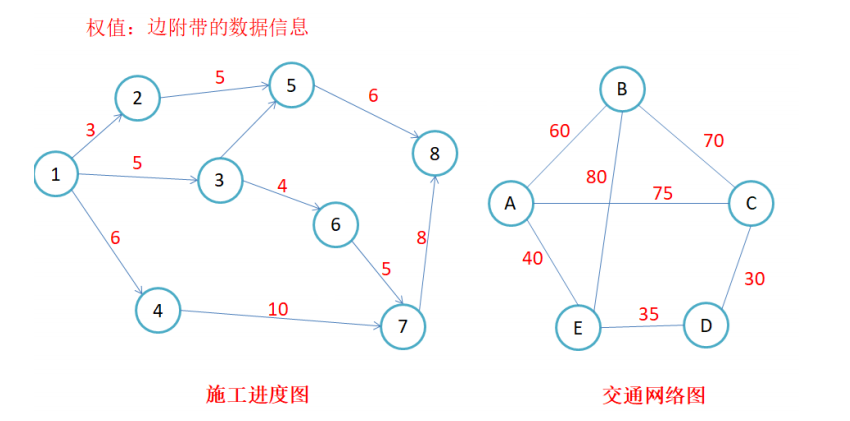
   • 权值：边附带的信息。例如：现在可以是城市A到城市B的花的时间、修路从城市A到城市B的成本。可以说：权值是由意义的。

     

8. 简单路径与回路：

   • 简单路径：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路
     径。

   • 回路/环路：若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环路（即没有重复路径的，能回到路径起点）

     

9. 子图：

   设图G = {V, E}和图G1={V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。即：子图的顶点和边都是原图的子集。

   

10. 连通图：

    在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的（连通是指由路径，而不是两个顶点之间相连），则称此图为连通图。

    • 强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图。

11. 生成树：

    一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。

上面我们把图的一些基本概念都说了，但是我们仍然对图的应用场景不是很了解，下面小编回列举一些图的应用场景：

1. 社交网络。例如，微信这样的强社交关系、抖音这样的弱社交关系。
2. 地图导航。
3. 互联网和推荐系统。
4. ……

2. 图的存储结构

因为图中既有节点，又有边(节点与节点之间的关系)。
因此，在图的存储中，只需要保存：节点和边关系即可。节点保存比较简单，只需要一段连续空间即可，那边关系该怎么保存呢？
图一共有两种存储结构：邻接矩阵、邻接表
下面我们一一介绍

2.1 邻接矩阵

因为顶点与顶点之间的关系就是连通与否，即为0或者1，因此邻接矩阵（二维数组）即是：先用一个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。

一般而言，我们都是以row作为起点，col作为终点。例如点(A, B)，我们一般是先找到行A，再找到列B。如下图，是两种图的存储结构（无向图、有向图）

• 如果我们想要表示权值，我们可以设置以个标志：例如NIL（设置的对应类型的一个默认值）。如果对应二维数组的值为NIL，则说明顶点A、B不连通；否则说明A、B联通，权值为G(A, B)。

• 优势：

  1. 邻接矩阵的存储方式非常适合稠密图。因为在邻接矩阵中，我们将任何一个顶点之间的关系都表示出来了。（对于无向图来说，大家可以了解无向图的压缩存储）

  2. 邻接矩阵判断两个顶点之间的关系/权值，时间复杂度为$O(1)$。

• 劣势：

  1. 邻接矩阵不适合稀疏图，太浪费空间了。

  2. 邻接矩阵判断与一个顶点有关系的顶点需要遍历，时间复杂度为$O(N)$。

下面我们尝试对邻接矩阵进行模拟：

namespace matrix
{// MAX_W：默认W权值的最大值// Direction：是否带方向template<class T, class W, W MAX_W = INT_MAX, bool Direction = false>class graph{/************ 初始化思路：* 邻接矩阵主要是用二维数组存储图结构* _vertexs：存储的是顶点集合。每一个顶点对应一个下标* _indexmap：顶点的数据类型可能不是整型，所以为了能够一个顶点能够表示二维数组的一个位置，我们采用map映射顶点类型和下标位置*  通过上面两个字段，我们能够顶点找下标、下标找顶点。* _matrix：二维数组，表示图结构。*************/private:vector<T> _vertexs;			//1、顶点集合map<T, size_t> _indexmap;	//2、顶点映射下标vector<vector<W>> _matrix;	//3、图边关系及权值public:graph() = default; //自动生成默认构造graph(const T* val, size_t n) //初始化一个邻接矩阵{_vertexs.reserve(n); //先预开空间for (size_t i = 0; i < n; ++i) //将顶点集合传入{_vertexs.push_back(val[i]); //顶点集合_indexmap[val[i]] = i;		//映射关系}// 图的边关系//--> 先开空间//开了空间但是size没有开上去_matrix.resize(n);for (size_t i = 0; i < n; ++i){_matrix[i].resize(n, MAX_W); //[]下标是以size为判断}}// 找到顶点对应下标size_t getvertexindex(const T& val){auto pos = _indexmap.find(val);if (pos != _indexmap.end()){return pos->second;}else{assert("顶点不存在");return -1;}}// 添加权值void addedge(const T& sour, const T& dest, const W& w){size_t poss = getvertexindex(sour);size_t posd = getvertexindex(dest);_matrix[poss][posd] = w;//无向图的处理if (Direction == false){_matrix[posd][poss] = w;}}// 打印void print(){for (size_t i = 0; i < _vertexs.size(); ++i){printf("[%zd]->", i);cout << _vertexs[i] << endl;}cout << endl;cout << "  ";for (size_t i = 0; i < _matrix.size(); i++){cout << i << " ";}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){cout << i << " ";for (size_t j = 0; j < _matrix[i].size(); ++j){if (_matrix[i][j] != MAX_W)cout << _matrix[i][j] << " ";elsecout << '*' << " ";}cout << endl;}}};
}

2.2 邻接表

邻接表的存储就比较之间了，存储的就是以一个与一个顶点相连的其它顶点。

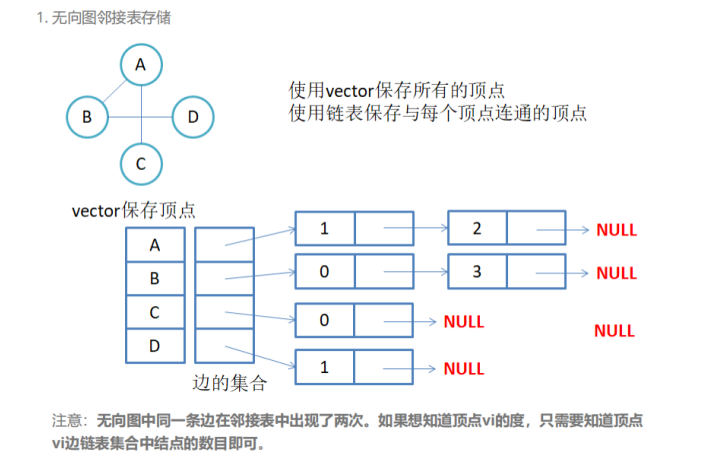
• 用数组代表顶点的集合，用链表表示边的关系。

  • 对于无向图来说，两个顶点之间有两条边关系。例如A到B、B到A。我们在无向图的邻接表存储中，只需要将两个边关系都存储如链表中即可

  

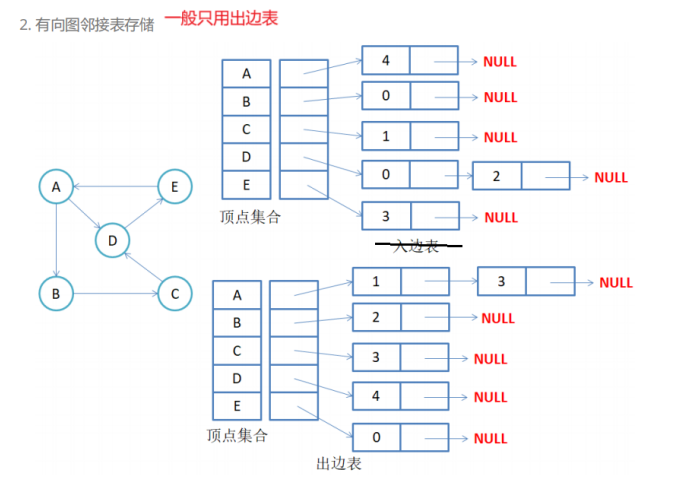
  • 对于有向图来说，两个顶点间的边有方向。所以为了描述一个图的有像关系，我们一般有两种表结构，一种是出边表（哪里能到这个顶点）、一个是入边表。一般出边表用的比较多。
    

• 如果是带有权值的边。那么我们就在链表的节点上添加权值即可。

1. 优势：

   • 适合用于稀疏图，不会浪费空间。但是会因为一些链接字段需要多余的空间。
   • 邻接矩阵判断与一个顶点有关系的顶点遍历是有效的，不会造成浪费。几乎就是$O(K)$

2. 劣势：

   • 不适合稠密图，关系比较多的图结构。
   • 判断两个顶点之间的权值需要遍历，时间复杂度为$O(N)$

下面我们尝试对邻接表进行模拟：

namespace table
{//邻接表的节点template<class W>struct Edge{W _w;Edge<W>* _next;size_t _dsti;Edge(const W& w, size_t dsti):_w(w), _dsti(dsti), _next(nullptr){}};template<class T, class W, bool Direction = false>class graph{typedef Edge<W> Edge;public:graph() = default; //自动生成默认构造graph(const T* val, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; ++i){_vertexs.push_back(val[i]); //顶点集合_indexmap[val[i]] = i;		//映射关系}_table.resize(n, nullptr);}// 找到顶点对应下标size_t getvertexindex(const T& val){auto pos = _indexmap.find(val);if (pos != _indexmap.end()){return pos->second;}else{assert("顶点不存在");return -1;}}// 添加权值 --> 例如：g -> ivoid addedge(const T& src, const T& dest, const W& w){size_t poss = getvertexindex(src);size_t posd = getvertexindex(dest);Edge* node = new Edge(w, posd);// 头插node->_next = _table[poss];_table[poss] = node;// 无向图if (Direction == false){Edge* node = new Edge(w, poss);// 头插node->_next = _table[posd];_table[posd] = node;}}// 打印void print(){size_t size = _vertexs.size();for (size_t i = 0; i < size; ++i){printf("[%zd]->", i);cout << _vertexs[i] << endl;}cout << endl;for (size_t i = 0; i < size; ++i){printf("[%zd]:", i);cout << _vertexs[i] << "-->";Edge* cur = _table[i];while (cur != nullptr){cout << "[" << cur->_dsti << ":" << _vertexs[cur->_dsti]<< " " << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}}private:vector<T> _vertexs;			//1、顶点集合map<T, size_t> _indexmap;	//2、顶点映射下标vector<Edge*> _table;	//3、图边关系及权值};}

• 总结：

  邻接矩阵和邻接表是一种优势互补的结构。我们需要根据实际场景选择对应的结构！

完。希望这篇文章能够帮助你！