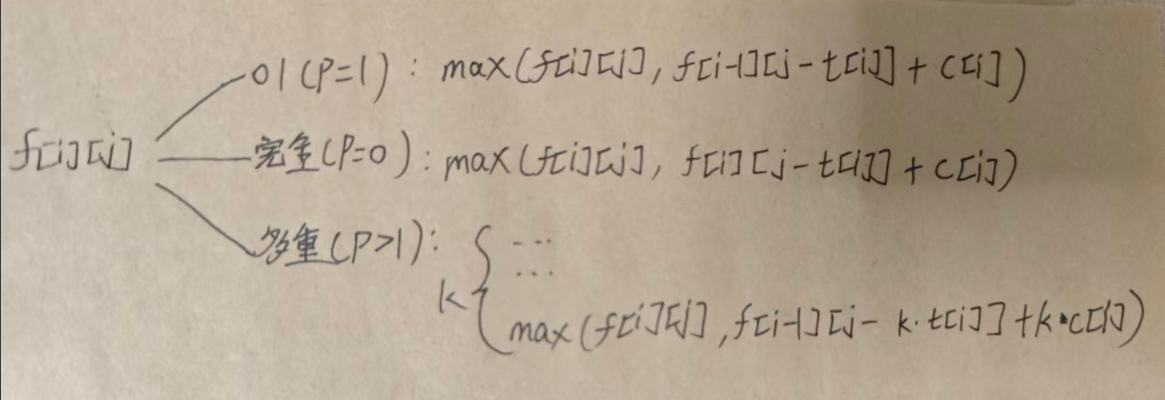算法题（225）：樱花

审题：
本题需要我们解决包含三种背包（01，完全，多重）的问题

思路：
方法一：混合背包动态规划

本题的背包类型是根据p值区分的，p为0时完全背包（无限次数），p为1时01背包（看一次），p大于1时多重背包（看多次）

（1）状态表示：
f[i][j]表示在前i棵树中看，保证使用时间不超过j的前提下，所欣赏到的最高美学价值

（2）状态转移方程：
我们可以根据p值不同来使用对应背包的状态转移方程

需要特别注意的就是他们的执行条件，01和完全背包只要注意j>=t[i]即可，多重背包要注意k<=p[i]且j>=k*t[i]

（3）初始化：
直接初始化为0即可

（4）填表顺序：
完全背包需要依赖当前行左侧，所以横向我们需要从小到大遍历，而所有背包都要依赖上一行，所以纵向需要从小到大遍历

（5）答案输出：
我们直接输出f[n][m]即可

（6）空间优化：

降维之后：
对于完全背包来说，需要保证横向从小到大填，保证前面（左侧）数据被更新

对于其他背包来说，需要保证横向从大到小填写，保证前面（左侧）数据不被更新

解题：
 

#include<iostream>
using namespace std;
const int N = 1e4+10, M = 1010;
int n,m;
int t[N], c[N], p[N];
int f[M];
int main()
{//数据预处理int t1, t2, t3, t4; char ch;cin >> t1 >> ch >> t2 >> t3 >> ch >> t4 >> n;m = (t3 * 60 + t4) - (t1 * 60 + t2);for (int i = 1; i <= n; i++){cin >> t[i] >> c[i] >> p[i];}//填表for (int i = 1; i <= n; i++){if (p[i] == 0)//完全{for (int j = t[i]; j <= m; j++){f[j] = max(f[j], f[j - t[i]] + c[i]);}}else {for (int j = m; j >= t[i]; j--){if (p[i] == 1)//01{f[j] = max(f[j], f[j - t[i]] + c[i]);}else//多重{for (int k = 1; k <= p[i] && j >= k*t[i]; k++){f[j] = max(f[j],f[j - k * t[i]] + k * c[i]);}}}}}cout << f[m] << endl;return 0;
}

P1833 樱花 - 洛谷