《强化学习数学原理》学习笔记5——压缩映射定理的证明

紧接着上一篇博客中贝尔曼最优方程的矩阵-向量形式：
$$v=f(v)\text{\hspace{1em}(1)}$$
为了分析式（1），首先需要介绍一下压缩映射定理（Contraction Mapping Theorem）。

一、先搞懂基础概念

在开始证明前，得先清楚两个关键概念：不动点和压缩映射。

（一）不动点

考虑一个函数 $f(x)$，其中 $x\in {\mathbb{R}}^d$，且 $f:{\mathbb{R}}^d\to {\mathbb{R}}^d$。如果有一个点 $x^{\ast }$，满足 $f(x^{\ast })=x^{\ast }$，那这个 $x^{\ast }$ 就被称为不动点。简单说，就是这个点经过函数映射后，结果还是它自己，所以叫不动点。

（二）压缩映射

如果存在一个 $\gamma \in (0,1)$，使得函数 $f$ 是压缩映射（也叫压缩函数），那么对于任意的 $x_1,x_2\in {\mathbb{R}}^d$，都有 $\Vert f(x_1)-f(x_2)\Vert \le \gamma \Vert x_1-x_2\Vert$。这里的 $\Vert \cdot \Vert$ 表示向量或者矩阵的范数。直观理解，就是函数 $f$ 把两个点 $x_1$ 和 $x_2$ 映射后的距离，比原来的距离“压缩”了，而且压缩比例不超过 $\gamma$（$\gamma$ 小于1）。

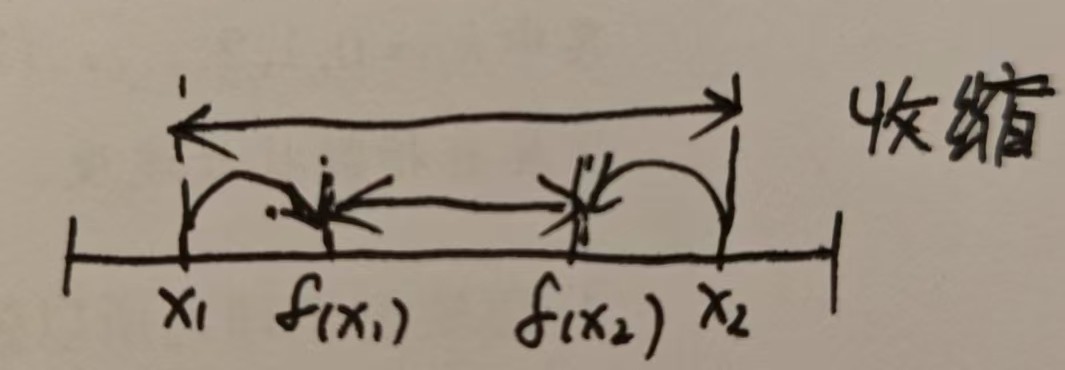
二、压缩映射定理

对于形如 $x=f(x)$ 的方程，其中 $x$ 和 $f(x)$ 都是实向量，如果 $f$ 是压缩映射，那么有以下性质：

1. 存在性：一定存在一个不动点 $x^{\ast }$，满足 $f(x^{\ast })=x^{\ast }$。
2. 唯一性：这个不动点 $x^{\ast }$ 是唯一的。
3. 算法性：考虑迭代过程
   $$x_{k+1}=f(x_k)\text{\hspace{1em}(2)}$$
   其中 $k=0,1,2,\dots$，对于任意初始值 $x_0$ （人为随意给定），当 $k\to \infty$ 时，$x_k\to x^{\ast }$，而且收敛速度是指数级的。

三、详细证明过程

证明分四个部分，咱们一步步来～

（一）证明迭代序列 {xk=f(xk−1)}k=1∞\{x_k = f(x_{k - 1})\}_{k = 1}^{\infty}{xk​=f(xk−1​)}k=1∞​是收敛的

要证明序列收敛，这里需要柯西序列的概念。柯西序列的定义是：如果一个序列 $x_1,x_2,\cdots \in \mathbb{R}$ 满足：对于任意小的 $\epsilon >0$，存在一个有限整数 $N$，使得任意 $m,n>N$ 时，都有 $\Vert x_m-x_n\Vert <\epsilon$，那么该序列被称为柯西序列。该条件的直观解释为， $N$ 之后的所有元素彼此足够接近。柯西序列的重要性在于，它保证了序列一定收敛到一个极限。

现在来证明 {xk=f(xk−1)}k=1∞\{x_k = f(x_{k - 1})\}_{k = 1}^{\infty}{xk​=f(xk−1​)}k=1∞​ 是柯西序列：
首先，因为 $f$ 是压缩映射，所以对于 $x_k=f(x_{k-1})$ 和 $x_{k-1}=f(x_{k-2})$，有
$$\Vert x_{k+1}-x_k\Vert =\Vert f(x_k)-f(x_{k-1})\Vert \le \gamma \Vert x_k-x_{k-1}\Vert \text{\hspace{1em}(3)}$$
类似地，$\Vert x_k-x_{k-1}\Vert \le \gamma \Vert x_{k-1}-x_{k-2}\Vert$，以此类推，$\Vert x_2-x_1\Vert \le \gamma \Vert x_1-x_0\Vert$。
所以可以递推得到：
$$\begin{array}{rl}\Vert x_{k+1}-x_k\Vert & \le \gamma \Vert x_k-x_{k-1}\Vert \\ & \le {\gamma }^2\Vert x_{k-1}-x_{k-2}\Vert \\ & ⋮\\ & \le {\gamma }^k\Vert x_1-x_0\Vert \end{array}\text{\hspace{1em}(4)}$$
因为 $\gamma <1$，所以对于任意的$x_0,x_1$，当 $k\to \infty$ 时，$\Vert x_{k+1}-x_k\Vert$ 会指数级地收敛到0。不过，光有 $\Vert x_{k+1}-x_k\Vert \to 0$ 还不足以证明序列 {xk}\{x_k\}{xk​} 收敛，所以得进一步考虑 $m>n$ 时的 $\Vert x_m-x_n\Vert$。
把 $\Vert x_m-x_n\Vert$ 拆成：
$$\Vert x_m-x_n\Vert =\Vert x_m-x_{m-1}+x_{m-1}-\cdots -x_{n+1}+x_{n+1}-x_n\Vert \text{\hspace{1em}(4)}$$
根据范数的三角不等式（即 $\Vert a+b\Vert \le \Vert a\Vert +\Vert b\Vert$），上式可以得到：
$$\Vert x_m-x_n\Vert \le \Vert x_m-x_{m-1}\Vert +\cdots +\Vert x_{n+1}-x_n\Vert \text{\hspace{1em}(5)}$$
再代入式（4）得到的 $\Vert x_{k+1}-x_k\Vert \le {\gamma }^k\Vert x_1-x_0\Vert$ ，就有：
$$\begin{array}{rl}\Vert x_m-x_n\Vert & \le {\gamma }^{m-1}\Vert x_1-x_0\Vert +\cdots +{\gamma }^n\Vert x_1-x_0\Vert \\ & ={\gamma }^n({\gamma }^{m-1-n}+\cdots +1)\Vert x_1-x_0\Vert \\ & \le {\gamma }^n(1+\gamma +\cdots +{\gamma }^{m-1-n}+{\gamma }^{m-n}+\cdots )\Vert x_1-x_0\Vert \end{array}\text{\hspace{1em}(6)}$$
而等比数列 $1+\gamma +{\gamma }^2+\cdots$ 的和是 $\frac{1}{1-\gamma }$（因为 $\gamma <1$），所以：
$$\Vert x_m-x_n\Vert \le \frac{{\gamma }^n}{1-\gamma }\Vert x_1-x_0\Vert \text{\hspace{1em}(7)}$$
上式表明，对于任意的 $\epsilon >0$，我们总能找到一个 $N$，使得当 $m,n>N$ 时，$\Vert x_m-x_n\Vert <\epsilon$。所以这个序列是柯西序列，必然收敛到一个极限点，记为 $x^{\ast }={\lim }_{k\to \infty }{x}_k$。

（二）证明极限 $x^{\ast }={\lim }_{k\to \infty }{x}_k$ 是不动点

因为 $\Vert f(x_k)-x_k\Vert =\Vert x_{k+1}-x_k\Vert \le {\gamma }^k\Vert x_1-x_0\Vert$，当 $k\to \infty$ 时，$\Vert f(x_k)-x_k\Vert$ 以指数级速度收敛到0。
又因为函数 $f$ 是连续的（压缩映射是连续的），所以对 $x_{k+1}=f(x_k)$ 两边取极限 $k\to \infty$，就有 ${\lim }_{k\to \infty }{x}_{k+1}={\lim }_{k\to \infty }f(x_k)$，也就是 $x^{\ast }=f(x^{\ast })$，所以 $x^{\ast }$ 是不动点。

（三）证明不动点是唯一的

假设存在另一个不动点 $x^{\prime }$，满足 $f(x^{\prime })=x^{\prime }$。
那么 $\Vert x^{\prime }-x^{\ast }\Vert =\Vert f(x^{\prime })-f(x^{\ast })\Vert$，因为 $f$ 是压缩映射，所以 $\Vert f(x^{\prime })-f(x^{\ast })\Vert \le \gamma \Vert x^{\prime }-x^{\ast }\Vert$。
也就是 $\Vert x^{\prime }-x^{\ast }\Vert \le \gamma \Vert x^{\prime }-x^{\ast }\Vert$。
因为 $\gamma <1$，要让这个不等式成立，只能是 $\Vert x^{\prime }-x^{\ast }\Vert =0$，所以 $x^{\prime }=x^{\ast }$，不动点唯一。

（四）证明 $x_k$ 指数级收敛到 $x^{\ast }$

回忆式（7）得到的 $\Vert x_m-x_n\Vert \le \frac{{\gamma }^n}{1-\gamma }\Vert x_1-x_0\Vert$。
因为 $m$ 可以任意大，当 $m\to \infty$ 时，
$$\Vert x^{\ast }-x_n\Vert =\underset{m\to \infty }{\lim }\Vert x_m-x_n\Vert \le \frac{{\gamma }^n}{1-\gamma }\Vert x_1-x_0\Vert \text{\hspace{1em}(8)}$$
又因为 $\gamma <1$，所以当 $n\to \infty$ 时，误差 $\Vert x^{\ast }-x_n\Vert$ 会指数级收敛到0。