当前位置：首页 > news >正文

树的遍历方式总结

news 2025/10/3 9:59:11

以此树为demo
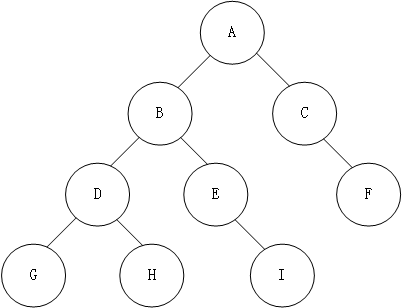
在这里插入图片描述

先序遍历

定义：优先访问根节点，然后访问左子树，最后访问右子树，根节点->左子树->右子树
按照定义，那么上述demo的结果可以很好得出来：A->B->D->G->H->E->I->C->F
那么算法怎么实现呢？这里使用递归方法：

public static void nlr(TreeNode rootNode) {TreeNode leftChild;TreeNode rightNode;if (rootNode != null) {System.out.print(rootNode.data+" ");leftChild = rootNode.leftChild;nlr(leftChild);rightNode = rootNode.rightChild;nlr(rightNode);}
}

运行结果如下：
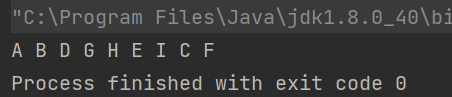
在这里插入图片描述

中序遍历

定义：优先访问左子树，然后访问根节点，然后访问右子树，左子树->根节点->右子树
按照定义，那么上述demo的结果可以很好得出来：G->D->H->B->E-I->A->C->F

public static void lnr(TreeNode rootNode) {TreeNode leftChild;TreeNode rightNode;if (rootNode != null) {leftChild = rootNode.leftChild;lnr(leftChild);System.out.print(rootNode.data+" ");rightNode = rootNode.rightChild;lnr(rightNode);}
}

运行结果如下：
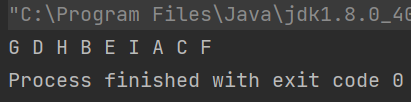
在这里插入图片描述

后续遍历

定义：优先访问左子树，然后访问右子树，然后访问根节点，左子树->右子树->根节点
按照定义，那么上述demo的结果可以很好得出来：G->H->D->I->E->B->F->C->A

public static void lrn(TreeNode rootNode) {TreeNode leftChild;TreeNode rightNode;if (rootNode != null) {leftChild = rootNode.leftChild;lrn(leftChild);rightNode = rootNode.rightChild;lrn(rightNode);System.out.print(rootNode.data+" ");}
}

运行结果如下：
在这里插入图片描述

按层遍历

定义：广度优先遍历，优先访问节点的左子树和右子树
使用队列方式来，每个节点判断一下有没有左右子树，有的话直接offer进队列，然后不停的输出队列即可

public static void storey(TreeNode rootNode) {//使用队列，先进先出Queue<TreeNode> queue = new LinkedList<>();queue.offer(rootNode);while (!queue.isEmpty()) {TreeNode t = queue.poll();System.out.print(t.data+" ");if (t.leftChild != null) {queue.offer(t.leftChild);}if (t.rightChild != null) {queue.offer(t.rightChild);}}
}

运行结果：
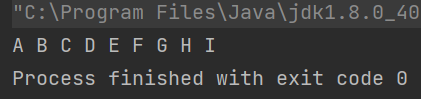
在这里插入图片描述

获取层数（获取二叉树最大深度）

相当于按层遍历的进阶了

public static void storey2(TreeNode rootNode) {//使用队列，先进先出Queue<TreeNode> queue = new LinkedList<>();queue.offer(rootNode);int n;int levelN =  1;int count = 0;System.out.print(rootNode.data);while (!queue.isEmpty()) {n = levelN;    //上一层的节点数量赋值给nlevelN = 0;   //清空leveN，开始重新计算当前行的节点数，给下一层使用System.out.println();for (int i=0;i<n;i++) {   //n表示这一行的所有节点数量，n的值依赖于上一层的levelN的值TreeNode t = queue.poll();if (t.leftChild != null) {queue.offer(t.leftChild);levelN++;   //节点数量+1System.out.print(t.leftChild.data+" ");}if (t.rightChild != null) {queue.offer(t.rightChild);levelN++;   //节点数量+1System.out.print(t.rightChild.data+" ");}}count++;   //开始换行}System.out.print("行数:"+count);
}

运行结果如下：
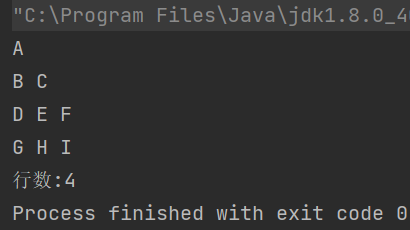
在这里插入图片描述
优化写法：leftchild和rightchild offer进队列的时候，不急着poll出来，等到当前层的所有节点的左右子树都offer进去的时候，再进行下一次循环，这时候队列数量就是当前层的节点数量，然后继续下一层遍历，本质上和上文写的逻辑一样，只不过不需要额外的变量了。

public static void storey2(TreeNode rootNode) {//使用队列，先进先出Queue<TreeNode> queue = new LinkedList<>();queue.offer(rootNode);int count = 0;System.out.print(rootNode.data);while (!queue.isEmpty()) {int n = queue.size();   //临时保存队列数量，队列数量就是当前层节点数量System.out.println();for (int i=0;i<n;i++) {   //循环当前层的节点数量TreeNode t = queue.poll();if (t.leftChild != null) {queue.offer(t.leftChild);System.out.print(t.leftChild.data+" ");}if (t.rightChild != null) {queue.offer(t.rightChild);System.out.print(t.rightChild.data+" ");}}count++;}System.out.print("行数:"+count);
}