算法基础 典型题 前缀和

算法基础练习总结入口：我的算法地图

一、基本概念

前缀和（Prefix Sum）：一种用于快速计算数组 / 矩阵中子区间和的预处理技术，核心是通过提前构建 “前缀和数组”，将原本需要 O (n) 时间的子区间和查询优化为 O (1)，大幅降低多次查询场景的时间复杂度。其思想简单但应用广泛，是数组、矩阵类问题的基础优化手段，主要分为一维前缀和和二维前缀和两大模式。

核心定义：对于序列（数组 / 矩阵），从 “起始位置” 到 “当前位置” 的累计和，称为该位置的前缀和。 例如，数组nums = [a1,
a2, a3, …, an]，其前缀和数组preSum满足preSum[i] = a1 + a2 + … + ai（通常preSum[0] = 0，方便边界计算）。

二、场景分析

模式 1：一维前缀和（适用于一维数组）
一维前缀和是基础，主要解决 “一维数组中子数组和的快速查询” 问题，如 “子数组和是否等于 K”“最大子数组和”（部分场景）等。

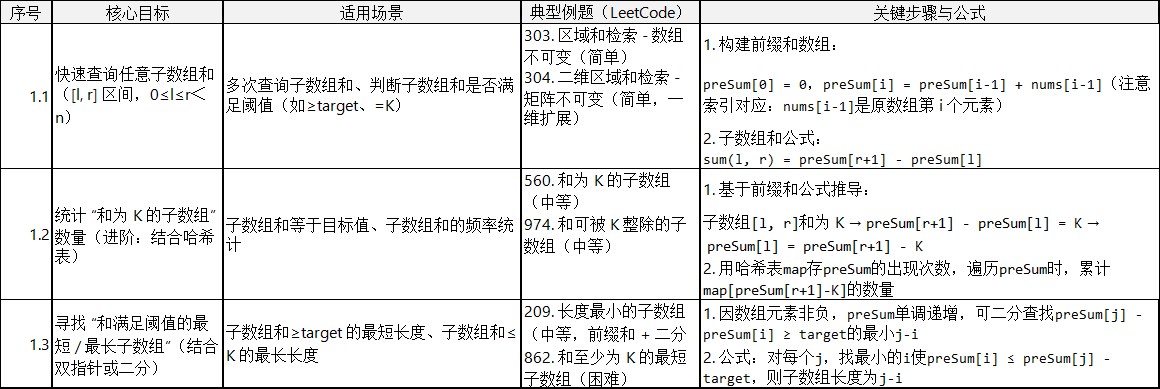
模式 2：二维前缀和（适用于二维矩阵）
二维前缀和是一维的扩展，用于快速计算 “二维矩阵中子矩阵的和”，如 “子矩阵和是否等于目标值”“最大子矩阵和” 等，核心是通过 “容斥原理” 构建前缀和矩阵。

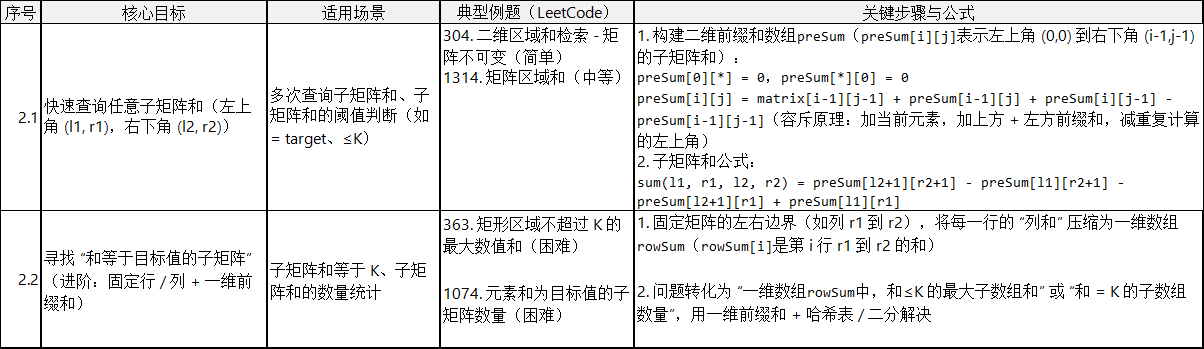
注意事项：
1）前缀和数组的初始化（边界处理）：通常将前缀和数组的长度设为 “原数组长度 + 1”（如preSum[0] = 0），避免计算sum(0, r)时出现preSum[r+1] - preSum[0]的边界判断，简化公式。例：原数组nums长度为 n，preSum长度为 n+1，preSum[i]对应nums[0…i-1]的和。
2）索引对应关系（避免越界）一维场景：preSum[i]对应原数组前 i 个元素（nums[0]到nums[i-1]），子数组[l, r]（原数组索引，0-based）的和是preSum[r+1] - preSum[l]。二维场景：preSum[i][j]对应矩阵(0,0)到(i-1,j-1)的和，子矩阵(l1, r1)到(l2, r2)（0-based）的和需用 “容斥公式”，注意不要漏加 / 漏减preSum[l1][r1]。
3）负数与单调性（影响二分适用性） ：若原数组包含负数，前缀和数组可能不单调，此时无法用 “二分查找” 优化（如 1.3 场景），需改用双指针（需数组非负）或哈希表（如 1.2 场景）。例：数组[-1, 2, 3]的前缀和为[0, -1, 1, 4]，非单调，二分查找会失效。
4）空间优化（可选） ：若仅需 “单次遍历 + 实时计算前缀和”（如 1.2 场景的和为 K 的子数组），可不用额外存储完整前缀和数组，而是用一个变量currentPreSum实时累加，配合哈希表存历史currentPreSum的出现次数，空间复杂度从 O (n) 降至 O (n)（哈希表仍需 O (n)，但减少了数组存储）。

三、典型题目

303. 区域和检索 - 数组不可变
给定一个整数数组 nums，处理以下类型的多个查询:计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right
实现 NumArray 类：NumArray(int[] nums) 使用数组 nums 初始化对象；int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + … + nums[right] )

class NumArray {
public:vector<int> prefixsum;// 定义前缀和数组prefixsum下标i为nums数组下标i之前数据的和NumArray(vector<int>& nums) {prefixsum.resize(nums.size() + 1); prefixsum[0] = 0;for (int i = 0; i < nums.size(); i++) {prefixsum[i + 1] = prefixsum[i] + nums[i];}}int sumRange(int left, int right) {return prefixsum[right + 1] - prefixsum[left];}
};

304. 二维区域和检索 - 矩阵不可变
给定一个二维矩阵 matrix，以下类型的多个请求：计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。实现 NumMatrix 类：NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化;int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

class NumMatrix {
public:vector<vector<int>> prefixsum;NumMatrix(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();prefixsum.resize(m, vector<int>(n + 1));prefixsum[0][0] = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {prefixsum[i][j + 1] = prefixsum[i][j] + matrix[i][j]; }}}int sumRegion(int row1, int col1, int row2, int col2) {int sum = 0;for (int i = row1; i <= row2; i++) {sum += prefixsum[i][col2 + 1] - prefixsum[i][col1];}return sum;}
};

560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。子数组是数组中元素的连续非空序列。

    int subarraySum(vector<int>& nums, int k) {// 思路：前缀和 加 hash表简化 解决// 定义前缀和数组 prefixSum[i]表示从数组起始位置到第i个位置的元素之和// 如果prefixSum[j] - prefixSum[i] = k，即从第i个位置到第j个位置的元素之和等于k，找到要求子数组// 通过遍历数组计算前缀和并用哈希表来存储每个前缀和出现次数，检查是否存在prefixSum[j] - k的前缀和unordered_map<int, int> prefixsummap;int count = 0;int prefixsum = 0;prefixsummap[0] = 1;for (int i = 0; i < nums.size(); i++)  {prefixsum += nums[i];if (prefixsummap.find(prefixsum - k) != prefixsummap.end()) {count += prefixsummap[prefixsum - k];}prefixsummap[prefixsum]++;}return count;}