当前位置：首页 > news >正文

【手撕机器学习 04】手撕线性回归：从“蒙眼下山”彻底理解梯度下降

news 2025/10/2 11:30:18

摘要：理论的终点是代码。本文将带你手撕第一个、也是最重要的机器学习算法——线性回归。我们将从“蒙眼下山”的生动比喻和可交互的流程图出发，让你彻底理解驱动现代AI的优化神器——梯度下降法的原理。然后，再用纯NumPy代码一步步实现它，并用动画展示模型“学习”的全过程。

前言：如何让电脑拥有“学习”的能力？

在上一篇 【手撕机器学习 03】 中，我们已经将“生数据”精心烹制成了“黄金特征”。现在，我们面临一个几乎是科幻领域的问题：

如何让一堆没有生命的0和1，拥有像人类一样的“学习”能力，能从经验（数据）中总结出规律？

答案，就隐藏在一个看似简单，却蕴含着深刻智慧的算法之中——梯度下降 (Gradient Descent)。它不是机器学习的全部，但它绝对是现代AI大厦那块最重要、最底层的基石。

本文将用最没有门槛的方式，带你彻底搞懂它，并亲手实现它。

一、核心思想：梯度下降的“蒙眼下山”五要素

忘掉所有数学，想象一个简单的游戏：你被空投到一座陌生的山上，眼睛被蒙住，任务是尽快走到山谷的最低点。

你该怎么办？答案简单得惊人：

你在哪？(当前位置)
- 你站在山坡的某个随机位置。这对应着我们模型参数（如w, b）的初始值。
你的目标是啥？(目标)
- 走到整座山的最低点。这个最低点，就是我们损失函数(Loss)的最小值，代表着模型的“完美状态”。
下一步往哪走？(方向)
- 伸出脚向四周探一探，找到坡度下降最快的方向。这个“最陡峭的方向”，在数学上有一个酷炫的名字——梯度(Gradient)的负方向。
走多远？(步长)
- 朝着那个方向，迈出一小步。这一步的大小，由**学习率(Learning Rate)**控制。步子太小，下山太慢，等到天荒地老；步子太大，你可能会一步迈过山谷，跑到对面的山坡上，永远无法到达最低点。
走多久？(迭代)
- 不断重复“探方向 -> 迈一步”的过程，重复很多很多次（由迭代次数Epochs决定），直到你感觉自己已经到了谷底。

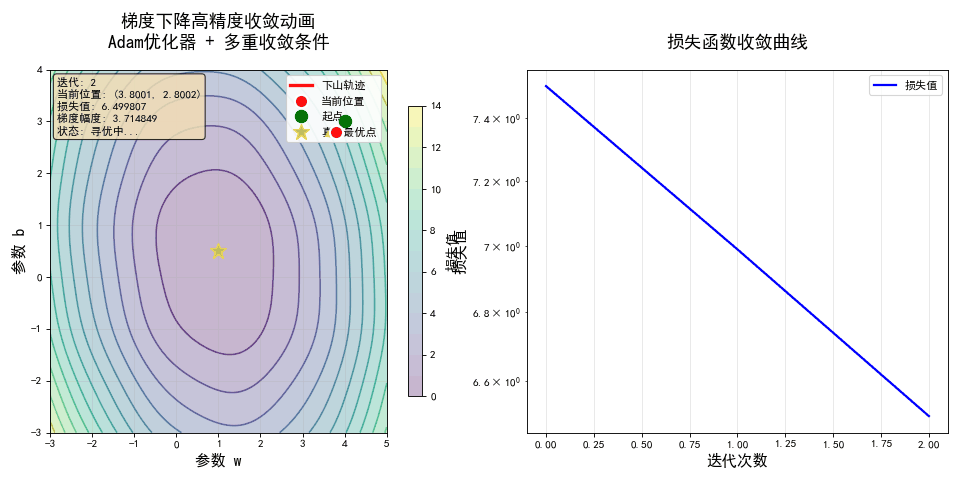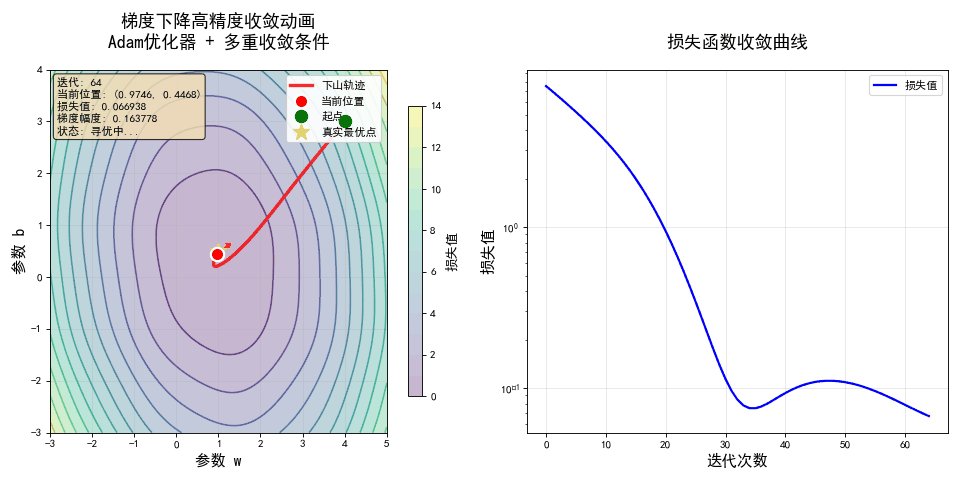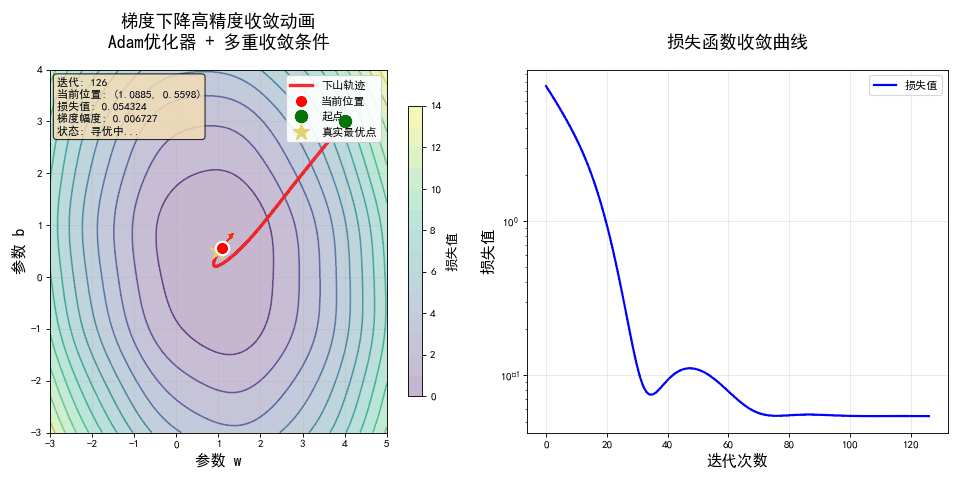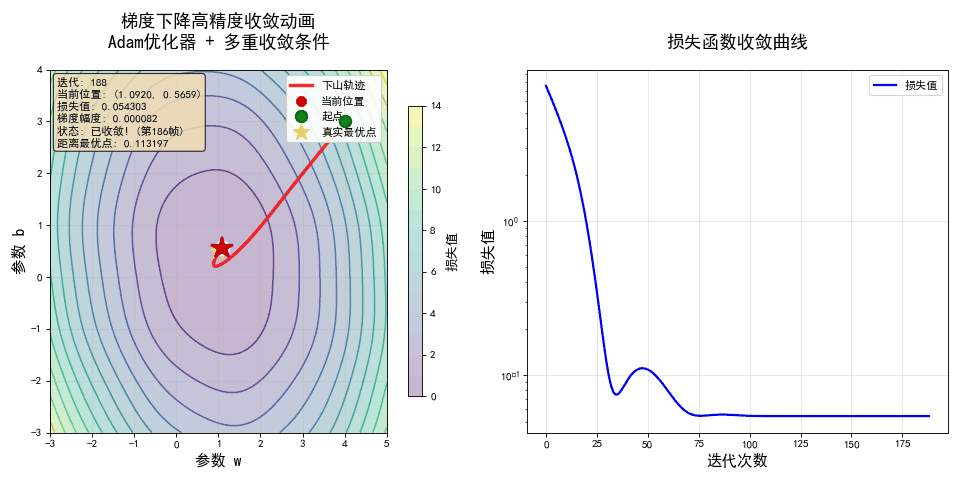
请添加图片描述

💡 这就是梯度下降法的全部！ 它把“寻找最优解”这个抽象问题，变成了一个简单、可执行的“下山”游戏。

二、蓝图解析：搭建一条“智能生产线”

现在，我们把“下山”游戏升级为一个更专业的比喻：建造一条“智能工厂”的“生产线”。

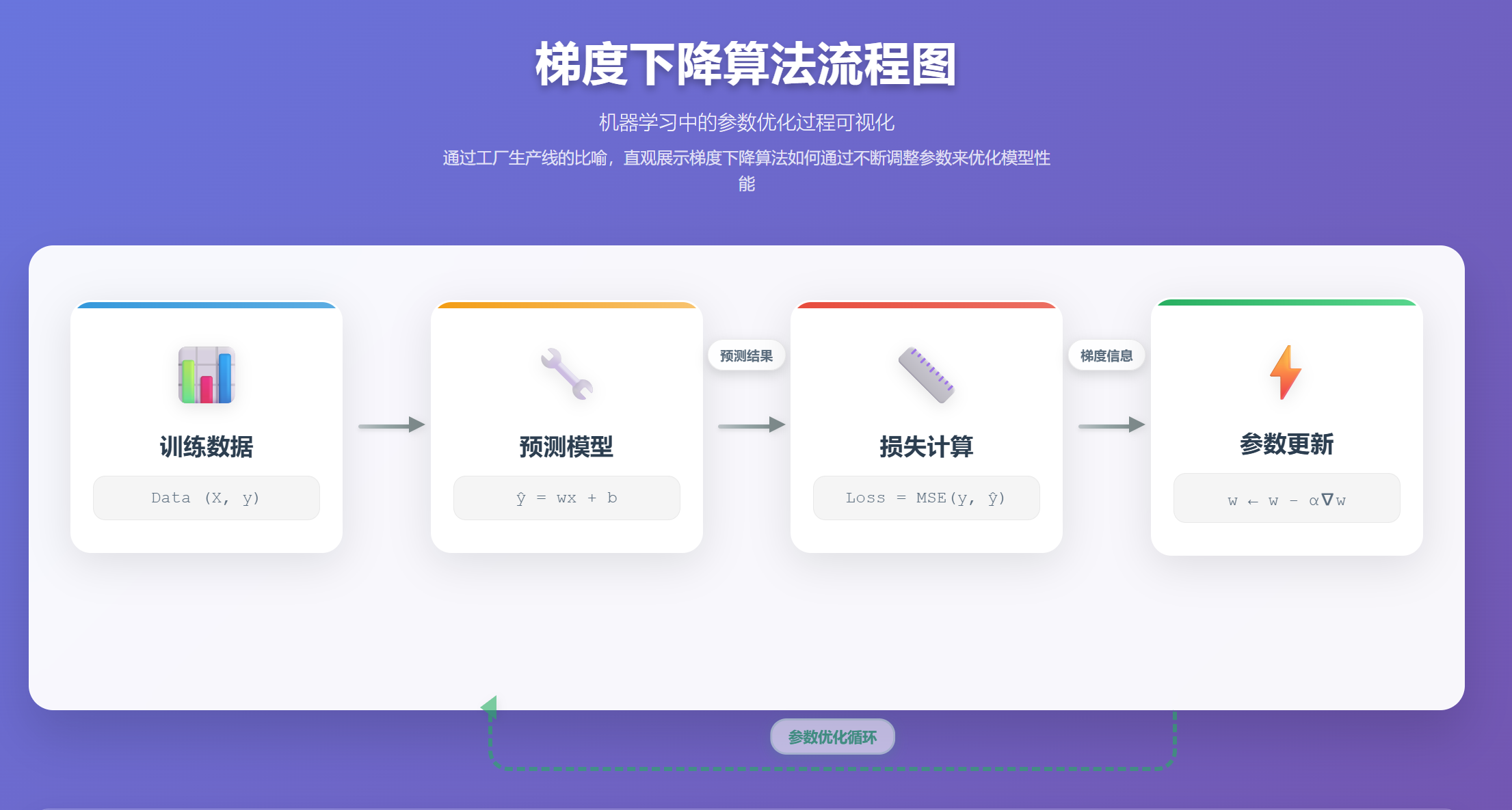
在这里插入图片描述

流程图解读：这就是我们整个梯度下降学习过程的宏观蓝图。原材料（数据）进入生产机器（模型），产出预测产品。质检部门（损失函数）对比产品和样板，生成一份质检报告（梯度）。总工程师（梯度下降）根据报告，回头去调校机器的旋钮（参数）。这个**“生产-质检-调校”**的循环，就是学习的本质。

让我们来详细解剖蓝图中的每一个关键部门。

2.1 质检部门 (损失函数)：如何衡量“好坏”？

我们的质检标准是均方误差 (Mean Squared Error, MSE)。

Loss = (1/n) * Σ (y_pred - y_true)²

让我们像庖丁解牛一样，彻底解剖这个公式：

(y_pred - y_true): 这是“误差”，即“预测值”与“真实值”的差距。这是所有衡量标准的核心。
(...)²: 这是“误差的平方”。
- 灵魂拷问：为什么是平方，而不是绝对值？
  - 首先，它们都能消除负号。但平方有一个绝妙的特性：它对大误差的惩罚远超小误差（10²=100, 2²=4）。这等于告诉模型：“犯小错可以容忍，但犯大错绝对不行！”
  - 其次，平方函数在数学上是处处可导的，且导函数形式简单，这为我们下一步计算“梯度”铺平了道路。
Σ (...): 这是“算总账”。把所有n个训练样本的“误差平方”都加起来，得到一个总的误差。
(1/n) * …: 这是“求平均”。把总误差除以样本数量n，得到“平均误差”。这确保了我们的“不合格率”标准不会因为工厂处理了更多订单（样本）而变得虚高。

2.2 总工程师的核心工具：梯度 (Gradient)

梯度是质检报告中最关键的信息，它告诉工程师如何调校旋钮。它包含两部分信息：

方向：梯度的正负号，告诉我们旋钮应该往大了拧，还是往小了拧。
大小：梯度的绝对值，告诉我们这次的偏差有多大，调整的“力度”应该有多强。

“人话”翻译梯度公式：

w的梯度 ≈ 平均( (预测值-真实值) * 房子面积 )
b的梯度 ≈ 平均( (预测值-真实值) )

💡 拔河比喻：
想象每个数据点都在“拉”这条直线，想让它靠近自己。

b的梯度，就是所有数据点“拉力”的平均值，决定了直线应该整体向上还是向下平移。
w的梯度，除了“拉力”，还乘以了一个X（房子面积）。这意味着，那些面积更大（离坐标轴更远）的点，拥有更大的“旋转力臂”，它们对直线的斜率调整有更大的“话语权”。这完全符合我们的直觉！

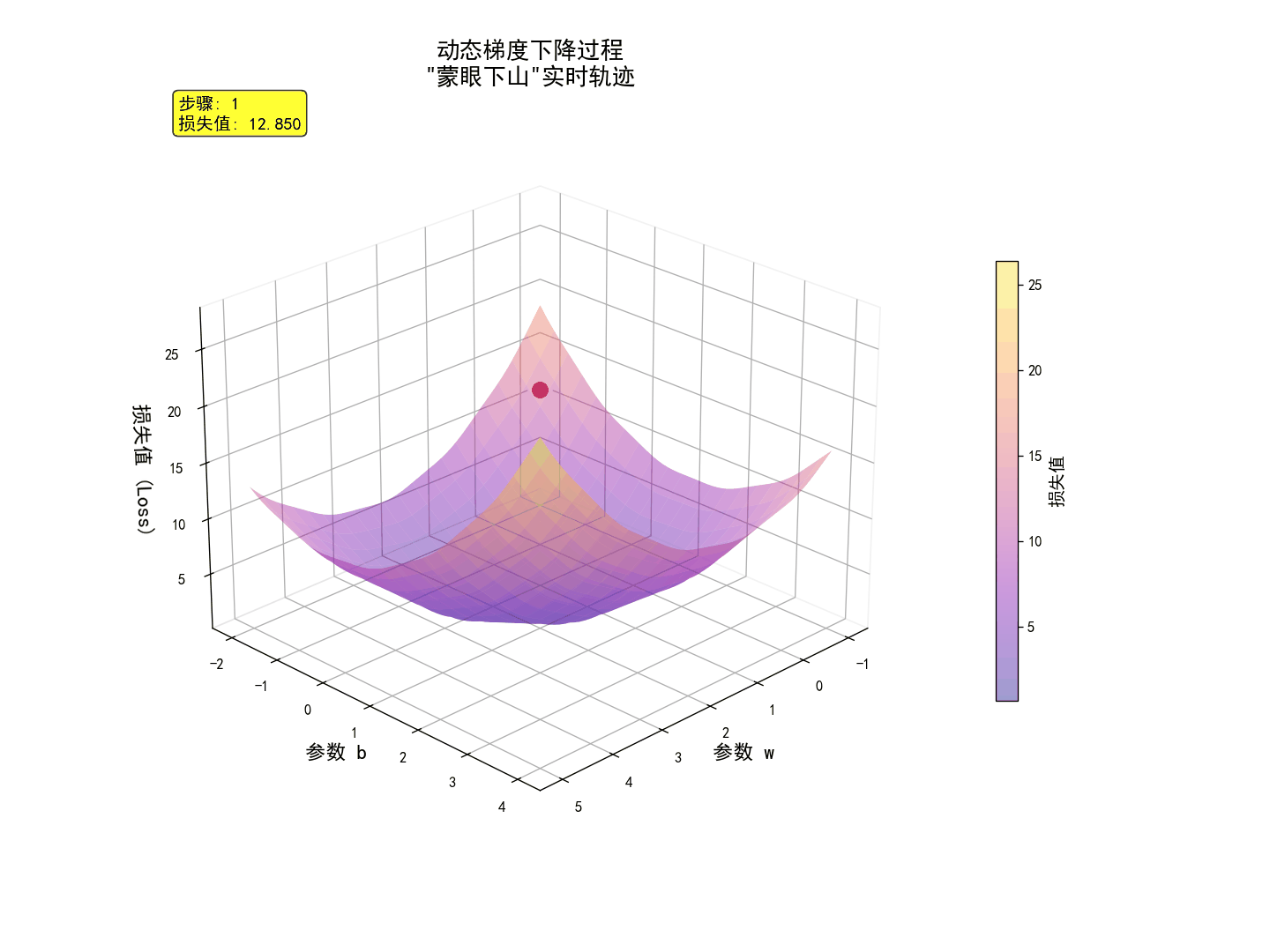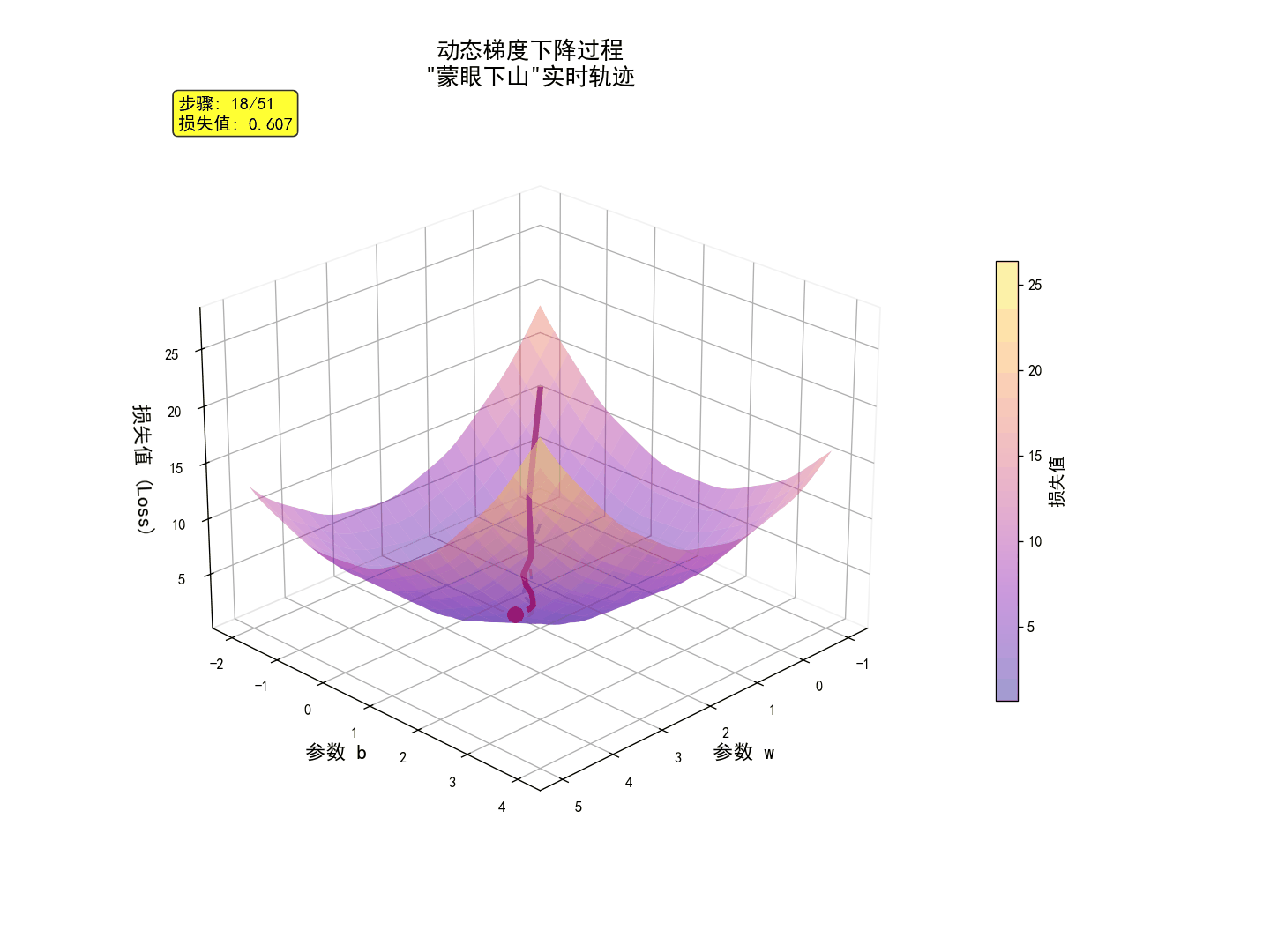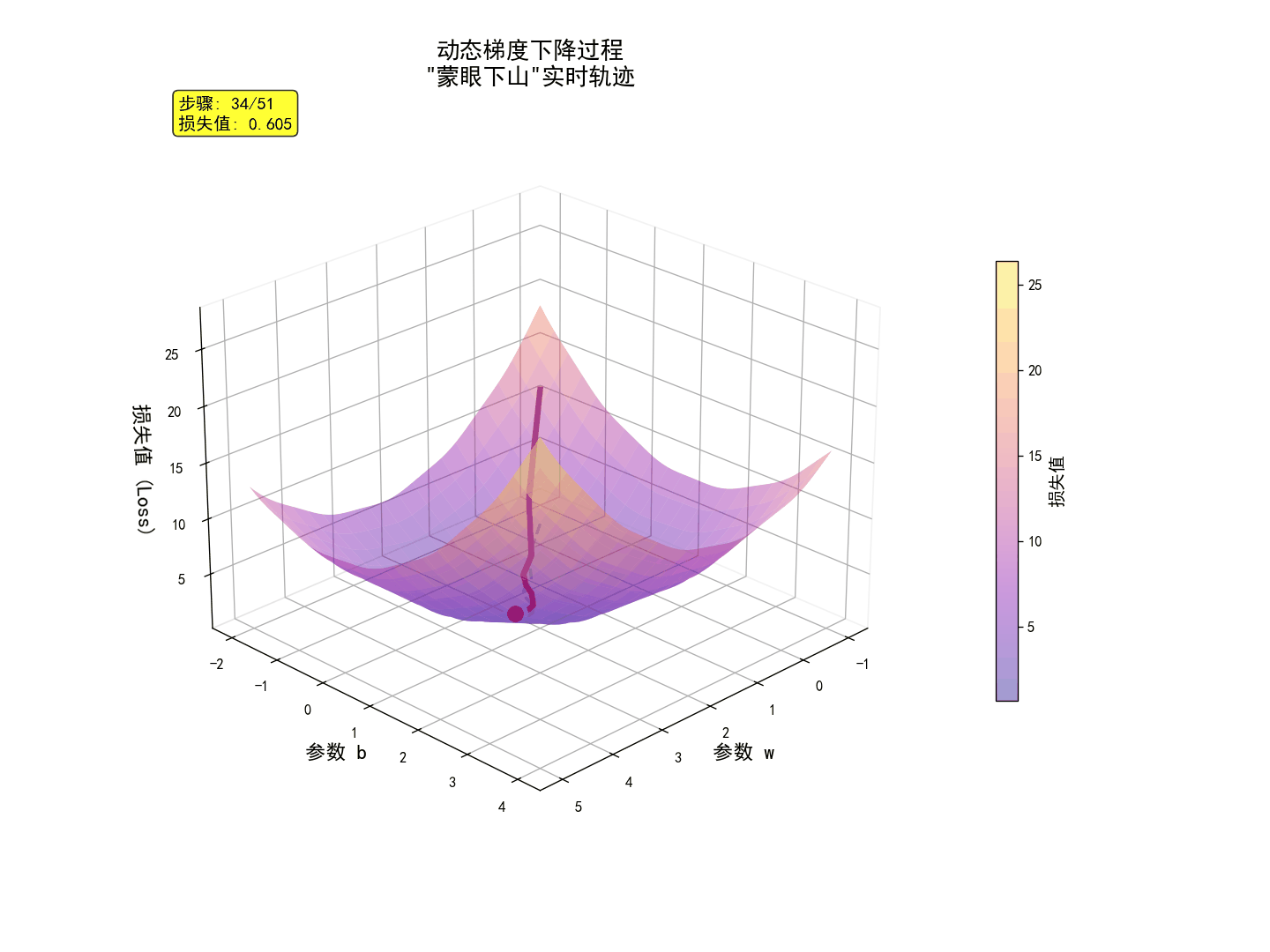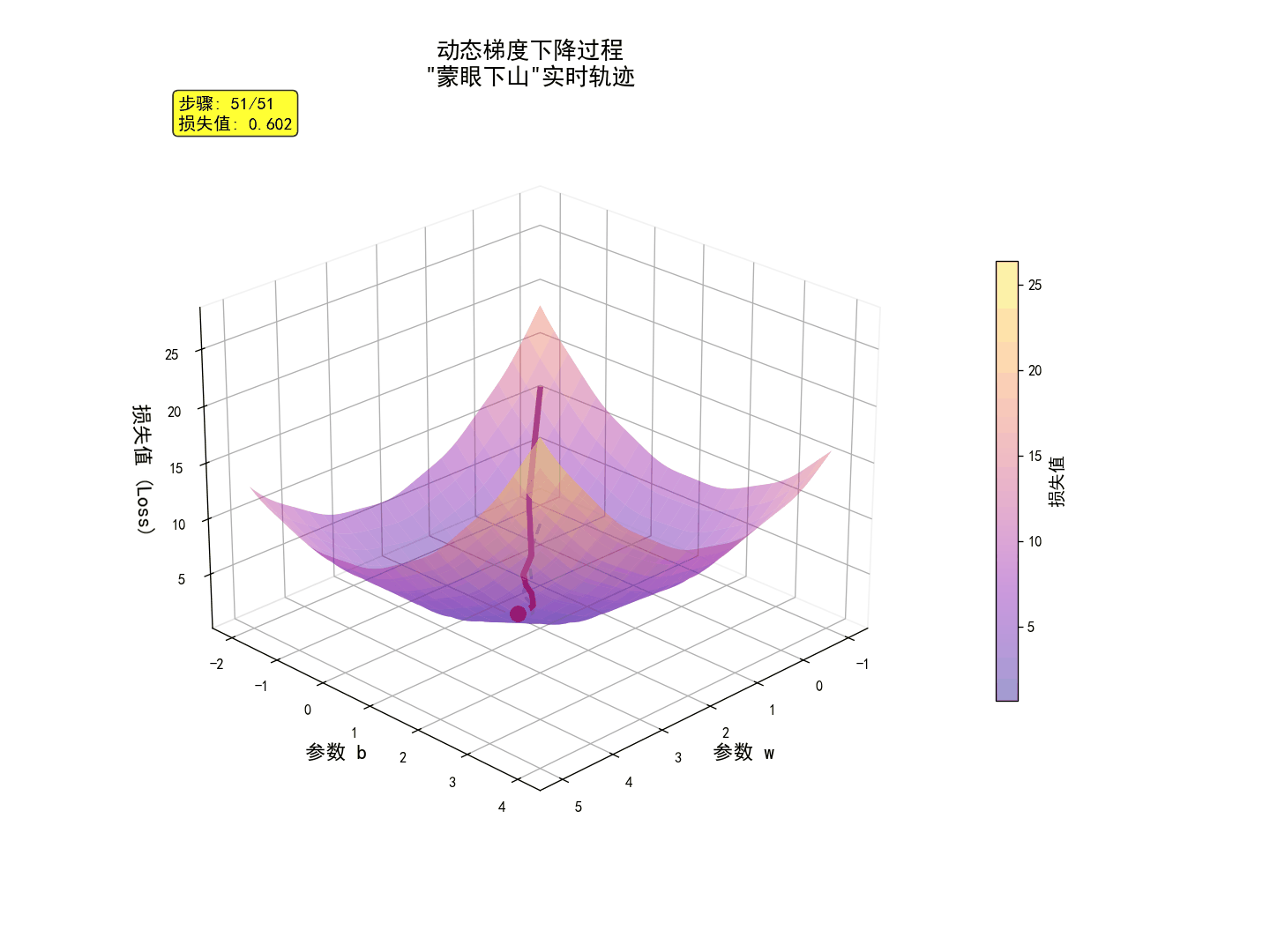
请添加图片描述

三、手撕代码：在代码中搭建生产线

理论已经无比清晰，现在让我们严格按照上面的“工程蓝图”，用代码将这条“智能生产线”搭建并运行起来。

import numpy as np
import matplotlib.pyplot as plt# --- 1. 原材料入库：准备数据 ---
# X: 房子面积, y: 真实价格
X = np.array([1, 2, 3, 4, 5])
y = np.array([3.1, 4.9, 7.2, 8.8, 11.1])# --- 2. 机器初始化：设定参数初始值 ---
# 我们的生产线刚出厂，旋钮w和b都先归零
w, b = 0.0, 0.0# --- 3. 设定生产规格：超参数 ---
learning_rate = 0.01 # 每次调校旋钮的幅度，工程师的“手感”
epochs = 1000        # 总共进行1000轮生产-调校循环
n = float(len(X))# --- 4. 启动生产线：梯度下降循环 ---
print("--- 生产线开始运行 ---")
for i in range(epochs):# a. 生产一个批次：用当前的w,b进行预测y_pred = w * X + b# b. 生成质检报告：根据公式计算梯度 (dw, db)#    这份报告精确地指明了w和b的“优化方向”和“力度”dw = (2/n) * np.sum((y_pred - y) * X)db = (2/n) * np.sum(y_pred - y)# c. 调校机器：总工程师根据报告，微调旋钮w -= learning_rate * dwb -= learning_rate * db# 打印生产线运行日志if (i+1) % 100 == 0:loss = np.mean((y_pred - y)**2) # QC部门报告当前“不合格率”print(f"第 {i+1} 轮生产, 不合格率(Loss): {loss:.4f}, w旋钮: {w:.4f}, b旋钮: {b:.4f}")# --- 5. 生产结束：展示最终调校好的机器参数 ---
print(f"\n✅ 生产线调校完成! 最佳参数: w = {w:.4f}, b = {b:.4f}")# 可视化最终产品的质量
plt.scatter(X, y, label='黄金样板')
plt.plot(X, w * X + b, color='red', label='最终模型生产线')
plt.legend()
plt.show()

四、对比Scikit-learn

我们亲手搭建了生产线，而scikit-learn则是一个全自动的“黑灯工厂”。

from sklearn.linear_model import LinearRegressionmodel = LinearRegression()
model.fit(X.reshape(-1, 1), y)print(f"\nScikit-learn的“黑灯工厂”结果 -> w: {model.coef_[0]:.4f}, b: {model.intercept_:.4f}")