拉格朗日乘子法

如何求极值?

• 给定函数：$z=f(x,y)$，如何求其极值点？
• 简单来说，直接求它的偏导即可，满足以下条件的点即为极值点候选：
  $f_x(x,y)=0,f_y(x,y)=0$

约束条件下的极值问题

现在问题难度加大：若函数存在约束条件，该如何求极值？
示例：已知长方体表面积固定，求其体积最大值。

• 体积函数（目标函数）：$V(x,y,z)=xyz$
• 表面积约束条件：$2xy+2yz+2zx=S$（$S$为固定表面积）

拉格朗日乘子法的核心原理

问题本质

• 若将目标函数$z=f(x,y)$看作“山峰的高度”，约束条件$g(x,y)=C$（$C$为常数）看作“镶嵌在山上的一条曲线”，则问题转化为：找到曲线上的最低点（或最高点）。
  

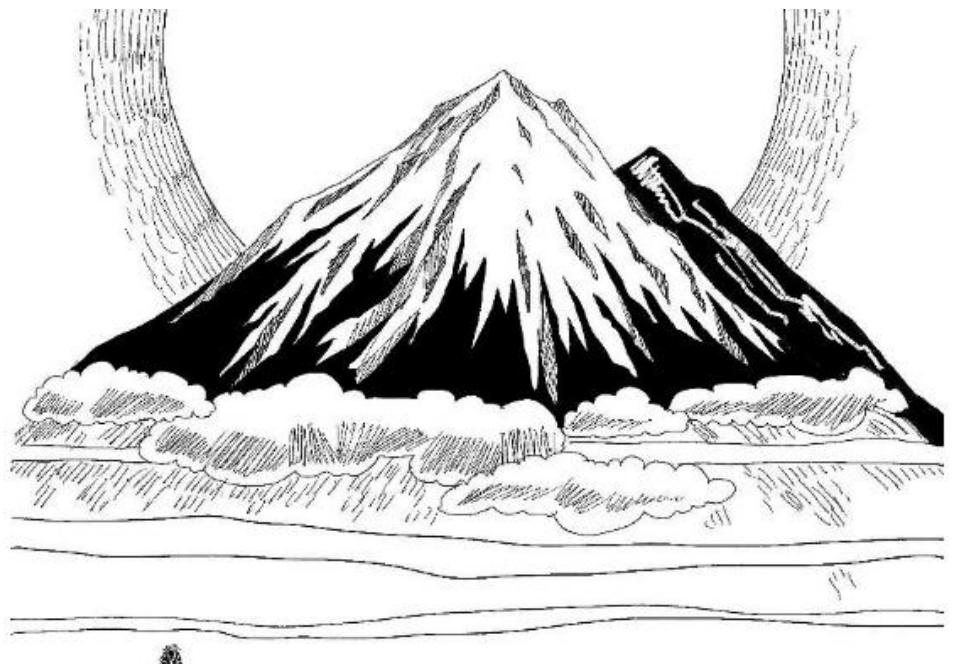
关键条件：法向量平行

曲线$g(x,y)=C$上的极值点，需满足目标函数的梯度与约束函数的梯度平行，即：
$\nabla f(x,y)=-\lambda \nabla g(x,y)$

其中：

• $\nabla$为梯度算子（$\nabla f=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$），
• $\lambda$为拉格朗日乘数（非零常数）。

等价变形

由$\nabla f(x,y)=-\lambda \nabla g(x,y)$可推得：
$\nabla (f(x,y)+\lambda g(x,y))=0$

约束极值的求解步骤

以“二元函数$z=f(x,y)$在约束条件$\phi (x,y)=0$下的极值”为例：

1. 构造拉格朗日函数
   引入拉格朗日乘数$\lambda$，构造新函数：
   $F(x,y)=f(x,y)+\lambda \phi (x,y)$

2. 求解偏导方程组
   对$F(x,y)$分别求关于$x$、$y$的偏导，并结合约束条件，联立方程组：
   $\{\begin{array}{l}{f}_x(x,y)+\lambda {\phi }_x(x,y)=0,\\ f_y(x,y)+\lambda {\phi }_y(x,y)=0,\\ \phi (x,y)=0\end{array}$

3. 确定极值点
   解上述方程组，得到的$(x,y)$即为目标函数在约束条件下的极值点候选。

多自变量与多约束条件下的拉格朗日乘子法

当自变量多于2个且约束条件多于1个时，方法可直接推广：

问题场景

• 目标函数：$u=f(x,y,z,t)$（4个自变量）
• 约束条件：$\phi (x,y,z,t)=0$、$\psi (x,y,z,t)=0$（2个约束）

求解步骤

1. 构造拉格朗日函数
   引入2个拉格朗日乘数${\lambda }_1$、${\lambda }_2$，构造函数：
   $F(x,y,z,t)=f(x,y,z,t)+{\lambda }_1\phi (x,y,z,t)+{\lambda }_2\psi (x,y,z,t)$

2. 求解偏导方程组
   对$F(x,y,z,t)$分别求关于$x$、$y$、$z$、$t$的偏导，并结合两个约束条件，联立方程组，解出的$(x,y,z,t)$即为极值点候选。

实例分析

实例1：三元函数的约束最大值

问题

已知函数$u=x^3{y}^{2}z$，约束条件为$x+y+z=12$（$x,y,z>0$），求$u$的最大值。

求解过程

1. 构造拉格朗日函数
   约束条件变形为$\phi (x,y,z)=x+y+z-12=0$，构造函数：
   $F(x,y,z)=x^3{y}^{2}z+\lambda (x+y+z-12)$

2. 求偏导并联立方程
   分别对$x$、$y$、$z$求偏导并令其为0，结合约束条件：
   $\{\begin{array}{l}{F}_x=3x^2{y}^{2}z+\lambda =0,\\ F_y=2x^{3}yz+\lambda =0,\\ F_z=x^3{y}^2+\lambda =0,\\ x+y+z=12\end{array}$

3. 求解极值点与最大值
   解方程组得唯一驻点$(6,4,2)$，代入目标函数得最大值：
   $u_{max}=6^3\cdot 4^2\cdot 2=6912$

实例2：椭球面切平面与最小体积四面体

问题

在第一卦限内作椭球面$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$的切平面，使切平面与三个坐标面所围成的四面体体积最小，求切点坐标。

求解过程

1. 设切点与切平面方程
   设椭球面上的切点为$P(x_0,y_0,z_0)$（$x_0>0,y_0>0,z_0>0$）。
   令$F(x,y,z)=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1$，则$F$在$P$点的偏导为：
   $F_x^{\prime }{|}_P=\frac{2x_0}{a^2}$，$F_y^{\prime }{|}_P=\frac{2y_0}{b^2}$，$F_z^{\prime }{|}_P=\frac{2z_0}{c^2}$。

   过$P$点的切平面方程为：
   $\frac{x_0}{a^2}(x-x_0)+\frac{y_0}{b^2}(y-y_0)+\frac{z_0}{c^2}(z-z_0)=0$

   结合椭球面方程$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}=1$，化简切平面方程为：
   $\frac{x\cdot x_0}{a^2}+\frac{y\cdot y_0}{b^2}+\frac{z\cdot z_0}{c^2}=1$

2. 求切平面在坐标轴上的截距
   切平面与$x$、$y$、$z$轴的截距分别为：
   $x=\frac{a^2}{x_0}$，$y=\frac{b^2}{y_0}$，$z=\frac{c^2}{z_0}$

3. 确定目标函数（四面体体积）
   切平面与三个坐标面围成的四面体体积为：
   $V=\frac{1}{6}\cdot x\cdot y\cdot z=\frac{a^2{b}^2{c}^2}{6x_0{y}_0{z}_0}$

   由于$a^2{b}^2{c}^2$、$6$为常数，最小化$V$等价于最大化$x_0{y}_0{z}_0$，故可令目标函数为$u=\ln x_0+\ln y_0+\ln z_0$（对数函数单调递增，最大化$u$即最大化$x_0{y}_0{z}_0$）。

4. 构造拉格朗日函数并求解
   约束条件为$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}-1=0$，构造拉格朗日函数：
   $L(x_0,y_0,z_0)=\ln x_0+\ln y_0+\ln z_0+\lambda \left(\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}-1\right)$

   对$x_0$、$y_0$、$z_0$求偏导并令其为0，结合约束条件：
   $\{\begin{array}{l}{L}_{x_0}^{\prime }=\frac{1}{x_0}+\lambda \cdot \frac{2x_0}{a^2}=0,\\ L_{y_0}^{\prime }=\frac{1}{y_0}+\lambda \cdot \frac{2y_0}{b^2}=0,\\ L_{z_0}^{\prime }=\frac{1}{z_0}+\lambda \cdot \frac{2z_0}{c^2}=0,\\ \frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}=1\end{array}$

   解方程组得切点坐标：
   $x_0=\frac{a}{\sqrt{3}}$，$y_0=\frac{b}{\sqrt{3}}$，$z_0=\frac{c}{\sqrt{3}}$

最终结论

使四面体体积最小的切点坐标为：$\left(\frac{a}{\sqrt{3}},\frac{b}{\sqrt{3}},\frac{c}{\sqrt{3}}\right)$