快速傅里叶变换分析频谱详解及python代码示例

一、快速傅里叶变换简介

在信号分析处理领域中，法国数学家傅里叶提出的傅里叶变换理论被广泛使用，该理论的核心思想可概括为：在一定条件下，任何一个复杂函数可以表示为不同频率的正弦函数之和。

傅里叶变换又分为连续傅里叶变换和离散傅里叶变换，其中离散傅里叶变换（Discrete Fourier Transform，DFT）主要用于处理对真实世界取样得到的离散信号。

由于DFT计算效率较慢，如果要应用到实际信号分析中就必须提高其运算速度，由此快速傅里叶变换（Fast Fourier Transform，FFT）被提出。

有关FFT的原理介绍及完整代码实现，可见本博客另一篇文章快速傅里叶变换简介及python实现。

二、复合频率信号生成

2.1复合频率信号

复合频率信号是指不同频率的正弦信号叠加在一起形成的信号，以此作为频谱分析的对象对FFT频谱分析进行介绍和验证。

本节使用了3种频率的正弦信号相加，主要是使用python的numpy软件包生成信号序列。

2.2代码实现及效果图

python代码如下：

f1 = 50
f2 = 70
f3 = 90
t = 0.1
fs = 2000
N = int(t * fs)
n = np.arange(N)y1 = np.sin(2 * np.pi * f1 * n / fs)
y2 = 2*np.sin(2 * np.pi * f2 * n / fs)
y3 = np.sin(2 * np.pi * f3 * n / fs)
y = y1 + y2 + y3
plt.figure(figsize=(12, 8))plt.subplot(4, 1, 1)
plt.plot(y1, linewidth=0.5)
plt.title(f'{f1}Hz')plt.subplot(4, 1, 2)
plt.plot(y2, linewidth=0.5)
plt.title(f'{f2}Hz')plt.subplot(4, 1, 3)
plt.plot(y3, linewidth=0.5)
plt.title(f'{f3}Hz')plt.subplot(4, 1, 4)
plt.plot(y, linewidth=0.5)plt.tight_layout()
plt.show()

代码执行效果如下图：

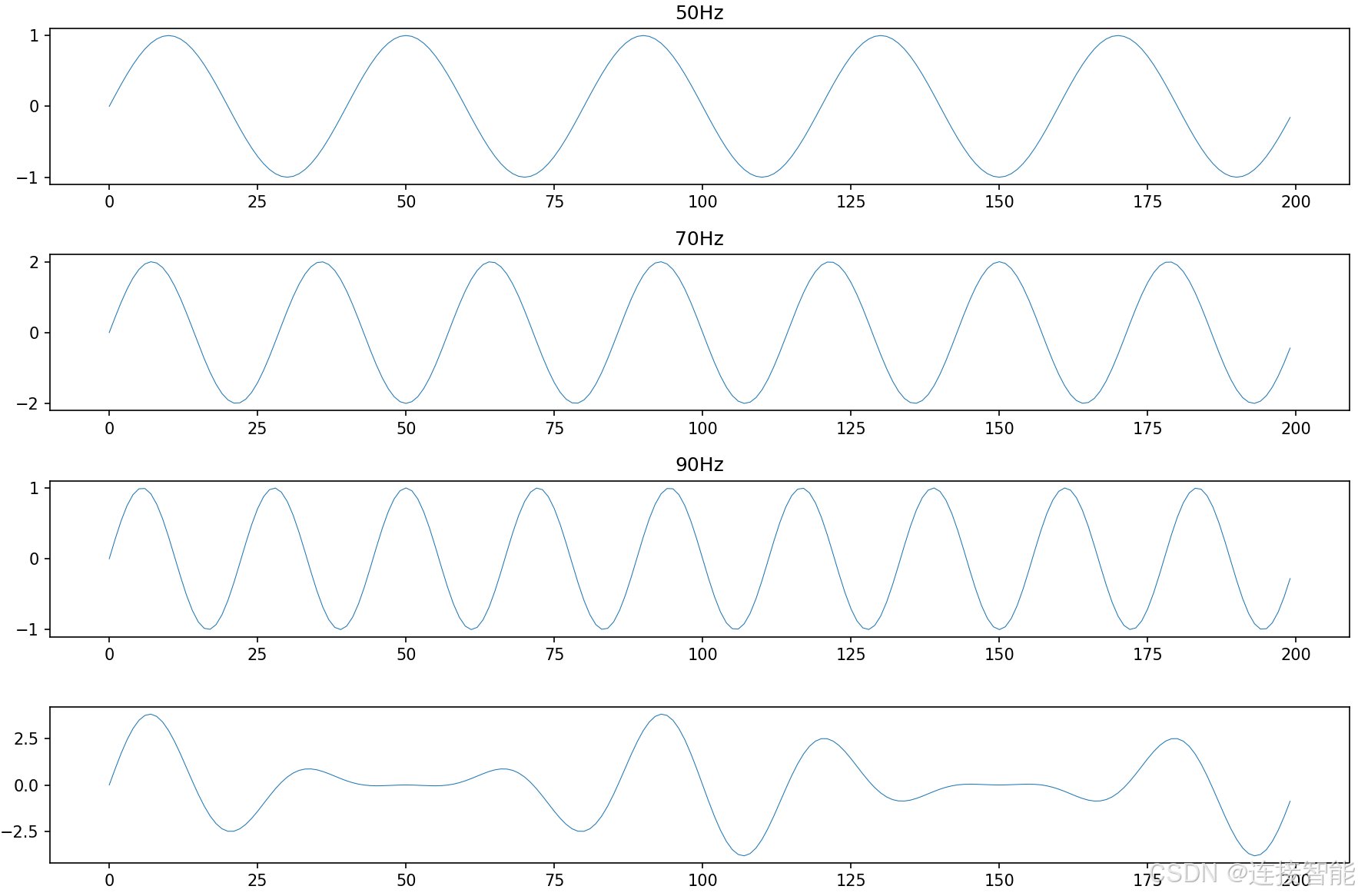
上面三图分别是不同频率下的正弦信号，最下面图是三个正弦信号相加的结果图。

2.3代码说明

1. 代码中f1、f2、f3为不同的频率变量，t为采样时间，fs为采样频率，N即为总的采样点数；
2. y1、y2、y3为对应频率下的正弦信号序列，使用numpy的sin函数实现；
3. y1、y3的振幅为1，而y2的振幅为2，设置不同振幅的目的是验证FFT分析结果是否正确；
4. y是y1、y2、y3相加的结果，也是最终的复合频率信号序列；
5. 代码最后使用matplotlib包将四个信号序列绘制出来

三、FFT频谱分析

3.1频谱分析目的

FFT频谱分析的目的有两个：

1. 得出信号的频率组成；
2. 得出不同频率信号对应的振幅

3.2代码实现及效果图

python代码如下：

freqs = np.fft.fftfreq(N, 1/fs)[:N//2]
fft_y = np.fft.fft(y)[:N//2]
print(len(fft_y))
plt.figure(figsize=(12, 8))
plt.plot(freqs, np.abs(fft_y)/N*2, linewidth=0.5)
plt.grid(True)
# plt.xlim(0, 200)
plt.tight_layout()
plt.show()

代码执行效果如下图：

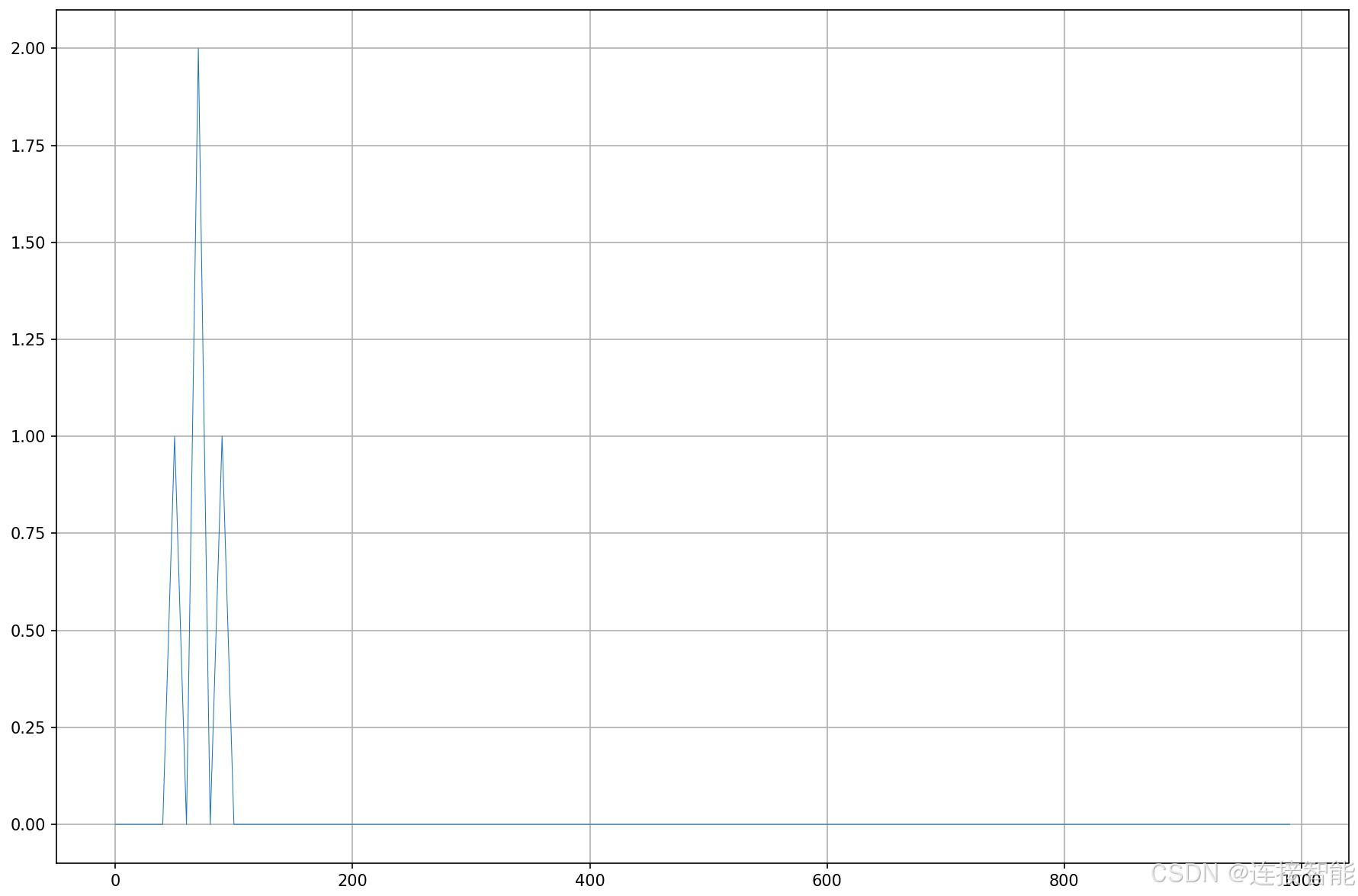
由于采样频率为2000Hz，所以图中横坐标最右端为1000Hz，即最大频率是奈奎斯特频率：fs/2，所以图片右端有一大段空白。

可以通过plt.xlim函数设置横坐标范围，例如设置为0~200，如下图所示：

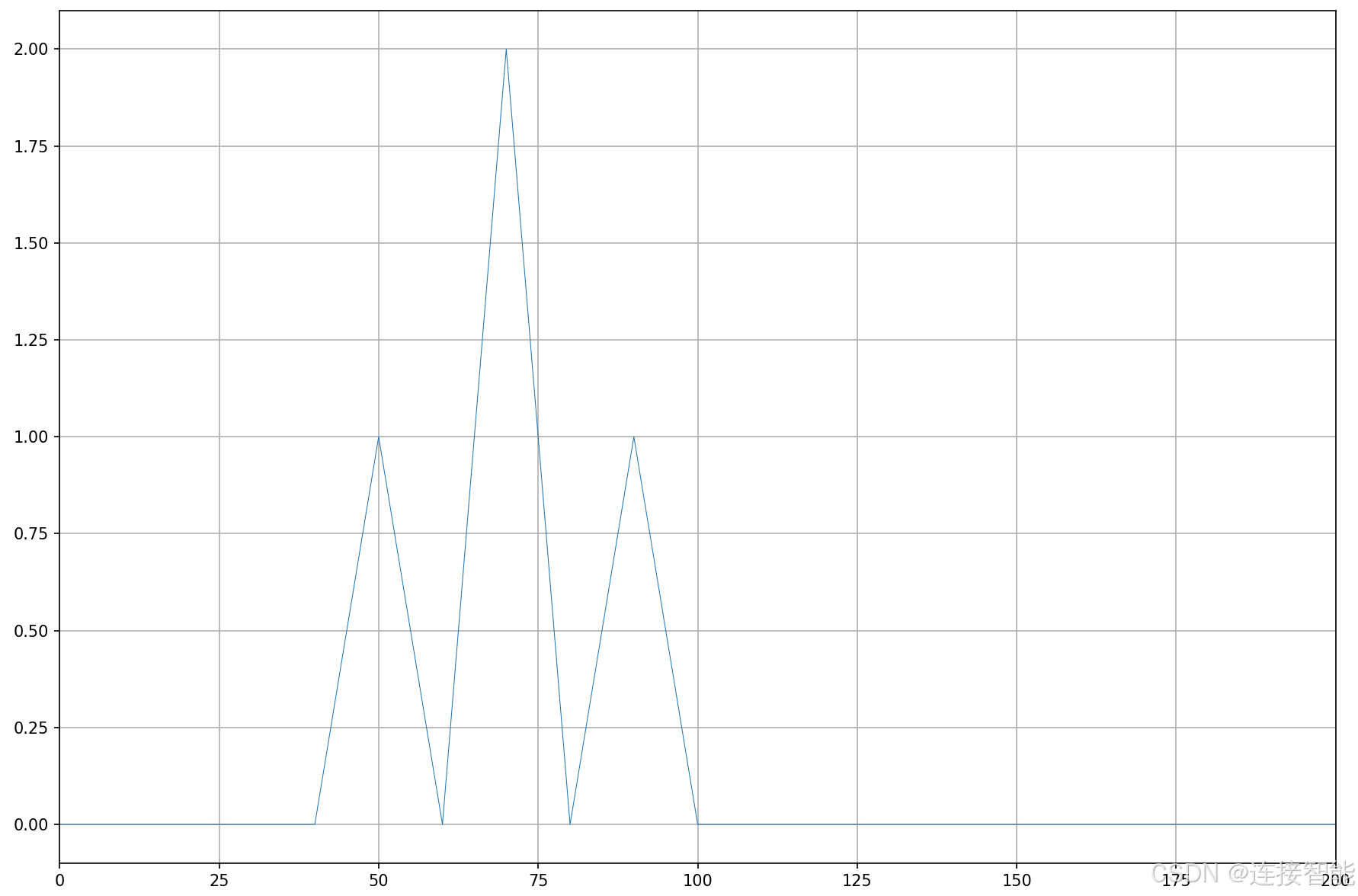
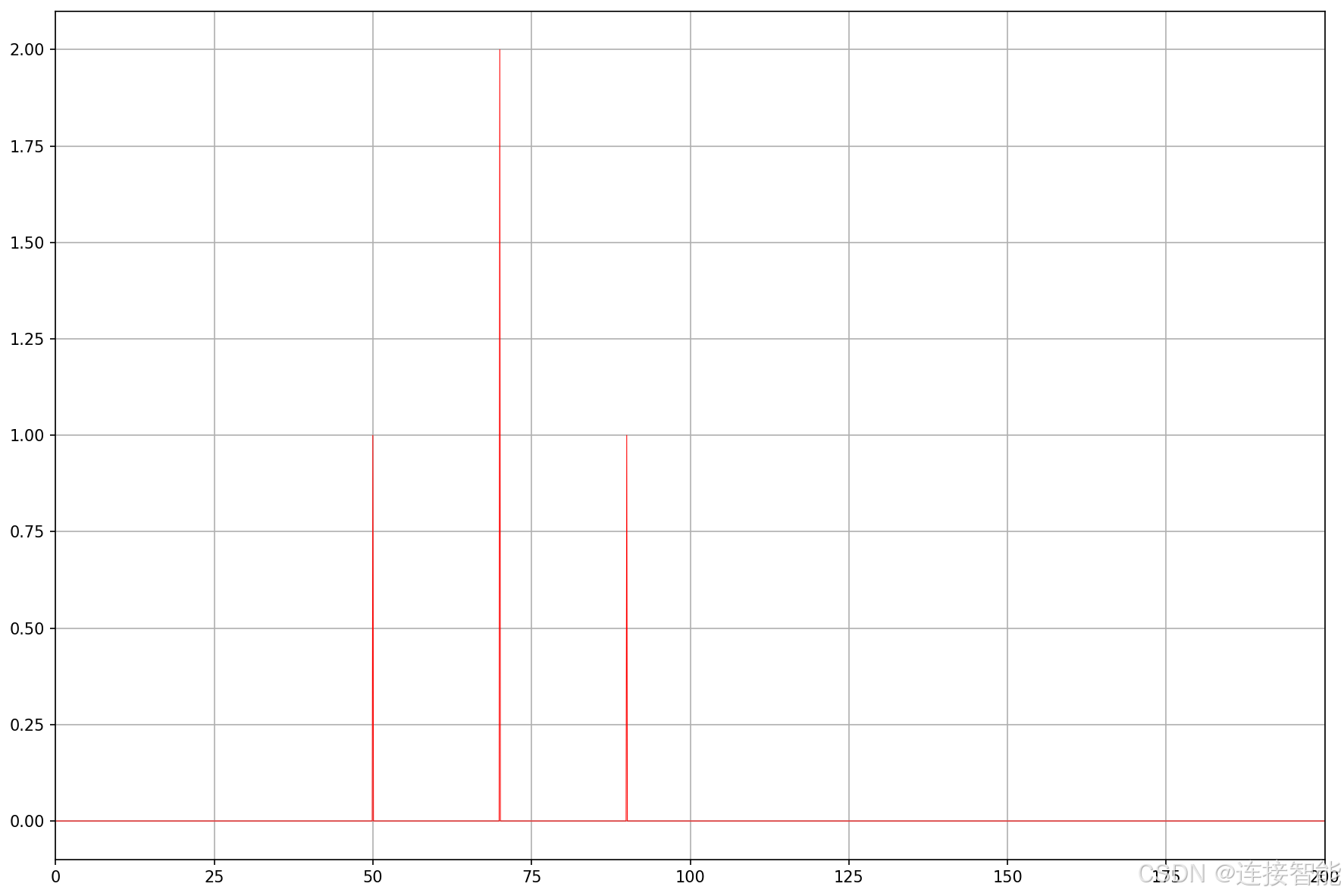
此时可更加清晰地看出，信号是由50Hz、70Hz、90Hz组成，且70Hz的振幅为2，说明FFT分析结果完全正确。

3.3代码说明

代码调用了numpy中的FFT函数实现快速傅里叶变换，然后使用matplotlib包绘制频谱图，整体并不复杂，但有几处关键点需特别注意：

1. np.fft.fft得到的FFT序列中的元素是复数，需要使用np.abs求取振幅值，并且得到的值也并不是真实的振幅，而是需要除以采样点数再乘以2，才能得到真实的振幅值；
2. np.fft.fft得到的FFT序列的索引并不是频率，而是需要将索引除以采样点数再乘以采样频率才能得到频率值，代码中是调用了np.fft.fftfreq函数计算频率值；
3. 由于FFT序列是共轭对称的，因此代码中只截取了FFT序列的一半，因为另一半是对称的，并不影响分析，完整的FFT频谱图如下：
   
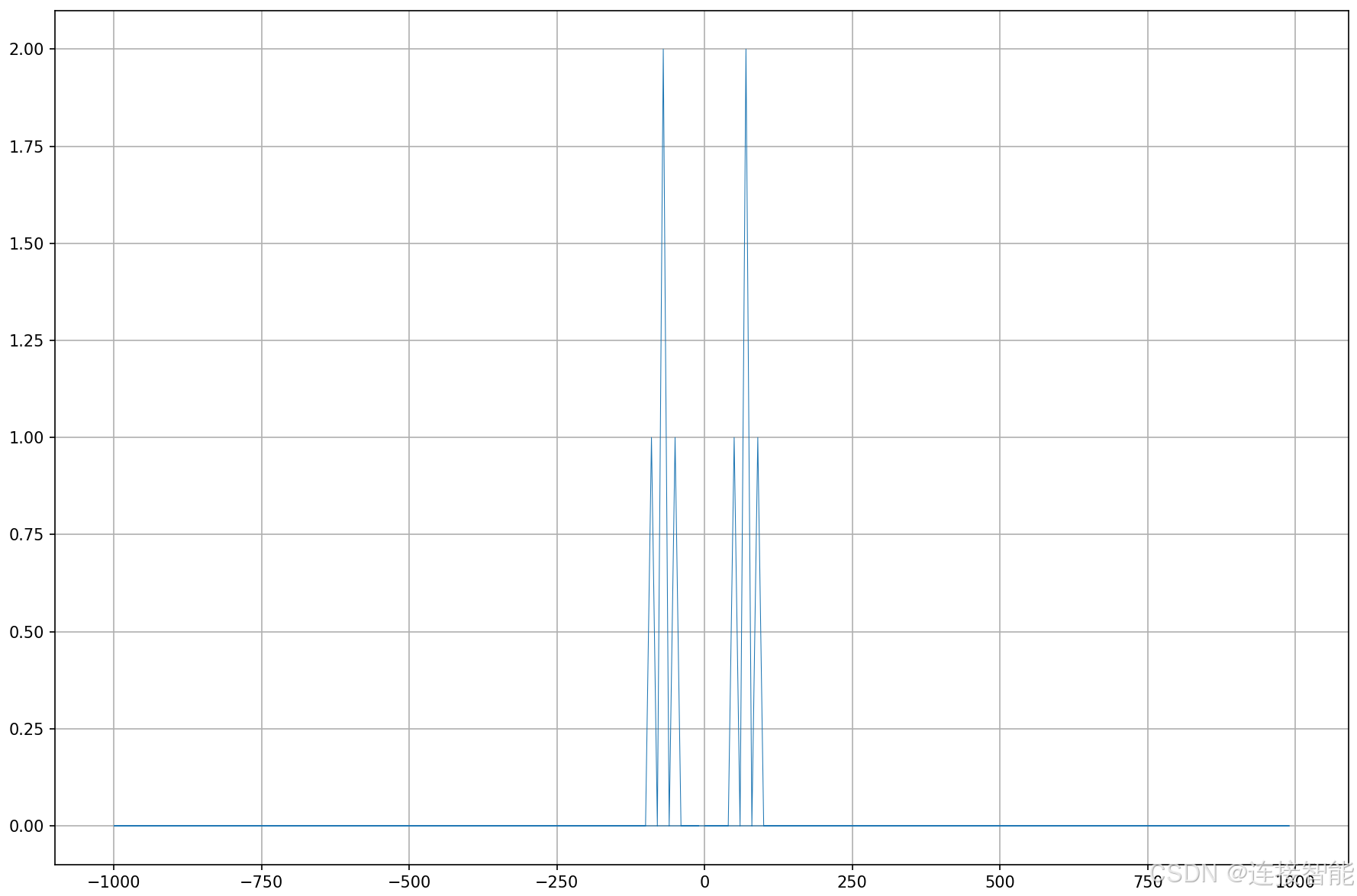
   此外，频谱图中三个频率的形状近似三角形，而不是理论上的脉冲形状，这是由于采样点数较少的缘故。

当将采样时间t设置为1s，采样频率不变，则频谱图如下：

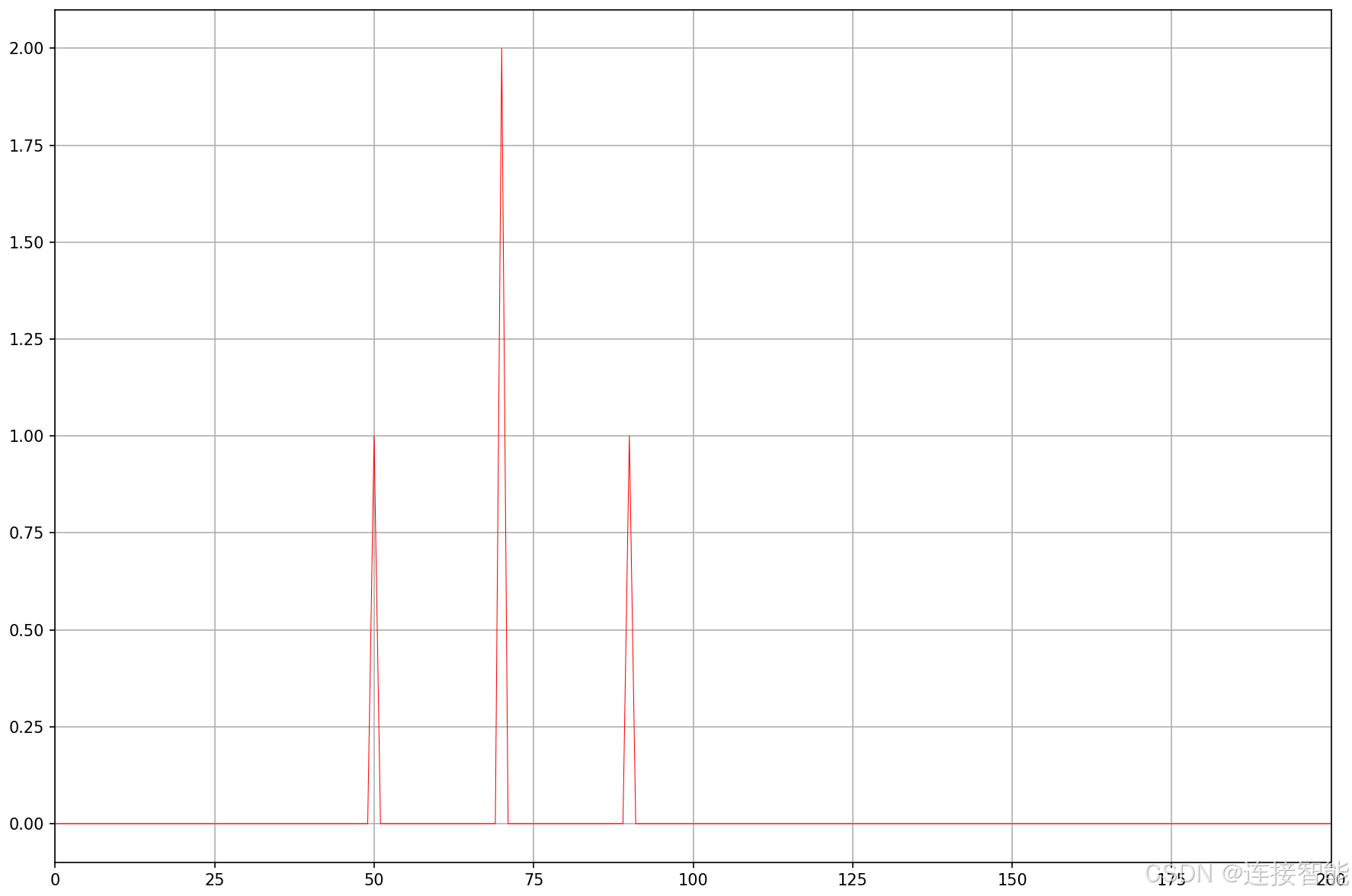
当将采样时间t设置为10s，采样频率不变，频谱图非常接近脉冲的形状：