leetcode 812. 最大三角形面积 简单

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10-5 内的答案将会视为正确答案。

示例 1：

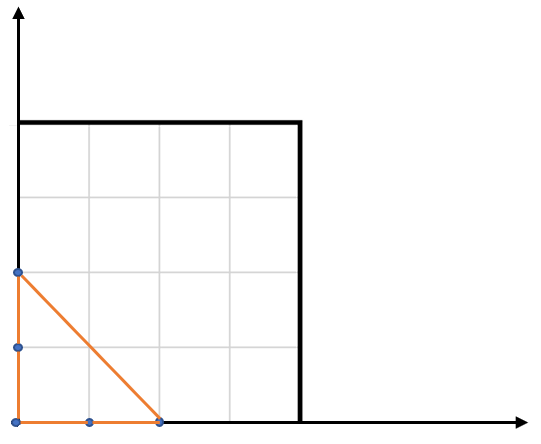
输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出：2.00000
解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入：points = [[1,0],[0,0],[0,1]]
输出：0.50000

提示：

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• 给出的所有点 互不相同

分析：由于点的数量很少，可以直接用三重循环检查所有三个点构成的三角形面积，取最大值作为答案。三角形面积可以用海伦公式求得。

double hellen(double a,double b,double c)
{return sqrt((a+b+c)*(a+b-c)*(a-b+c)*(b+c-a))/4.0;
}
double largestTriangleArea(int** points, int pointsSize, int* pointsColSize) {double ans=0.0;for(int i=0;i<pointsSize-2;++i){for(int j=i+1;j<pointsSize-1;++j){for(int k=j+1;k<pointsSize;++k){double l1,l2,l3;l1=sqrt((points[i][0]-points[j][0])*(points[i][0]-points[j][0])+(points[i][1]-points[j][1])*(points[i][1]-points[j][1]));l2=sqrt((points[i][0]-points[k][0])*(points[i][0]-points[k][0])+(points[i][1]-points[k][1])*(points[i][1]-points[k][1]));l3=sqrt((points[k][0]-points[j][0])*(points[k][0]-points[j][0])+(points[k][1]-points[j][1])*(points[k][1]-points[j][1]));ans=fmax(hellen(l1,l2,l3),ans);}}}return ans;
}