2023 美赛C Predicting Wordle Results(上)
Wordle规则 猜一个五个字母的单词 六次以内机会:
灰色代表正确单词里没有这个字母,黄色代表有这个字母但位置不对,绿色代表位置对。
困难模式:黄色绿色(被猜出来的字母)在下一次猜词中也需要被用到。

后面的题目主要围绕 日期这个时间序列信息,以及词属性特征(衡量难度)。
目录
1. 数据清洗
2. 词特征挖掘
3. 报告数目时间序列预测 Prediction
思路一:SIR传染病模型
思路二:ARIMA + LSTM
4. 困难报告数与词属性关系 Correlation
思路一:多元线性回归
思路二:皮尔逊系数(热力图)
思路三:LightGBM 等集成学习算法
1. 数据清洗
发现 3 个不是5个字母的单词: ['rprobe', 'clen', 'tash']
还有一个拼写错误 marxh -> marsh
import pandas as pd# 读取Excel文件
df = pd.read_excel('Problem_C_Data_Wordle.xlsx', sheet_name='Sheet1')# 首先检查实际的列名
print("数据框的所有列名:")
print(df.columns.tolist())# 检查Word列的单词长度
word_lengths = df['Word'].str.len()print("单词长度统计:")
print(word_lengths.value_counts().sort_index())# 检查是否有不是5个字母的单词
words = df[word_lengths != 5]['Word']
print(f"\n发现 {len(words)} 个不是5个字母的单词:")
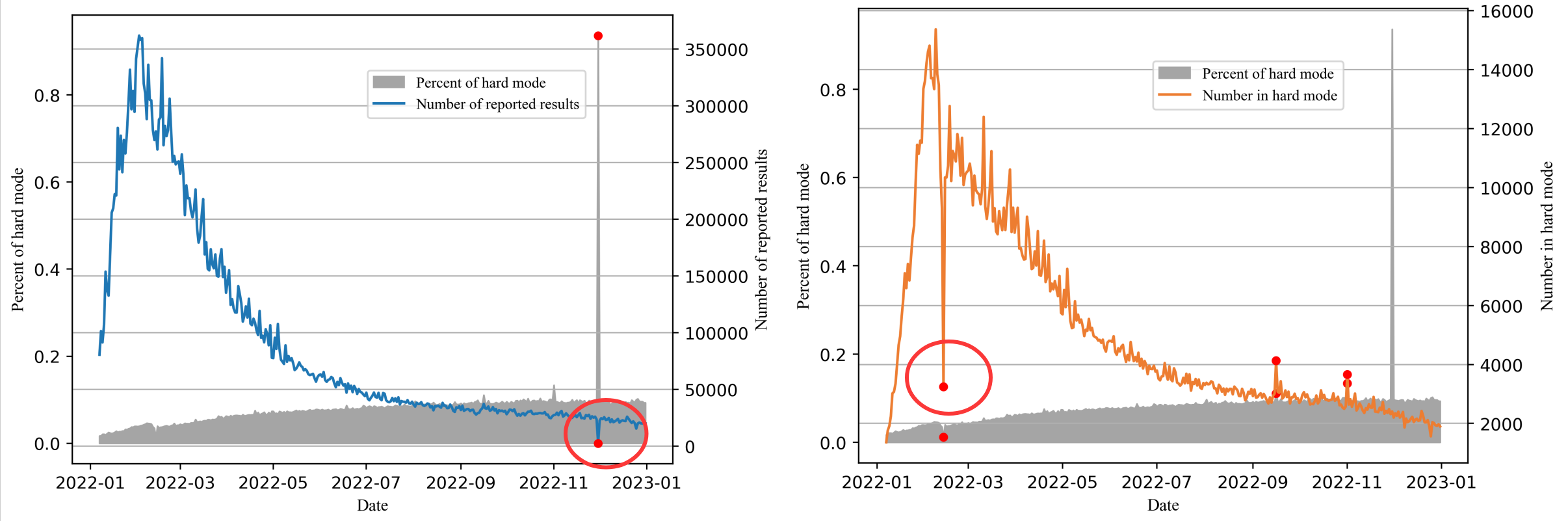
print(words.tolist())可视化两列 report 数目,看outlier 离群值。 下面两个凸出来的点,都理解为少了一位。
Number of reported results 那列的 2022/11/30 2569 -> 25569
Number in hard mode 那列的 2022/2/13 3249 -> 13249
import pandas as pd# 读取Excel文件
df = pd.read_excel('Problem_C_Data_Wordle.xlsx', sheet_name='Sheet1')import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams# 设置中文字体和图形样式
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")for i in (['Number of reported results', 'Number in hard mode']):# 创建图形plt.figure(figsize=(14, 8))# 绘制折线图plt.plot(df['Date'], df[i],linewidth=2, color='#2E86AB', marker='o', markersize=2, alpha=0.7)# 英文标签plt.title(i, fontsize=16, fontweight='bold', pad=20)plt.xlabel('Date', fontsize=12)plt.ylabel(i, fontsize=12)# 优化x轴日期显示plt.xticks(rotation=45)plt.gcf().autofmt_xdate()# 添加网格plt.grid(True, alpha=0.3)plt.legend()plt.tight_layout()plt.show()2. 词特征挖掘
Wordle这个游戏是一个 基于字母猜测的游戏。根据单词内字母的性质。
1. 元音字母(Vowels)“元音字母在单词中出现频率更高”
2. 使用频率(Usage) Python 的 wordfreq库
https://www.kaggle.com/datasets/rtatman/english-word-frequency 或者kaggle的这个数据集
import wordfreq
freq_data = wordfreq.get_frequency_dict('en')freq_data[word] # 即为word的频率3. 每个字母 所有五字母单词中出现的频率 字母频率加和得单词重要程度。
比如由高频字母 a,e,i,o,s,r 组成的单词 raise arose 上来猜一下,得到黄绿块的信息可能比较多。
import wordfreq
import string
from collections import defaultdictvalid_letters = set(string.ascii_lowercase)
def get_letter_freq():# 加载英语单词频率数据(使用"en"表示英语)freq_data = wordfreq.get_frequency_dict('en')freq_words = defaultdict(float)for word, freq in freq_data.items():# 只保留由纯字母组成的5字母单词(排除包含数字、符号的词)if len(word) == 5 and all(c.lower() in valid_letters for c in word):for c in word:freq_words[c] += 1 # 每个字母出现一次# 按频率从高到低排序sorted_freq = sorted(freq_words.items(), key=lambda x: x[1], reverse=True)a = sum(freq for _, freq in sorted_freq)sorted_freq = [(l, freq / a) for l, freq in sorted_freq] # 归一化字母频率return sorted_freqletters = get_letter_freq()# 打印结果
print("字母使用频率:")
for i, (letter, freq) in enumerate(letters, 1):print(f"{i}. {letter} - 频率值: {freq:.6f}")'''
字母使用频率:
1. a - 频率值: 0.124429
2. e - 频率值: 0.092719
3. i - 频率值: 0.071744
4. o - 频率值: 0.069902
5. s - 频率值: 0.066970
6. r - 频率值: 0.062296
'''4. 单词中不同字母的数目(Unique Letters )
5. 单词词性类别 名词,动词,形容词,等等
3. 报告数目时间序列预测 Prediction
在Twitter上晒成绩的数目每天变动,解释这个变动并预测2023.3.1的报告数区间。
思路一:SIR传染病模型
基于经典的SIR传染病模型进行改进,提出了PCQL模型。四类人群&四种系数。
-
变量 P:潜在人群,指那些可能成为成绩上传者,有机会成为跟风者的人。
-
变量 C:跟风人群,指普通的成绩上传者,他们会很快感到厌倦;其中一部分人每天会变成退出者或忠诚者。
-
变量 Q:退出人群,指那些对游戏或上传成绩感到厌倦的人。
-
变量 L:忠诚人群,指那些不会轻易放弃成绩分享行为的人。
-
参数 β:潜在->跟风比率。
-
参数 γ:跟风者退出比率。
-
参数 λ:跟风者转变为忠诚者的可能性。
-
参数 φ:忠诚者退出比率。

C+L为对应晒成绩的人数,使用遗传算法得到参数的初始比较好的参数解。
再使用 Nelder-Mead方法(下山单纯形法)像更好的方向微调。
预测与区间估计:为了给出预测值及其不确定性(预测区间),使用了Bootstrap方法。
-
过程:生成大量(1000个)Bootstrap数据样本。对每个样本重复步骤2的拟合过程,并预测2023年3月1日的数值。这样就得到了1000个预测值,形成了一个预测分布。
-
结果:计算这1000个预测值的平均值作为点预测(14689.9)。取这个预测分布的2.5% 和97.5% 分位数,作为95%置信水平下的预测区间([11173.04, 17069.15])。
思路二:ARIMA + LSTM
ADF检验是否平稳,进行一阶差分发现 2022年5月16日前后方差变化很大。为了保证序列的稳定性(恒定方差),只使用了该日期之后的数据作为最终建模的时间序列。
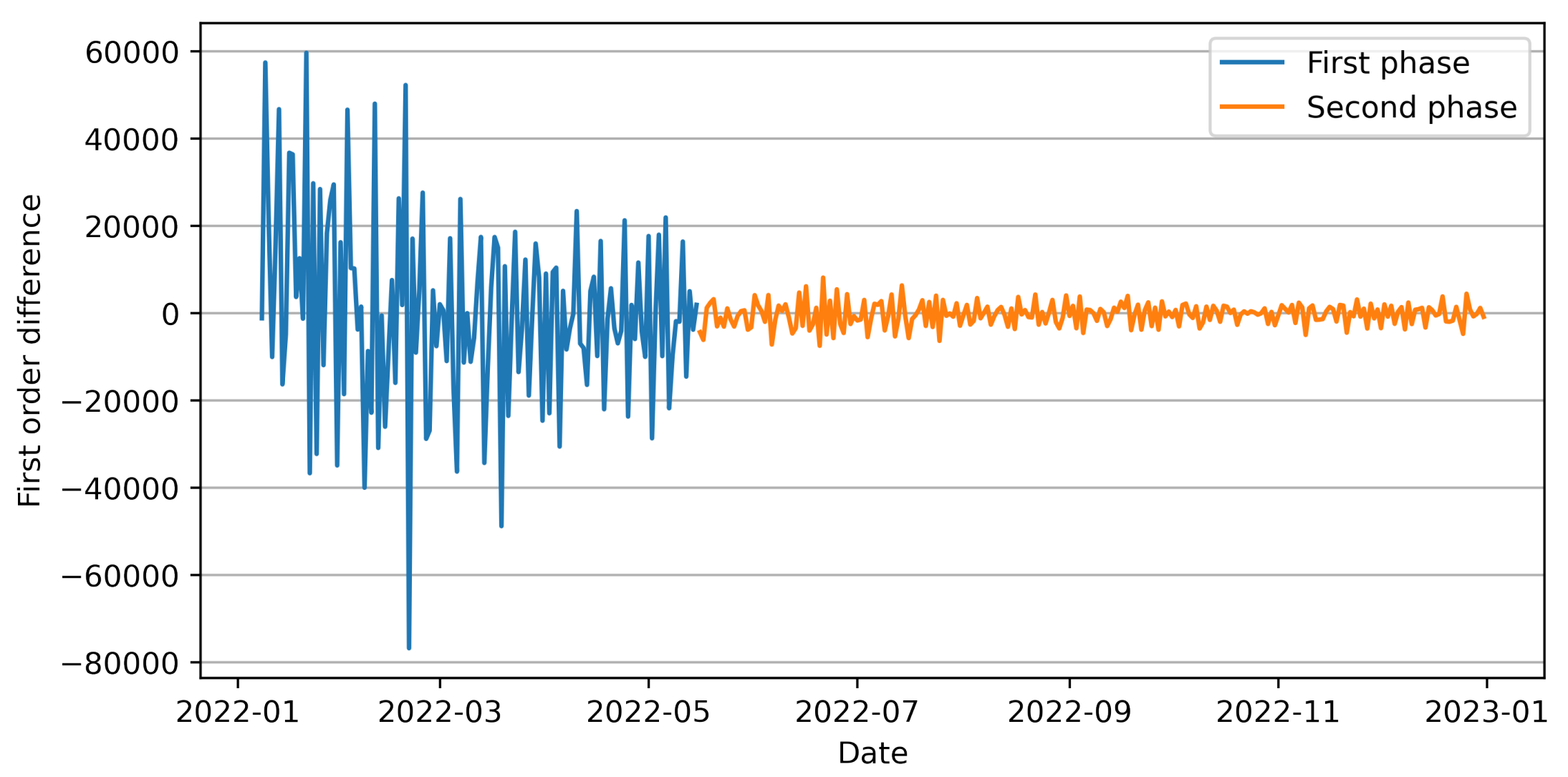
后面一段进行ADF检验。
# 后一段的 ADF 检验
from statsmodels.tsa.stattools import adfuller# 提取从第 131 个数据往后的数据
data_subset = df['report_reversed_diff1'][130:]# 进行 ADF 检验
result = adfuller(data_subset.dropna())# 输出 ADF 检验结果
print('ADF 统计量:', result[0])
print('p 值:', result[1])
print('临界值:')
for key, value in result[4].items():print(f' {key}: {value}')对平稳序列定阶 (ACF/PACF图 + AIC准则) -> 模型诊断 (残差白噪声检验 如Ljung-Box检验)
AIC(赤池信息量准则) AIC = 2k - 2ln(L)
| 模型类型 | AR(p) 自回归模型 | MA(q) 移动平均模型 | ARMA(p,q) 混合模型 |
|---|---|---|---|
| ACF | 拖尾 | 在滞后q阶后截尾 | 拖尾 |
| PACF | 在滞后p阶后截尾 | 拖尾 | 拖尾 |
如果用差分后的 (0,0,1) 会导致后面的预测期望和区间都恒定不变,转回差分前(0,1,1)
模型训练 + Ljung - Box 检验 (残差应近似白噪声)
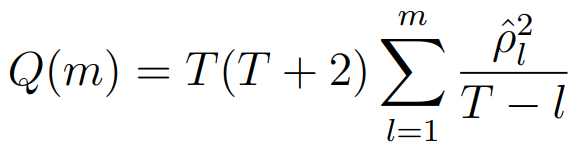
import statsmodels.api as sm
from statsmodels.stats.diagnostic import acorr_ljungbox# 按照 (0, 1, 1) 拟合 ARIMA 模型
data_subset = df['report_reversed'][130:]
model = sm.tsa.ARIMA(data_subset, order=(0, 1, 1))
results = model.fit()# 获取模型残差
residuals = results.resid# 进行 Ljung - Box 检验,这里检验前 10 个滞后期
lb_test = acorr_ljungbox(residuals, lags=10)print('Ljung - Box 检验结果:')
print(lb_test)往后预测60个日期 期望和区间(但是效果并不好范围很大 下限都到负数了,原论文数据造假嫌疑)
# 进行向后 60 步的预测
forecast = results.get_forecast(steps=60)# 获取点预测值
point_forecast = forecast.predicted_mean# 获取 95% 置信区间预测
confidence_interval = forecast.conf_int()print('向后 60 步的点预测值:')
print(point_forecast)
print('\n向后 60 步的 95% 置信区间预测:')
print(confidence_interval)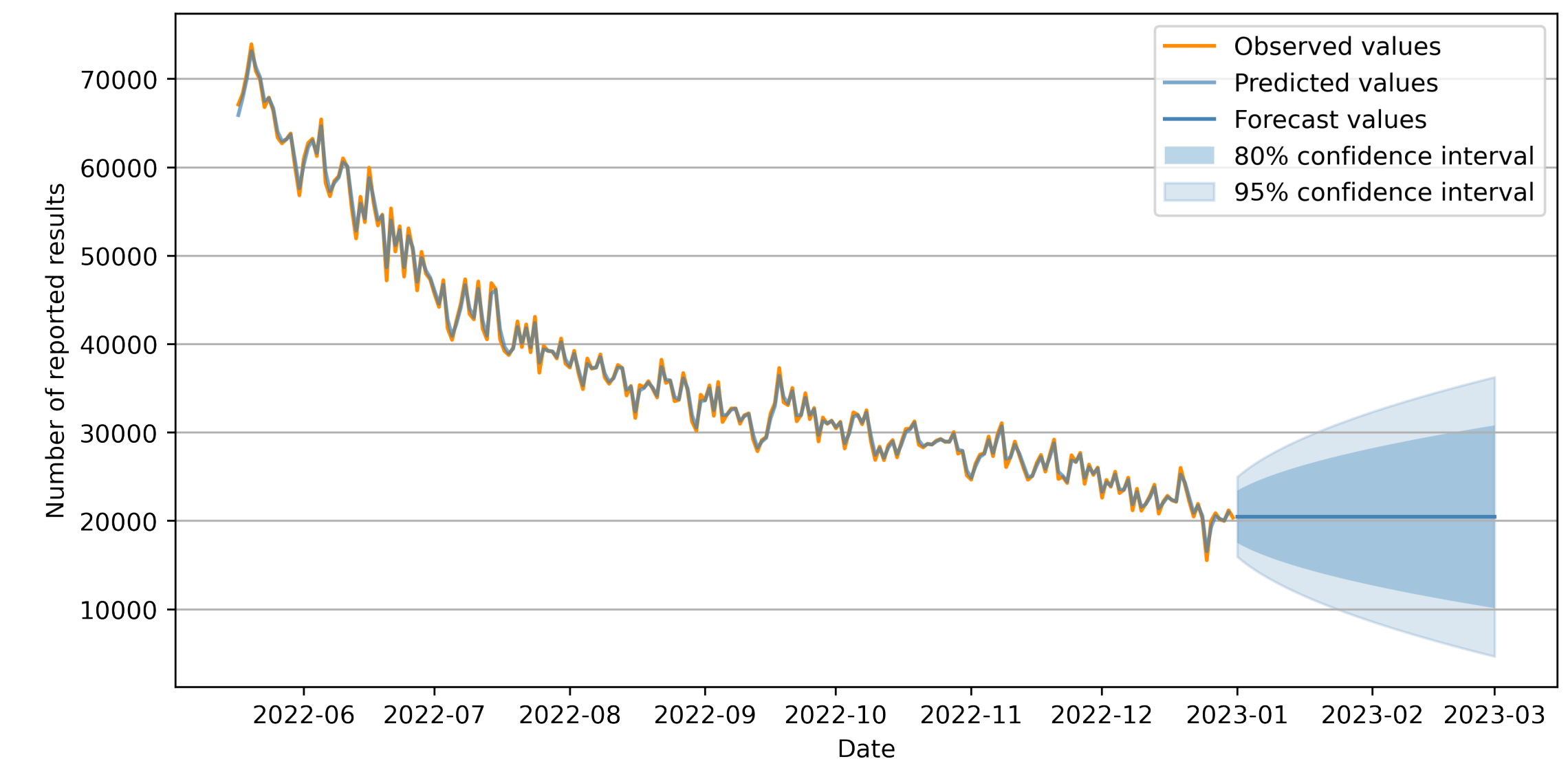
但是 ARIMA(0,1,1) 数学逻辑决定了它只能捕捉数据的线性趋势与短期随机波动,无法处理非线性特征。超过 1 步后,未来的白噪声 无法预测,最佳估计为其均值 0;所以导致后面的期望是一条直线定值。
由于 ARIMA 模型的预测结果波动性较差(其预测结果的残差部分未能得到合理预测),将 ARIMA 与 LSTM 相结合。
- 基于 ARIMA 的预测结果与实际报告数量,计算出 “报告数量残差序列”(残差 = 实际值 - ARIMA 预测值),并将该残差序列作为 LSTM 神经网络的期望输出(即 LSTM 需学习预测的目标);
- 对原始数据进行 “相空间重构”(一种将一维时间序列转化为高维空间向量,以挖掘数据时序特征的方法),最终确定最优重构维度为 18,作为 LSTM 的输入数据;
- 将训练集输入 LSTM 神经网络,对残差序列的测试集进行学习建模与预测,得到 ARIMA 残差序列的预测值;
- 最后,将 ARIMA 模型的预测结果与 LSTM 模型的残差预测结果相加,得到报告数量的最终预测结果。
4. 困难报告数与词属性关系 Correlation
词的属性是否与 玩困难模式的报告比例ratio 相关。是的话,什么属性?不是的话,为什么。
思路一:多元线性回归
F统计量 衡量模型所解释的方差与未被解释的方差的比率。
F = (模型解释的方差 / 模型的自由度) / (残差的方差 / 残差的自由度)
t 统计量 单个特征的影响程度。 但这篇论文给出的是不相关。
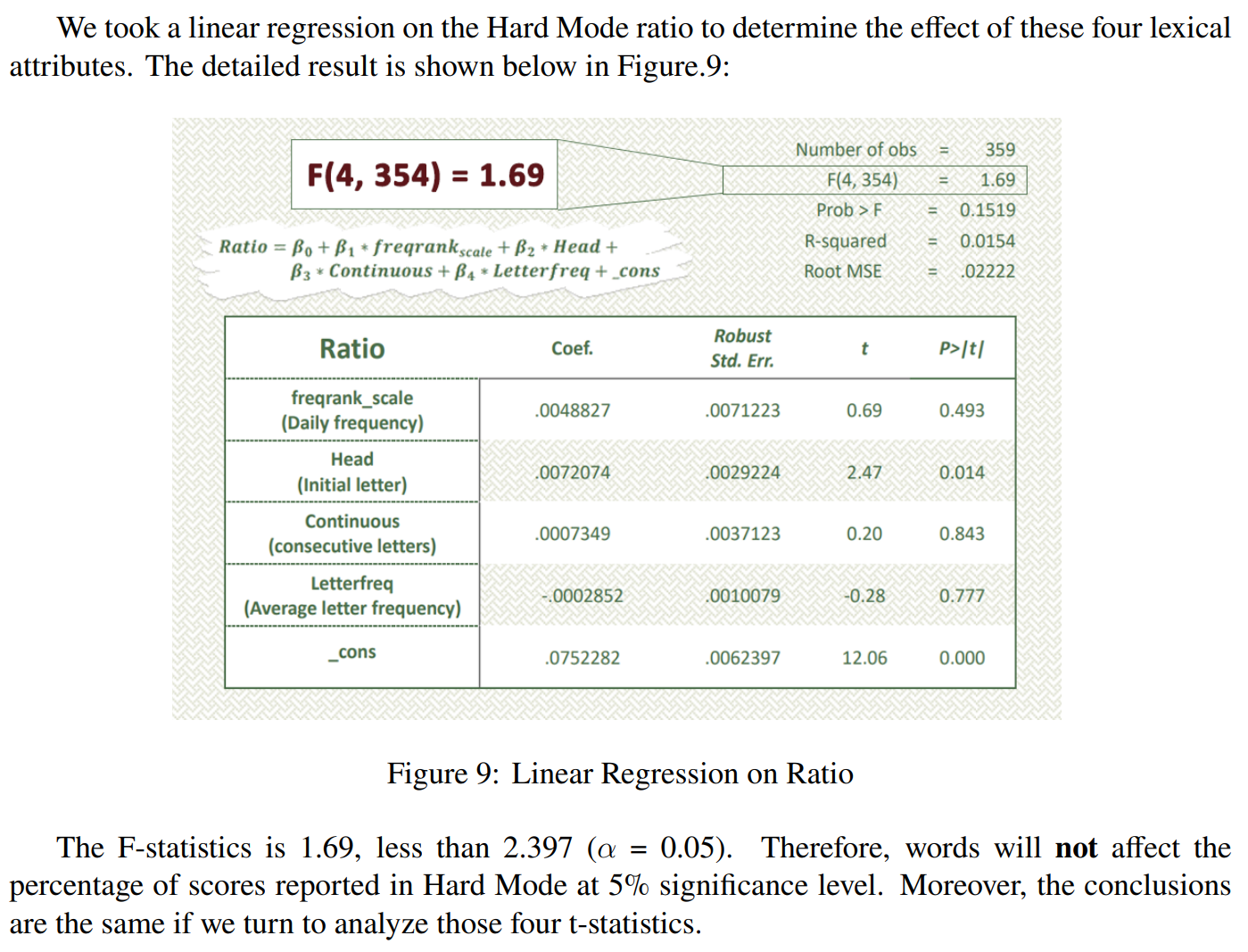
思路二:皮尔逊系数(热力图)
import pandas as pdcorrelation_matrix = df.corr(method='pearson')import matplotlib.pyplot as plt
import seaborn as snsplt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix,annot=True, # 在单元格内显示数值cmap='coolwarm', # 使用一个从蓝色(负)到红色(正)的配色center=0, # 中心点为 0square=True, # 让单元格为正方形fmt=’.2f’) # 数值保留两位小数
plt.title('Pearson Correlation Heatmap')
plt.show()思路三:LightGBM 等集成学习算法
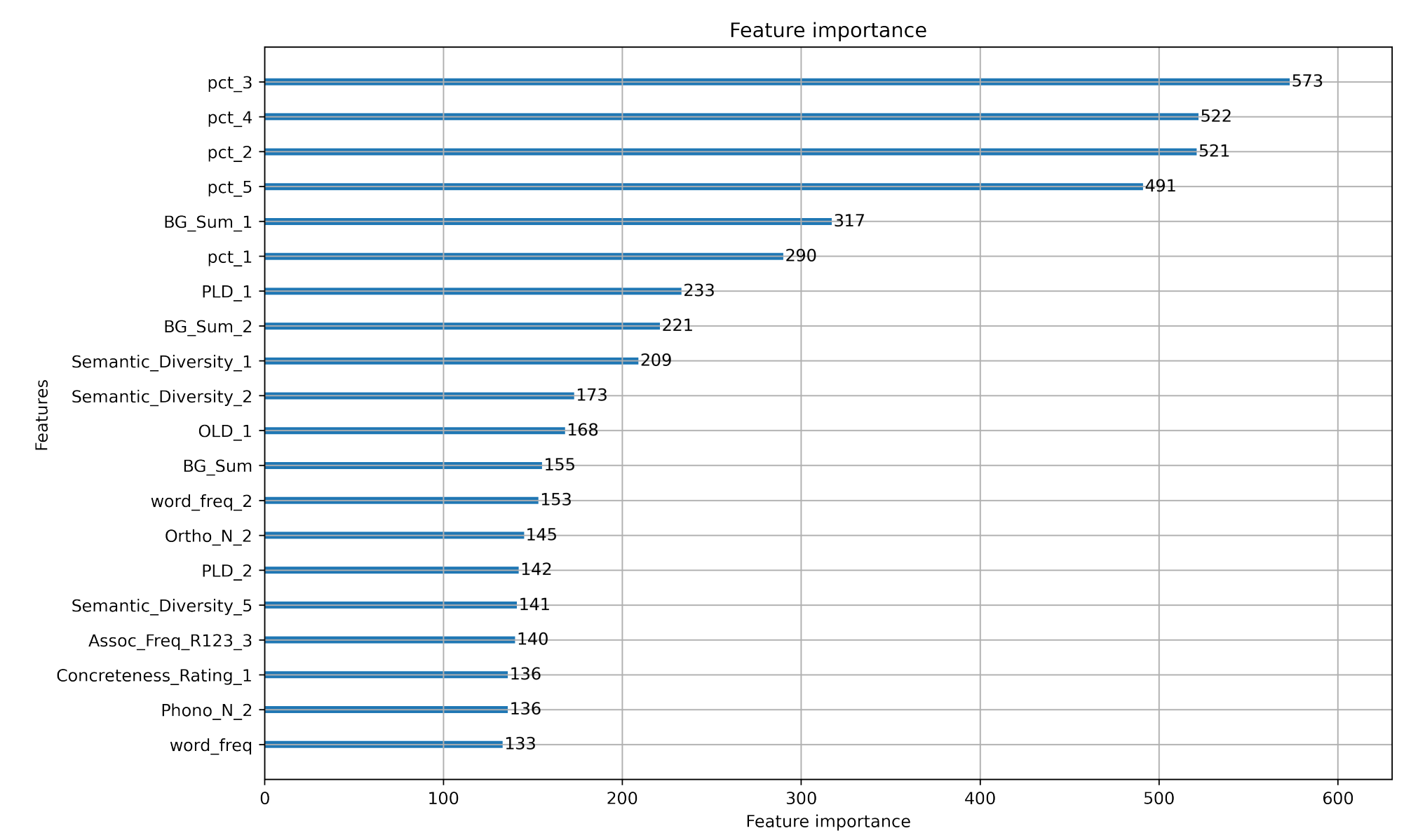
得到每个特征权重;但需要多选几个特征,不然可能过拟合。