动态规划实战
目录
一、不同的二叉搜索树(LeetCode 96):卡特兰数与DP的碰撞
二、组合总和 IV(LeetCode 377):排列型背包问题
三、盈利计划(LeetCode 879):多维背包的复杂DP
四、一和零(LeetCode 474):二维背包的最大值问题
五、完全平方数(LeetCode 279):完全背包的最小数问题
总结:动态规划的解题方法论
动态规划(Dynamic Programming,简称DP)是算法领域中解决多阶段决策问题的利器。它通过将复杂问题分解为重叠子问题,并存储子问题的解以避免重复计算,从而高效地解决问题。本文将结合几道LeetCode经典题目,深入剖析动态规划的解题思路、状态定义与转移方程的推导过程。
一、不同的二叉搜索树(LeetCode 96):卡特兰数与DP的碰撞
题目分析
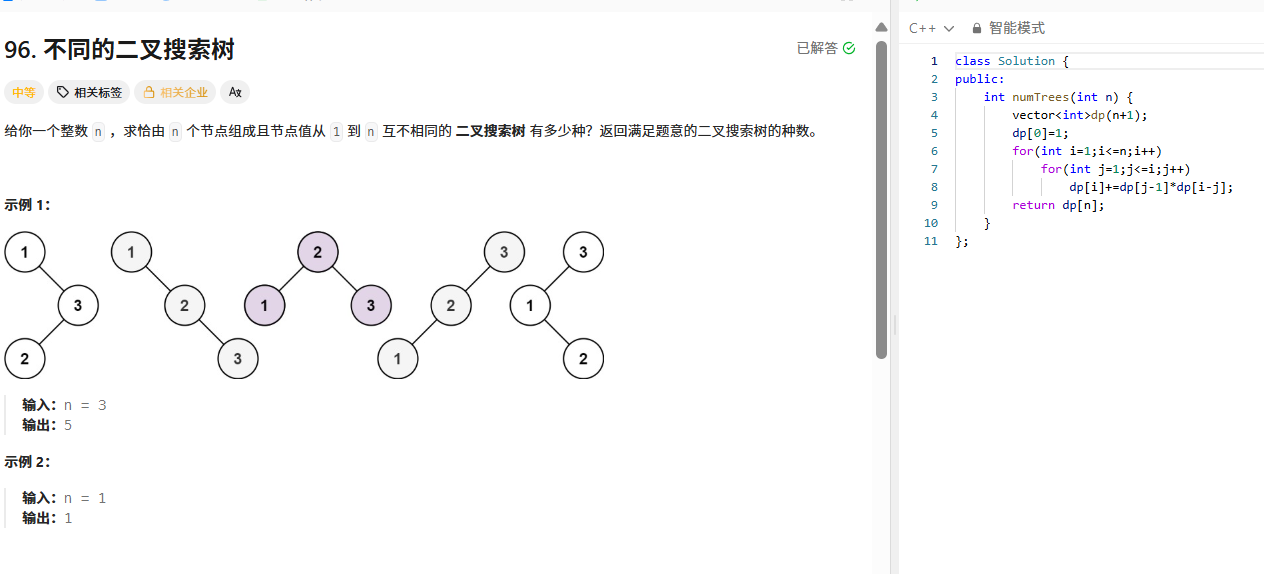
给定整数 n ,求由 1~n 组成的不同二叉搜索树的种数。二叉搜索树的性质是:左子树所有节点值小于根节点,右子树所有节点值大于根节点。
状态定义与转移
- 状态定义: dp[i] 表示 i 个节点能组成的不同二叉搜索树的种数。
- 转移方程:对于 i 个节点,选择 j 作为根节点( 1≤j≤i ),则左子树有 j-1 个节点,右子树有 i-j 个节点,因此 dp[i] += dp[j-1] * dp[i-j] 。
- 初始条件: dp[0] = 1 (空树也算一种情况,用于递归基础)。
代码与理解
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= i; ++j) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};
这道题的本质是卡特兰数的应用,动态规划通过枚举根节点的位置,将问题分解为左右子树的子问题,完美体现了“重叠子问题”与“最优子结构”的DP核心思想。
二、组合总和 IV(LeetCode 377):排列型背包问题
题目分析
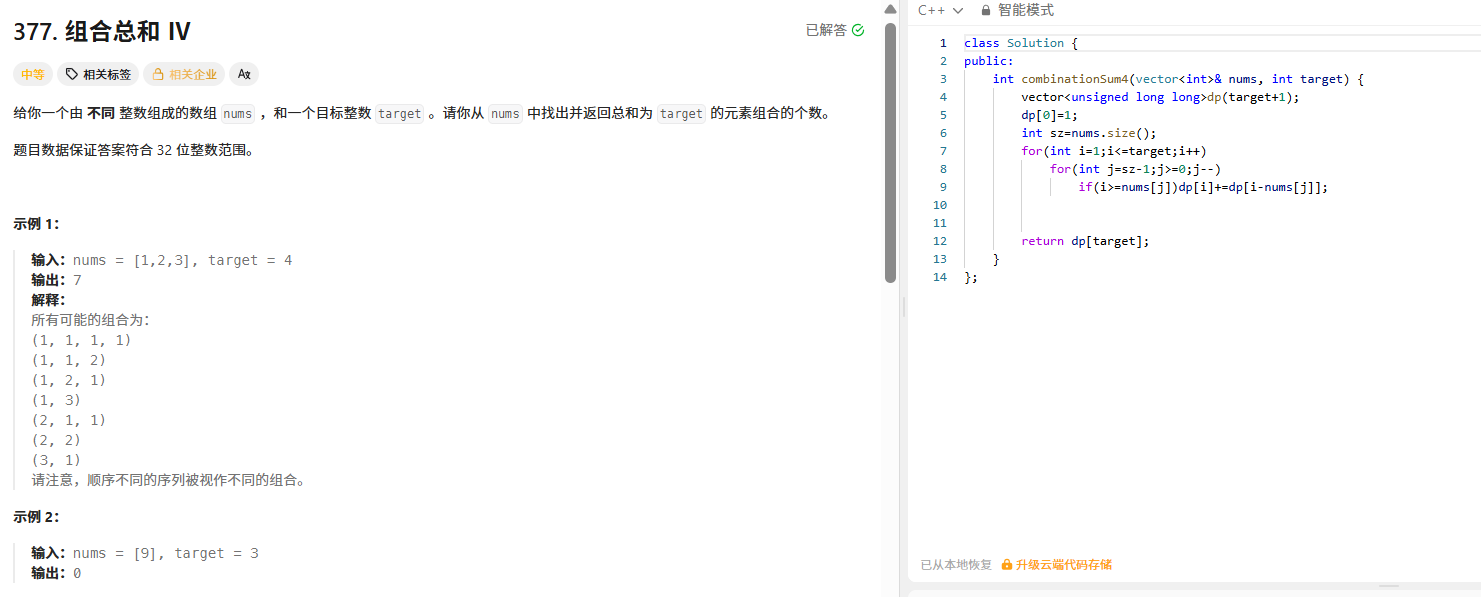
给定不同整数的数组 nums 和目标值 target ,求元素和为 target 的排列个数(顺序不同视为不同组合)。
状态定义与转移
- 状态定义: dp[i] 表示和为 i 的组合排列个数。
- 转移方程:对于每个 i ,遍历 nums 中的元素 num ,若 i ≥ num ,则 dp[i] += dp[i - num] 。
- 遍历顺序:由于是“排列”(顺序敏感),需先遍历目标和,再遍历物品,确保每个元素能以不同顺序被多次选择。
代码与理解
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<unsigned long long> dp(target + 1);dp[0] = 1;int sz = nums.size();for (int i = 1; i <= target; ++i) {for (int j = sz - 1; j >= 0; --j) { // 此处正序、逆序不影响(因nums元素可重复选,且是排列)if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};
这道题是完全背包问题的变种,区别在于“排列”与“组合”的遍历顺序差异。若为组合(顺序不敏感),需先遍历物品再遍历目标和;若为排列(顺序敏感),则先遍历目标和再遍历物品。
三、盈利计划(LeetCode 879):多维背包的复杂DP
题目分析
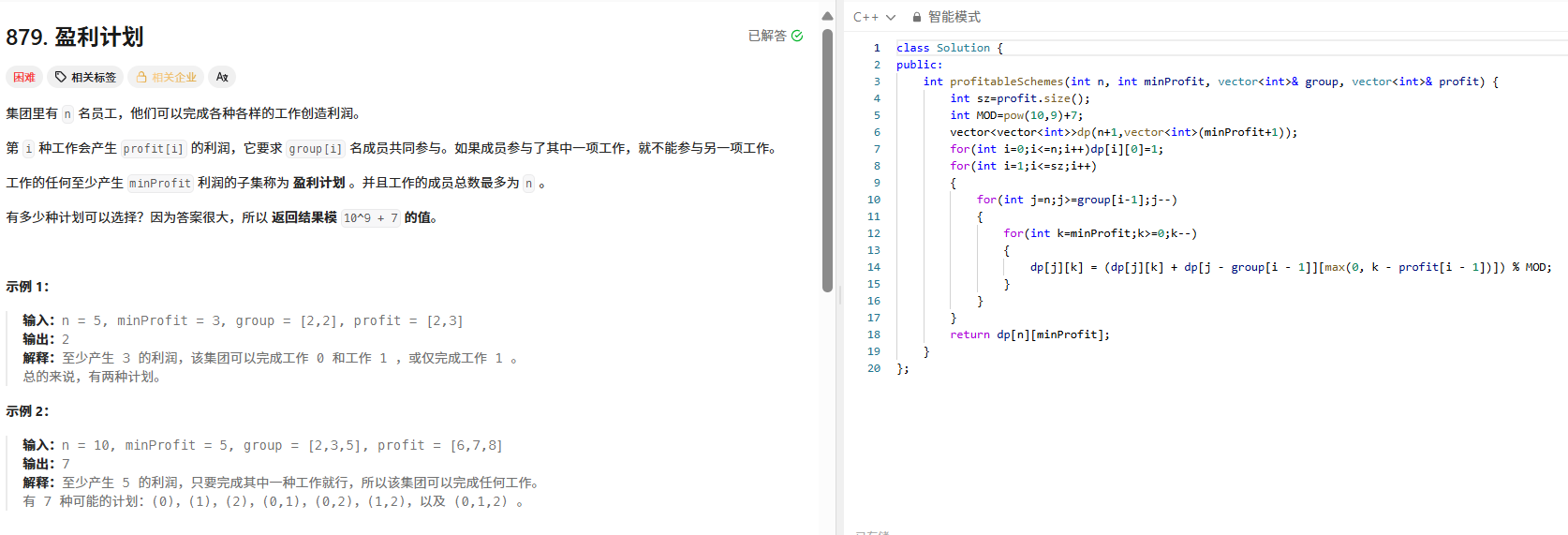
有 n 名员工,多项工作(每项工作需 group[i] 人,产生 profit[i] 利润)。求员工总数不超过 n 且利润至少为 minProfit 的“盈利计划”种数。
状态定义与转移
- 状态定义: dp[j][k] 表示用 j 名员工,获得 k 利润的计划数。
- 转移方程:对于第 i 项工作,若选择执行,则 dp[j][k] += dp[j - group[i-1]][max(0, k - profit[i-1])] (利润超过 minProfit 时,统一记为 minProfit 以减少状态数)。
- 初始条件: dp[0][0] = 1 (0人0利润是一种基础情况)。
代码与理解
class Solution {
public:int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {int sz = profit.size();int MOD = 1e9 + 7;vector<vector<int>> dp(n + 1, vector<int>(minProfit + 1));for (int i = 0; i <= n; ++i) dp[i][0] = 1; // 利润为0的情况初始化为1for (int i = 1; i <= sz; ++i) {int g = group[i - 1], p = profit[i - 1];for (int j = n; j >= g; --j) { // 员工数逆序(01背包)for (int k = minProfit; k >= 0; --k) {dp[j][k] = (dp[j][k] + dp[j - g][max(0, k - p)]) % MOD;}}}return dp[n][minProfit];}
};
这道题是三维DP压缩为二维的典型案例,通过“员工数”和“利润”两个维度,结合01背包的逆序遍历技巧,解决了多约束下的计数问题。
四、一和零(LeetCode 474):二维背包的最大值问题
题目分析
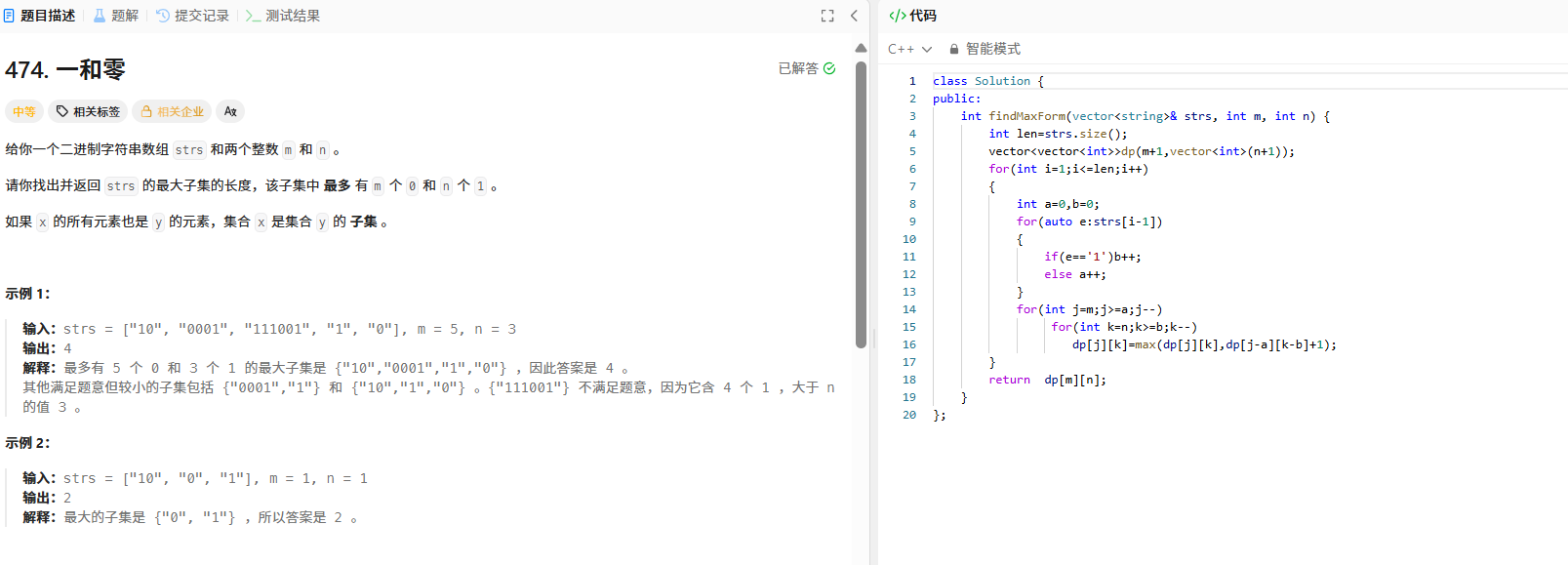
给定二进制字符串数组 strs ,以及最大0的数量 m 和最大1的数量 n ,求满足条件的最大子集长度。
状态定义与转移
- 状态定义: dp[j][k] 表示用 j 个0和 k 个1能组成的最大子集长度。
- 转移方程:对于每个字符串,统计其0的数量 a 和1的数量 b ,则 dp[j][k] = max(dp[j][k[j dp[j - a][k - b] + 1) (若 j≥a 且 k≥b )。
- 遍历顺序:逆序遍历 j 和 k (避免物品重复选择,属于01背包逻辑)。
代码与理解
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {int len = strs.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for (int i = 1; i <= len; ++i) {int a = 0, b = 0;for (auto c : strs[i - 1]) {if (c == '1') b++;else a++;}for (int j = m; j >= a; --j) {for (int k = n; k >= b; --k) {dp[j][k] = max(dp[j][k[j dp[j - a][k - b] + 1);}}}return dp[m][n];}
};
这道题是二维01背包问题,将“0的数量”和“1的数量”作为两个背包容量,目标是最大化子集长度,充分体现了DP在多约束优化问题中的灵活性。
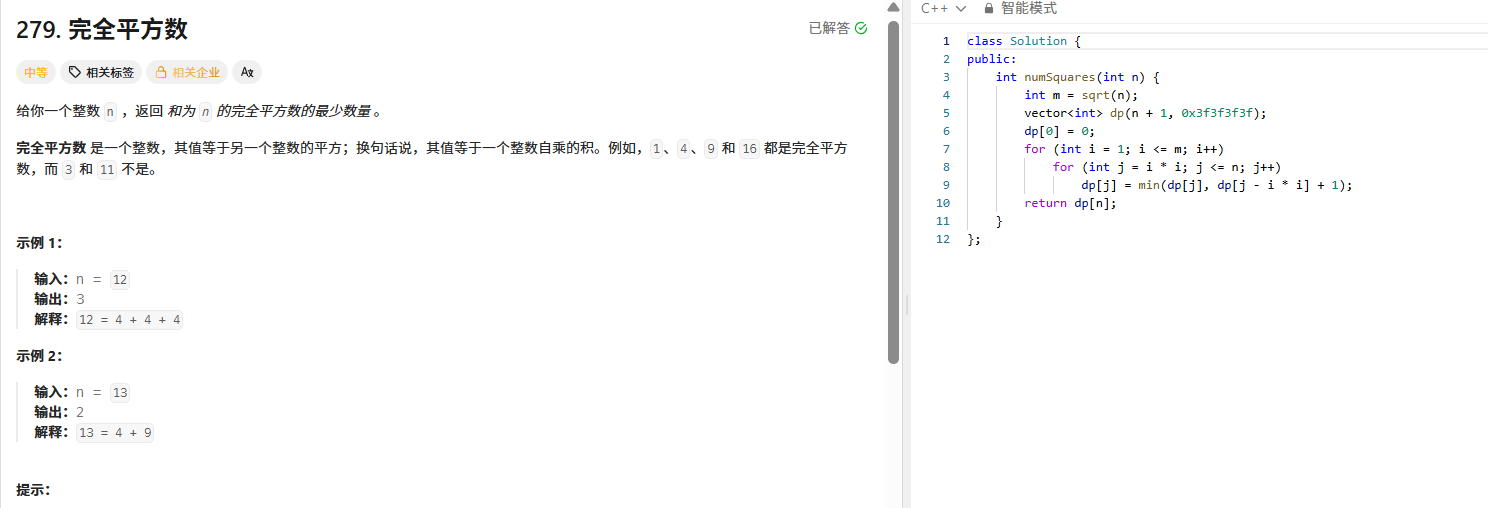
五、完全平方数(LeetCode 279):完全背包的最小数问题
题目分析
给定整数 n ,求组成 n 的最少完全平方数个数(如 12=4+4+4 ,输出3)。
状态定义与转移
- 状态定义: dp[i] 表示和为 i 的最少完全平方数个数。
- 转移方程:对于每个完全平方数 j² ( j≤√i ), dp[i] = min(dp[i], dp[i - j²] + 1) 。
- 初始条件: dp[0] = 0 ,其余初始化为一个很大的数(表示不可达)。
代码与理解
class Solution {
public:int numSquares(int n) {int m = sqrt(n);vector<int> dp(n + 1, 0x3f3f3f3f);dp[0] = 0;for (int i = 1; i <= m; ++i) {int square = i * i;for (int j = square; j <= n; ++j) { // 完全背包,正序遍历dp[j] = min(dp[j[j dp[j - square] + 1);}}return dp[n];}
};
这道题是完全背包的最小值问题,完全平方数可重复选择(如 4 可多次选),因此采用正序遍历物品的方式,最终得到最少数量。
总结:动态规划的解题方法论
通过以上五道题,我们可以总结出动态规划的通用解题步骤:
1. 明确状态定义:找到问题的“可变维度”,定义 dp 数组的含义(如“数量”“最大值”“最小值”等)。
2. 推导转移方程:分析“选择”对状态的影响,将当前状态分解为子问题的状态。
3. 确定遍历顺序:根据“物品是否可重复选”“是排列还是组合”等条件,选择正序或逆序遍历。
4. 处理初始条件:确保递归/递推的基础情况正确,避免数组越界或逻辑错误。
动态规划的核心是“状态的抽象与转移的逻辑”,掌握这两点,再结合背包问题、计数问题、最值问题等经典模型的思路,就能在复杂问题中举一反三,高效解决各类DP题目。
