烟台 网站建设中国广告在国外投放案例
题目链接:73. 矩阵置零 - 力扣(LeetCode)
题目描述
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用原地算法。
示例 1:
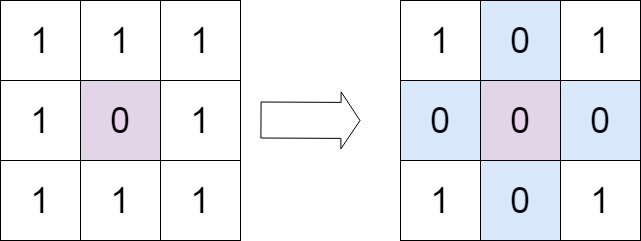
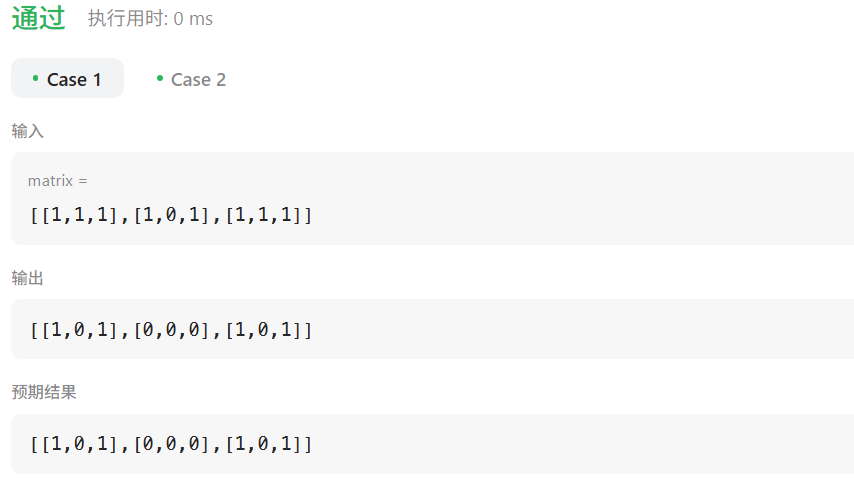
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
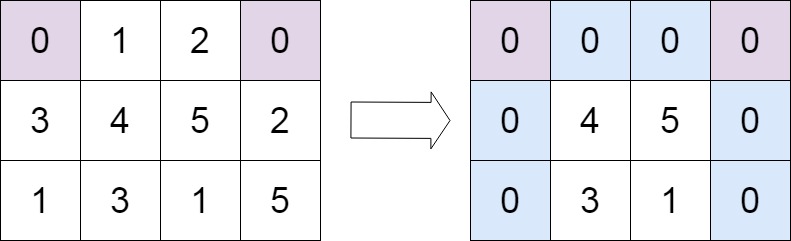
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
-
m == matrix.length -
n == matrix[0].length -
1 <= m, n <= 200 -
-231 <= matrix[i][j] <= 231 - 1
题目作答
解决这个问题的关键在于,我们需要一个地方来记录哪些行和哪些列需要被置为零,但又不能使用与矩阵大小成正比的额外空间(比如创建两个数组来分别记录行和列)。
一个朴素的方法是创建一个 O(m+n) 空间的布尔数组来记录,但这不满足“原地”算法的要求。
所以,最高效的原地算法思想是:利用矩阵自身的第一行和第一列作为标记空间。再额外添加一个空间来记录第一列本身是否需要被置零。
这个思想可以分解为以下步骤:
-
处理第一行和第一列的特殊性:第一行和第一列既是普通的矩阵行列,又即将被我们用作“标记行”和“标记列”。 matrix[0][0] 这个元素尤其特殊,它同时位于标记行和标记列的交点上。为了避免信息混淆,我们需要一个独立的变量来专门记录第一列本身是否需要被置零。而第一行是否需要置零的信息,我们可以安全地存储在 matrix[0][0] 中。
-
标记:
-
首先,我们先扫描第一列,如果其中有0,就将 flag_col0 设为 true。
-
然后,我们从第二列开始,扫描整个矩阵(除了第一列)。如果发现 matrix[i][j] 为0,我们就将这个信息标记在第一行和第一列上,即令 matrix[i][0] = 0 和 matrix[0][j] = 0。
-
-
置零:
-
根据刚才设置的标记,我们再次遍历矩阵(同样从第二行第二列开始)。如果 matrix[i][j] 对应的标记位 matrix[i][0] 或 matrix[0][j] 为0,就将 matrix[i][j] 置为0。
-
这一步完成后,除了第一行和第一列之外的矩阵部分就已经更新完毕。
-
-
处理第一行和第一列:
-
这是最后一步,必须在其他所有元素都处理完之后进行,否则会过早地破坏我们的标记。
-
首先检查 matrix[0][0]。如果它为0,说明第一行需要被置零,我们就将第一行所有元素设为0。
-
然后检查我们最初的标志位 flag_col0。如果它为 true,我们就将第一列所有元素设为0。
-
通过这个流程,我们只使用了一个额外的布尔变量,空间复杂度为 O(1),并且通过设计后的顺序完成了原地修改。
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {if (matrix.empty()) {return;}int m = matrix.size();int n = matrix[0].size();// 使用一个布尔变量记录第一列是否需要置零bool flag_col0 = false;for (int i = 0; i < m; i++) {if (matrix[i][0] == 0) {flag_col0 = true;break;}}// 检查第一行是否需要置零(除了 matrix[0][0])// 并用第一行和第一列记录其他行列是否需要置零for (int i = 0; i < m; i++) {// 从第二列开始检查for (int j = 1; j < n; j++) {if (matrix[i][j] == 0) {// 标记在第一行和第一列matrix[i][0] = 0;matrix[0][j] = 0;}}}// 根据标记,将非首行首列的元素置零// 从第二行第二列开始for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}// 最后处理第一行和第一列// 必须放在最后,否则会破坏标记// 首先检查 matrix[0][0],它记录了第一行是否需要置零// 这个检查必须在处理第一列之前,因为第一列的处理可能会修改 matrix[0][0]if (matrix[0][0] == 0) {for (int j = 0; j < n; j++) {matrix[0][j] = 0;}}// 根据 flag_col0 决定是否将第一列置零if (flag_col0) {for (int i = 0; i < m; i++) {matrix[i][0] = 0;}}}
};