当前位置：首页 > news >正文

Leetcode+Java+单调栈

news 2025/9/30 8:38:59

注：单调栈在以下题目并不是最优方法，最优是双指针

739.每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示：
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100

原理

初始化一个空栈，存储天数的索引。
遍历温度数组 temperatures：
如果栈不为空且当前温度 temperatures[i] 大于栈顶索引对应的温度：
弹出栈顶索引 index，计算 answer[index] = i - index（当前天与栈顶天的差值）。
重复此过程，直到栈为空或当前温度不再大于栈顶温度。
将当前天的索引 i 压入栈。
遍历结束后，栈中剩余的索引对应的天没有更高的温度，answer 中对应位置默认为 0。

代码

import java.util.*;class Solution {public int[] dailyTemperatures(int[] temperatures) {int len = temperatures.length;// 初始化结果数组 answer，长度与输入数组相同，默认值为 0int[] answer = new int[len];// 创建一个栈，存储天数的索引，维护单调递减的温度序列Stack<Integer> stack = new Stack<>();// 将第一天的索引压入栈，作为起点stack.push(0);// 从第二天（索引 1）开始遍历for (int i = 1; i < len; i++) {// 当栈不为空且当前温度大于栈顶索引对应的温度while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {// 获取栈顶索引（即等待找到更高温度的天）int index = stack.peek();// 计算当前天 i 与栈顶天 index 的差值，存入 answeranswer[index] = i - stack.pop();}// 将当前天的索引 i 压入栈，等待后续更高温度stack.push(i);}// 返回结果数组，栈中剩余的索引对应的 answer 值为 0（默认值）return answer;}
}

496.下一个更大元素I

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置右侧的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1：
输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
示例 2：
输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。
提示：
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 104
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中

原理

问题本质：
给定两个数组 nums1 和 nums2，nums1 是 nums2 的子集（无重复元素）。
对于 nums1[i]，找到它在 nums2 中的对应位置 j（即 nums1[i] == nums2[j]），然后在 nums2 中寻找从 j 向右的第一个比 nums2[j] 大的元素，返回该元素的值。如果不存在，则返回 -1。
结果存储在数组 ans 中，ans[i] 表示 nums1[i] 的下一个更大元素。
单调栈的核心思想：
使用一个栈维护一个单调递减的元素序列（存储 nums2 中的元素值）。
遍历 nums2 时：
如果当前元素 nums2[i] 大于栈顶元素，则栈顶元素找到“下一个更大元素”，记录结果并弹出栈顶。
将当前元素压入栈，继续维护单调性。
遍历结束后，栈中剩余的元素没有下一个更大元素，记录为 -1。
最后，根据 nums1 的元素查询结果。
为什么用单调栈？
单调栈适合解决“下一个更大元素”问题，因为它能高效地跟踪尚未找到更大元素的元素。
时间复杂度为 O(n)，其中 n 是 nums2 的长度；空间复杂度为 O(n)，用于栈和存储结果。
算法步骤：
初始化一个栈和一个映射（或数组）来存储每个元素的下一个更大元素。
遍历 nums2：
如果栈不为空且当前元素 nums2[i] 大于栈顶元素：
弹出栈顶元素，记录 nums2[i] 为其下一个更大元素。
将当前元素压入栈。
栈中剩余的元素没有下一个更大元素，记录为 -1。
根据 nums1 的元素，从映射中提取结果。

代码

import java.util.*;class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {// 初始化结果数组，长度为 nums1.lengthint[] result = new int[nums1.length];// 使用 HashMap 存储 nums2 中每个元素的下一个更大元素Map<Integer, Integer> nextGreater = new HashMap<>();// 创建单调栈，存储 nums2 的元素值Stack<Integer> stack = new Stack<>();// 遍历 nums2，寻找每个元素的下一个更大元素for (int num : nums2) {// 当栈不为空且当前元素大于栈顶元素while (!stack.isEmpty() && num > stack.peek()) {// 弹出栈顶元素，记录 num 为其下一个更大元素nextGreater.put(stack.pop(), num);}// 将当前元素压入栈stack.push(num);}// 栈中剩余的元素没有下一个更大元素，设为 -1while (!stack.isEmpty()) {nextGreater.put(stack.pop(), -1);}// 根据 nums1 的元素，从 nextGreater 中提取结果for (int i = 0; i < nums1.length; i++) {result[i] = nextGreater.get(nums1[i]);}return result;}
}

503.下一个更大元素II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。
示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
提示:
1 <= nums.length <= 104
-109 <= nums[i] <= 109

原理

问题本质：
给定一个循环数组 nums，对于每个元素 nums[i]，需要找到从位置 i 开始（向右循环，包括回到数组开头）的第一个比 nums[i] 大的元素。
如果不存在更大的元素，则返回 -1。
循环数组意味着 nums[nums.length - 1] 的下一个元素是 nums[0]。
单调栈的核心思想：
使用一个栈维护一个单调递减的元素序列（存储数组索引）。
由于是循环数组，需要模拟遍历两倍数组长度（2 * len），以确保每个元素都能检查到循环后的元素。
遍历时：
如果当前元素 nums[i % len] 大于栈顶索引对应的元素，则栈顶元素找到“下一个更大元素”，记录结果并弹出栈顶。
将当前索引压入栈，继续维护单调性。
栈中剩余的元素（在两次遍历后）没有更大的元素，answer 数组对应位置保持为 -1。
为什么用单调栈？
单调栈适合解决“下一个更大元素”问题，因为它能高效跟踪尚未找到更大元素的索引。
循环数组的处理通过遍历两倍长度（2 * len）实现，模拟从数组末尾回到开头。
时间复杂度为 O(n)，每个元素最多被压栈和弹栈一次；空间复杂度为 O(n)，用于栈和结果数组。
算法步骤：
初始化结果数组 answer，默认值为 -1。
创建一个单调栈，存储数组索引。
遍历数组两遍（0 到 2 * len - 1）：
使用 i % len 获取循环数组的索引。
如果当前元素大于栈顶索引对应的元素，弹出栈顶并记录结果。
将当前索引压入栈。
返回结果数组。

代码

import java.util.*;class Solution {public int[] nextGreaterElements(int[] nums) {int len = nums.length;// 初始化结果数组，长度为 nums.length，默认值为 -1int[] answer = new int[len];Arrays.fill(answer, -1);// 使用 ArrayDeque 作为栈，存储索引，维护单调递减序列Deque<Integer> stack = new ArrayDeque<>();// 遍历 2*len 次，模拟循环数组（从头到尾再回到头）for (int i = 0; i < 2 * len; i++) {// 使用 i % len 获取循环数组的索引int currIndex = i % len;// 当栈不为空且当前元素大于栈顶索引对应的元素while (!stack.isEmpty() && nums[currIndex] > nums[stack.peek()]) {// 弹出栈顶索引，将当前元素值赋给 answeranswer[stack.pop()] = nums[currIndex];}// 将当前索引压入栈，等待寻找下一个更大元素stack.push(currIndex);}// 返回结果数组，栈中剩余的索引对应的 answer 值为 -1（默认值）return answer;}
}

42.接雨水

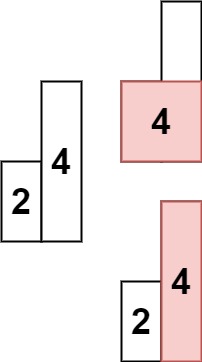
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 
示例 2：
输入：height = [4,2,0,3,2,5]
输出：9
提示：
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

原理

问题本质：
给定一个数组 height，每个元素表示宽度为 1 的柱子高度，计算这些柱子形成的凹槽能接多少雨水。
雨水能被接住的条件是：某个位置 i 的左右两侧存在比 height[i] 高的柱子，形成一个凹槽，雨水量由最低的左右柱子高度决定。
雨水量计算公式为：min(左边高度, 右边高度) - 当前高度 × 宽度。
单调栈的核心思想：
使用一个单调递减的栈，存储柱子的索引，栈中对应的柱子高度从栈底到栈顶递减。
遍历数组时：
如果当前柱子高度 height[index] 小于栈顶柱子高度，压入栈（表示当前柱子可能形成凹槽）。
如果当前柱子高度等于栈顶高度，弹出栈顶并压入当前索引（因为相邻相等高度的柱子，左侧的无法接水）。
如果当前柱子高度大于栈顶高度，弹出栈顶，计算凹槽的雨水量（基于栈顶和栈顶前一个柱子），重复直到栈顶高度大于等于当前高度。
将当前索引压入栈。
栈维护了潜在的凹槽边界，弹出时计算雨水量。
为什么用单调栈？
单调栈适合处理“寻找左右两侧更高元素”的问题，能高效找到每个凹槽的左右边界。
通过栈的弹出操作，动态维护凹槽的边界，计算雨水量。
时间复杂度为 O(n)，每个索引最多被压栈和弹栈一次；空间复杂度为 O(n)，用于栈。
算法步骤：
初始化一个空栈，存储柱子索引。
遍历数组 height：
如果当前柱子高度小于栈顶高度，压入栈。
如果当前柱子高度等于栈顶高度，替换栈顶索引。
如果当前柱子高度大于栈顶高度：
弹出栈顶（中间柱子），用栈顶前一个柱子（左边界）和当前柱子（右边界）计算雨水量。
雨水量 = min(左边界高度, 右边界高度) - 中间柱子高度 × 宽度。
重复直到栈为空或栈顶高度大于等于当前高度。
压入当前索引。
返回总雨水量。

代码

class Solution {public int trap(int[] height) {int size = height.length;// 如果数组长度 <= 2，无法形成凹槽，直接返回 0if (size <= 2) return 0;// 初始化单调栈，存储柱子索引，维护递减高度序列Stack<Integer> stack = new Stack<>();// 将第一个柱子索引压入栈stack.push(0);int sum = 0; // 累计雨水量// 遍历数组，从第二个柱子开始for (int index = 1; index < size; index++) {int stackTop = stack.peek(); // 获取栈顶索引if (height[index] < height[stackTop]) {// 当前柱子高度小于栈顶，压入栈，可能形成凹槽stack.push(index);} else if (height[index] == height[stackTop]) {// 当前柱子高度等于栈顶，弹出栈顶（左侧相等柱子无法接水），压入当前索引stack.pop();stack.push(index);} else {// 当前柱子高度大于栈顶，计算凹槽的雨水量int heightAtIdx = height[index]; // 当前柱子高度while (!stack.isEmpty() && heightAtIdx > height[stackTop]) {// 弹出栈顶（中间柱子）int mid = stack.pop();if (!stack.isEmpty()) {// 获取左边界（栈顶前一个柱子）int left = stack.peek();// 雨水高度 = min(左边界高度, 右边界高度) - 中间柱子高度int h = Math.min(height[left], height[index]) - height[mid];// 雨水宽度 = 右边界索引 - 左边界索引 - 1int w = index - left - 1;// 计算雨水量并累加int hold = h * w;if (hold > 0) sum += hold;// 更新栈顶索引，继续检查stackTop = stack.peek();}}// 当前索引压入栈，等待后续处理stack.push(index);}}return sum; // 返回总雨水量}
}

84.柱状图中最大的矩形

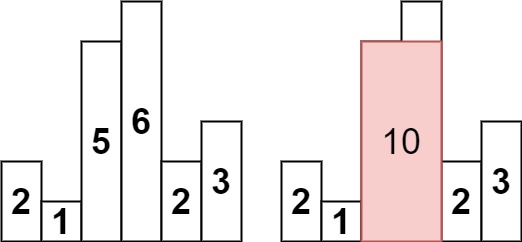
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
示例 1:
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10
示例 2：
输入： heights = [2,4]
输出： 4
提示：
1 <= heights.length <=105
0 <= heights[i] <= 104

原理

问题本质：
给定一个非负整数数组 heights，每个元素表示宽度为 1 的柱子高度，求由这些柱子形成的矩形的最大面积。
矩形面积由宽度（连续柱子的数量）和高度（最低柱子的高度）决定。
对于每个柱子，最大矩形面积可能是以该柱子高度为高的矩形，宽度由左右第一个比它矮的柱子决定。
单调栈的核心思想：
使用一个单调递增的栈，存储柱子索引，栈中对应的柱子高度从栈底到栈顶递增。
遍历数组时：
如果当前柱子高度 heights[i] 大于或等于栈顶柱子高度，压入栈（表示当前柱子可能参与更大的矩形）。
如果当前柱子高度小于栈顶柱子高度，弹出栈顶，计算以栈顶柱子高度为高的矩形面积：
宽度：当前索引 i（右边界）与栈顶前一个索引（左边界）之间的距离。
高度：栈顶柱子的高度。
重复弹出直到栈顶高度小于或等于当前高度，然后压入当前索引。
为了简化边界处理，在数组两端添加高度为 0 的“哨兵”柱子，确保所有柱子都能被弹出并计算面积。
为什么用单调栈？
单调栈适合解决“寻找左右两侧第一个更小元素”的问题，能高效确定每个柱子作为高度时的最大宽度。
栈维护了尚未找到右边界的柱子，弹出时计算面积。
时间复杂度为 O(n)，每个索引最多被压栈和弹栈一次；空间复杂度为 O(n)，用于栈和扩展数组。
算法步骤：
创建新数组 newHeight，在原数组 heights 两端添加高度 0（哨兵）。
初始化一个单调递增栈，存储索引，压入第一个索引（0）。
遍历 newHeight：
如果当前高度小于栈顶高度，弹出栈顶，计算面积：
宽度：当前索引 - 栈顶前一个索引 - 1。
高度：栈顶柱子的高度。
更新最大面积。
压入当前索引。
返回最大面积。

代码

class Solution {public int largestRectangleArea(int[] heights) {// 创建新数组，两端添加高度 0（哨兵），简化边界处理int[] newHeight = new int[heights.length + 2];System.arraycopy(heights, 0, newHeight, 1, heights.length);newHeight[heights.length + 1] = 0;newHeight[0] = 0;// 初始化单调递增栈，存储索引，维护递增高度序列Stack<Integer> stack = new Stack<>();stack.push(0); // 压入第一个哨兵索引int res = 0; // 记录最大矩形面积// 遍历新数组for (int i = 1; i < newHeight.length; i++) {// 当当前柱子高度小于栈顶高度，计算栈顶柱子的矩形面积while (newHeight[i] < newHeight[stack.peek()]) {int mid = stack.pop(); // 弹出栈顶索引（当前计算的柱子）int w = i - stack.peek() - 1; // 宽度 = 当前索引 - 左边界索引 - 1int h = newHeight[mid]; // 高度 = 栈顶柱子的高度res = Math.max(res, w * h); // 更新最大面积}stack.push(i); // 当前索引压入栈}return res; // 返回最大面积}
}

查看全文

http://www.dtcms.com/a/423109.html