现代控制理论4——第3章线性控制系统的能控性和能观性（1）

 摘要：本文主要内容为现代控制理论第3章线性控制系统的能控性和能观性的前半部分内容。

声明：本文章内容整理于浙江大学王建全副教授的MOOC课程《现代控制理论》，仅作个人学习使用，若有侵权，请联系删除。

文章阅读推荐顺序：

1、现代控制理论1——第1章控制系统的状态空间表达式（1）

2、现代控制理论2——第1章控制系统的状态空间表达式（2）

3、现代控制理论3——第2章控制系统状态空间表达式的解

4、本文

---

​

---

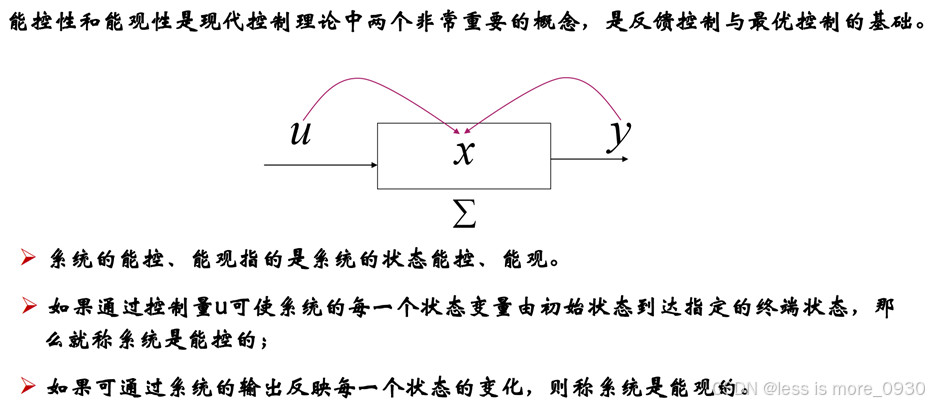
1.1 线性定常系统的能控性

1.1.1 定义

1.1.2 能控性Gram矩阵判据

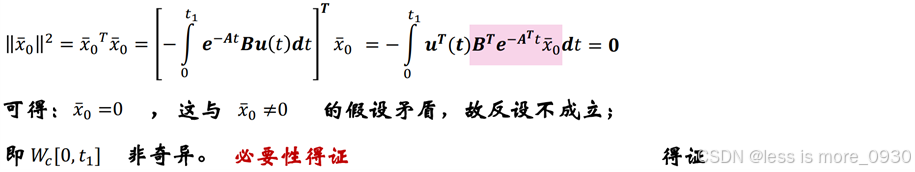
       Gram矩阵判据是依据系统能控性的矩阵推导出来的，具有重要理论意义。但是利用Gram矩阵判据需要计算系统的转移矩阵，需要积分，需要计算行列式的值，计算量较大，因此还需要研究即便的计算方法用于判断系统的能控性。

1.1.3 能控性秩判据

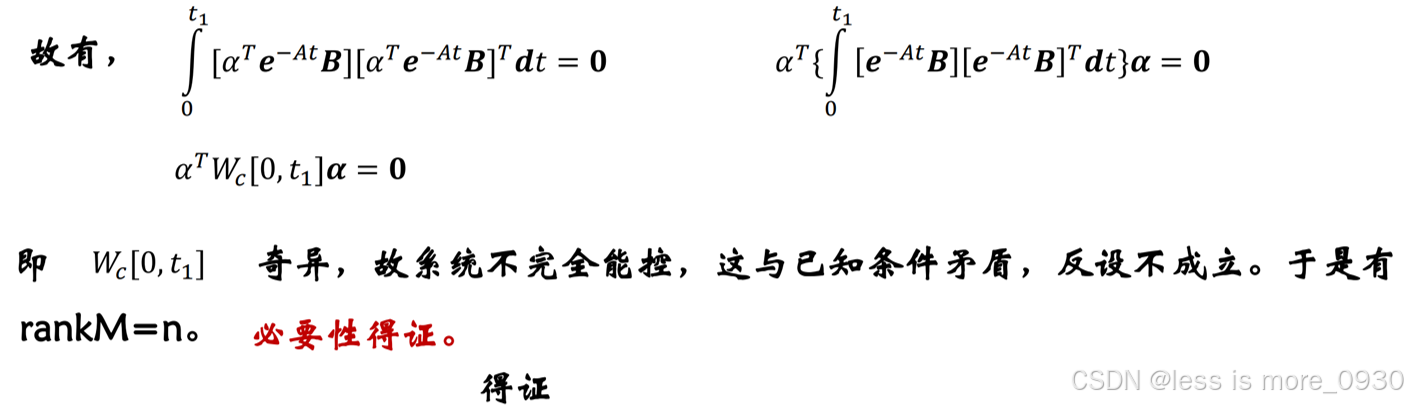
       秩判据只能给出整个系统是否能控的结论，对于不完全能控的系统，哪些特征根可移动，哪些特征根不可移动，秩判据不能给出具体的信息。

1.1.4 能控性PBH判据

       PBH判据要计算每一个特征值的能控性自判别矩阵，计算量比秩矩阵判据大。

       λ2这个特征根不可控，不能通过状态反馈控制来移动极点λ2。

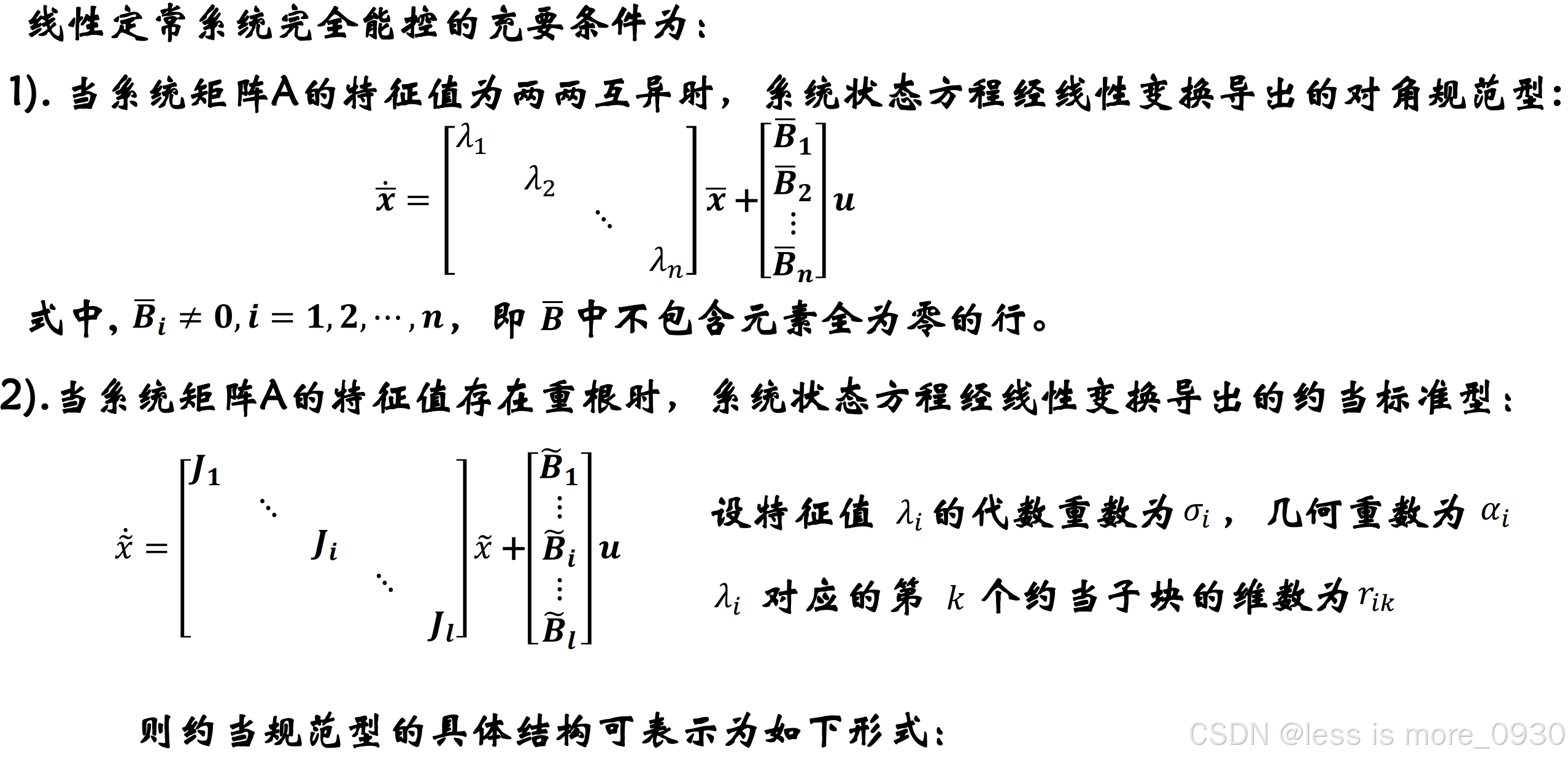
 1.1.5 能控性规范型判据

    

---

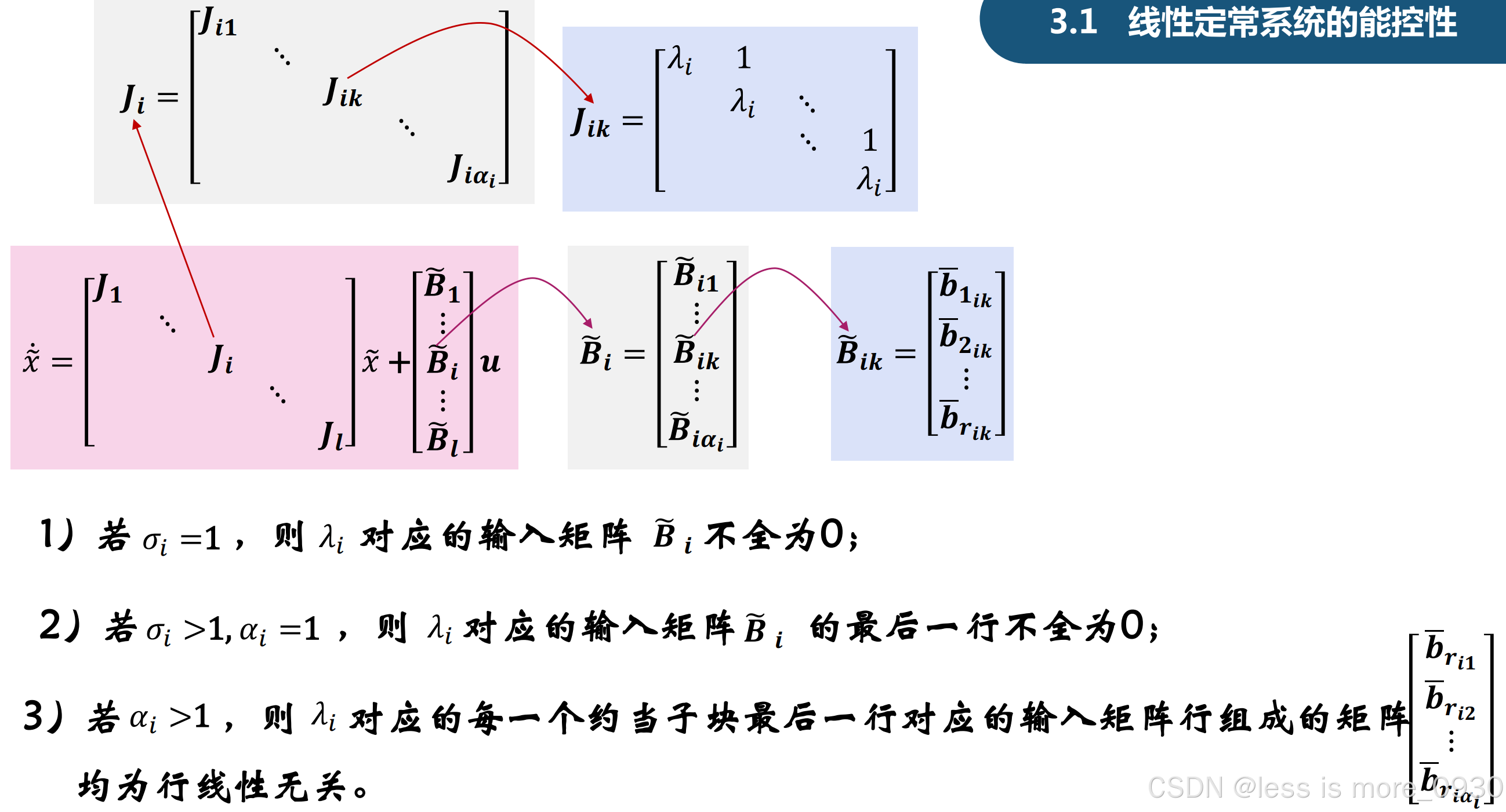
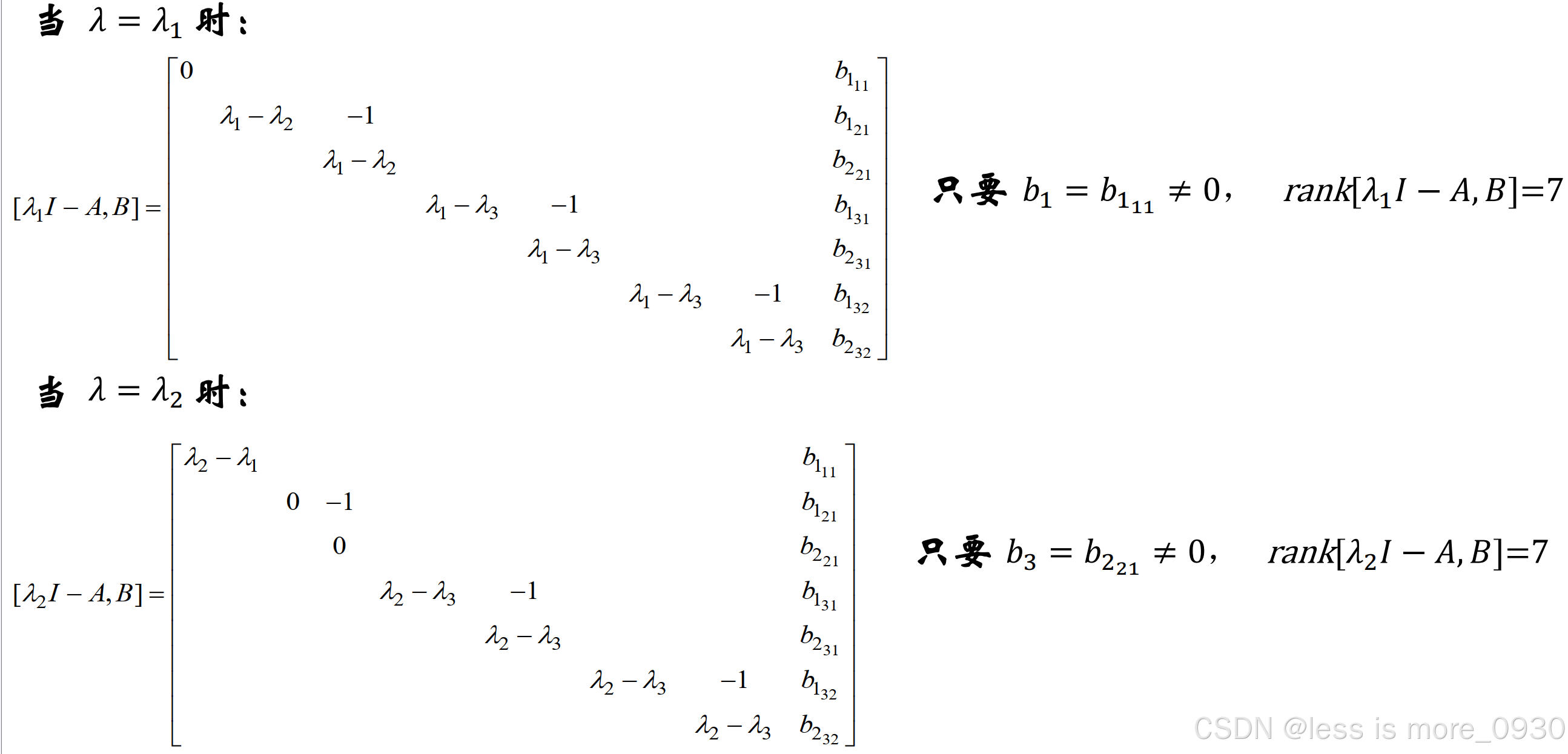
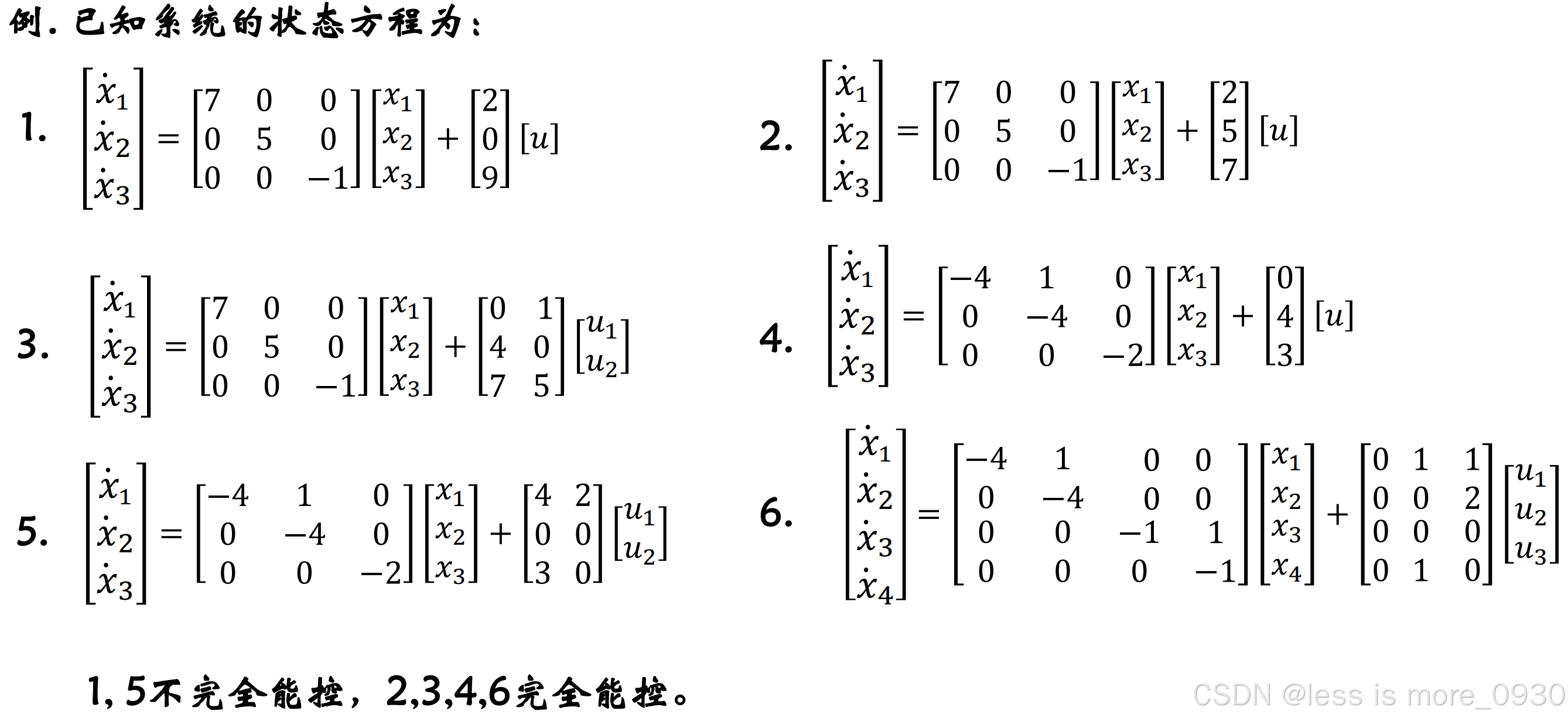
1.2 线性定常系统的能观性

1.2.1 定义

  

1.2.2 能观性Gram矩阵判据

  

1.2.3 能观性秩判据

  

1.2.4 能观性PBH判据

  

1.2.5 能观性规范型判据

  

---

1.3 线性时变系统的能控性与能观性

1.3.1 能控性定义

  

       因为线性时变系统的系数矩阵随着时间在不断的变化，因此，线性时变系统的能控性和能观性是针对某一时刻进行讨论的。

1.3.2 能控性Gram矩阵判据

  

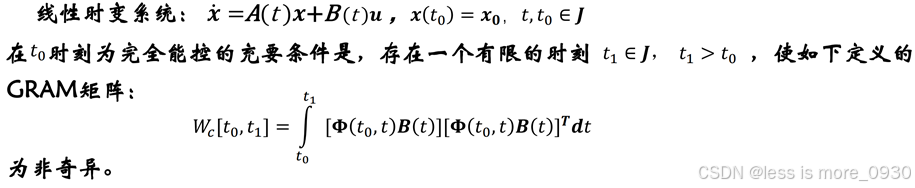
       线性时变系统的状态转移矩阵无法写出封闭形式，因此，线性时变系统的Gram矩阵判据只具有理论意义。

1.3.3 能控性秩判据

1.3.4 能观性定义

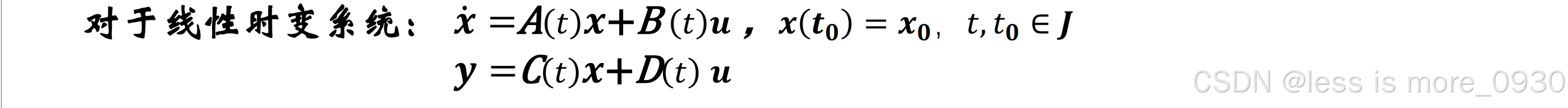
1.3.5 能观性Gram矩阵判据

  

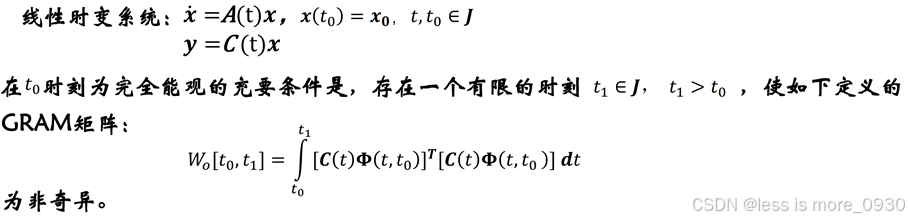
1.3.6 能观性秩判据