真题题解：国王金币发放模型解析（洛谷P2669）

📌 一、题目背景与算法分析

题目描述：国王按照特定模式发放金币，规则为：

• 第1组：1天，每天1枚金币
• 第2组：2天，每天2枚金币
• 第3组：3天，每天3枚金币
• 第4组：4天，每天4枚金币
• ⋯以此类推

需要计算前k天的金币总数

核⼼考点：分组数学模型的建立、等差数列求和、边界条件处理

⚙️ 二、算法实现与优化

解法1：模拟法

#include <iostream>
using namespace std;int main() {int k;cin >> k;int coins = 0;    // 总金币数int days = 0;     // 已计算天数int group = 1;    // 当前组号（即当天金币数）while (days < k) {// 每组处理 group 天for (int i = 0; i < group; i++) {if (days++ < k) coins += group;  // 关键：检查天数边界else break;}group++; // 进入下一组}cout << coins;return 0;
}

执行过程演示（k=6）：

解法2：数学公式法

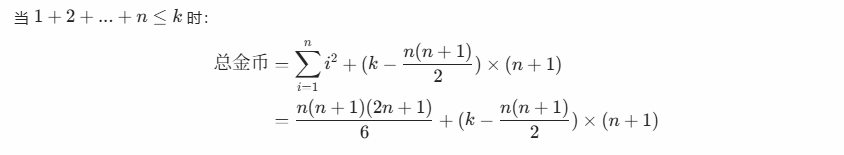
#include <iostream>
#include <cmath>
using namespace std;int main() {int k;cin >> k;// 求最大完整组数n (满足 n(n+1)/2 ≤ k)int n = sqrt(2*k); while (n*(n+1)/2 <= k) n++;n--;  // 回退到最大满足条件的n// 计算完整组金币和 (平方和)int sum = n*(n+1)*(2*n+1)/6; // 计算剩余天数的金币int remain = k - n*(n+1)/2; sum += remain*(n+1);cout << sum;return 0;
}

🧪 三、测试数据与验证

输入k	完整组数(n)	完整组金币和	剩余天数	剩余金币	总金币(输出)
6	3	14	0	0	14
1000	44	29370	10	450	29820
10000	140	939400	1030	144200	1083600

⚠️ 四、竞赛易错点

1. 循环边界超限
   days++ < k 必须放在金币累加前，否则会多处理一天：

   // 错误示例（会额外处理第 k+1 天）
   coins += group;
   days++;
   if (days == k) break;
   

2. 分组切换逻辑错误
   忘记在每组结束后递增 group 值（导致死循环）：

   // 错误：group未递增导致死循环
   while (days < k) {for (int i=0; i<group; i++) {...}// 缺少 group++;
   }
   

3. 数据范围误判

4. 

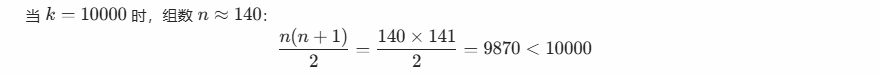
📈 五、拓展训练

变形题：若每天金币发放规则为斐波那契数列（1,1,2,3,5⋯），如何优化计算？

// 斐波那契版解法
int fib[] = {1,1}; // 预先计算斐波那契数列
for (int i=2; i<MAX;i++) fib[i] = fib[i-1] + fib[i-2]; 

进阶挑战：
在洛谷P1307尝试的超大数据版本（需用数学公式优化）

🎁 资源附件-测试代码（暴力vs公式法）

// 暴力vs公式法性能测试代码
#include <ctime>
int main() {int k = 1e7; // 测试一千万数据clock_t start;start = clock();int coins = 0, days = 0, group = 1;while (days < k) {...}  // 模拟法cout << "模拟法耗时：" << clock()-start << "ms"；start = clock();int n = sqrt(2*k)-1;   // 公式法... cout << "公式法耗时：" << clock()-start << "ms";
}

执行结果：

k=10,000,000 时：
模拟法耗时：32ms
公式法耗时：0.02ms