当前位置：首页 > news >正文

【循环神经网络3】门控循环单元GRU详解

news 2025/9/29 8:25:12

1 GRU的提出背景

GRU提出的Motivation是为了解决传统RNN（1986）中在处理实际问题时遇到的长期记忆丢失和反向传播中的梯度消失或爆炸（详见【循环神经网络1】一文搞定RNN入门与详解-CSDN博客的4.4节）等问题。

相较于LSTM（1997），GRU于更晚的2014年由论文1412.3555提出，其优势在于能用更少的计算资源得到于LSTM几乎相当的效果。

GRU模型通过引入门控机制，可以更好地控制信息的流动，并有效地缓解梯度消失和梯度爆炸问题。这使得网络能够更好地捕捉到长期依赖关系，提高模型的性能和泛化能力。

2 GRU的原理与结构

2.1 重置门和更新门

GRU引入了两个最重要的门控单元：

重置门（reset gate）控制”可能还想记住”的过去状态的数量。
更新门（update gate）控制新状态中有多少个旧状态的副本。

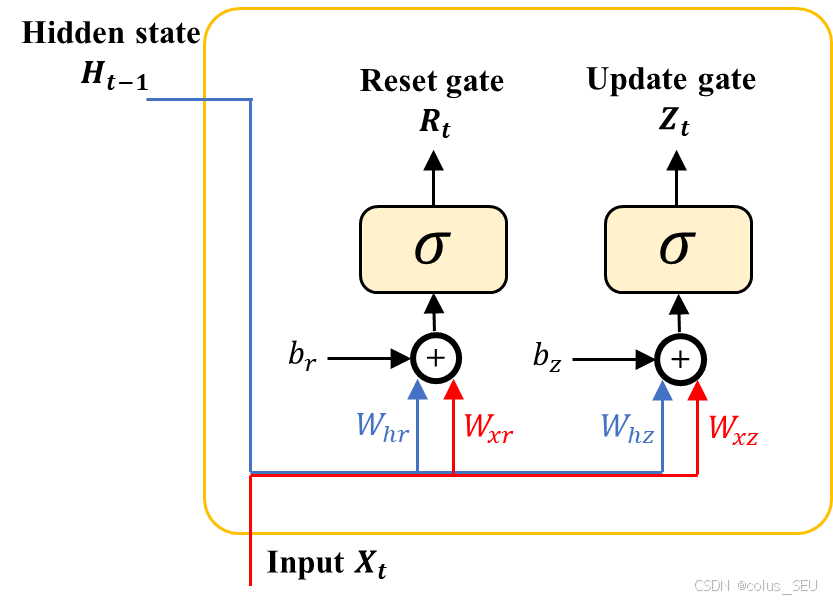
GRU 的数学有如下的形式化描述，对于给定的时间步 t，假设输入一个小批量 $\mathbf{X}_t \in \mathbb{R}^{n \times d}$ （其中 n 表示样本数，d 表示输入数），前一个时间步的隐状态是 $\mathbf{H}_{t-1} \in \mathbb{R}^{n \times h}$ （其中 h 表示隐藏单元数），则重置门 $\mathbf{R}_t \in \mathbb{R}^{n \times h}$ 和更新门 $\mathbf{Z}_t \in \mathbb{R}^{n \times h}$ 的计算如下所示：

$\mathbf{R}_t = \sigma(\mathbf{X}_t \mathbf{W}_{xr} + \mathbf{H}_{t-1} \mathbf{W}_{hr} + b_r)$

$\mathbf{Z}_t = \sigma(\mathbf{X}_t \mathbf{W}_{xz} + \mathbf{H}_{t-1} \mathbf{W}_{hz} + b_z)$

以上 $\mathbf{R}_t$ 和 $\mathbf{Z}_t$ 的计算步骤相同，这里拿 $\mathbf{R}_t$ 举例：

$\mathbf{W}_{xr} \in \mathbb{R}^{d \times h}$ 用于和输入 $\mathbf{X}_t$ 做矩阵乘法，得到一个大小为 $\mathbb{R}^{n \times h}$ 的矩阵；
$\mathbf{W}_{hr} \in \mathbb{R}^{d \times h}$ 用于和上一时间步的隐状态做矩阵乘法，得到一个大小为 $\mathbb{R}^{n \times h}$ 的矩阵；
$b_r \in \mathbb{R}^{1 \times h}$ 是一个向量，与前面两个得到的矩阵相加时 torch 中“广播机制”会把 $b_r$ 扩充为相同 n 行。
然后将计算结果通过激活函数 sigmoid 将每个元素映射到 (0, 1) 区间，用来充当遗忘门控信号。
最后得到一个矩阵，大小不变 $\mathbf{R}_t \in \mathbb{R}^{n \times h}$ ，维度 1 是 batch 的大小，维度 2 是隐层节点数，该矩阵的每个元素相当于一个遗忘信号，控制与 $\mathbf{H}_{t-1}$ 对应位置上的元素，决定了记住上一时间步信息的比例。例如，当 $r_t = 1 \in \mathbf{R}_t$ 表示上一时间步的隐状态全部拿去作后续计算；当 $r_t = 0 \in \mathbf{R}_t$ 表示上一时间步的隐状态全部拿去作后续计算。

从上面 5 个计算步可以看出，本小结一共有六组要学习的参数：

重置门 $\mathbf{R}_t$ 对应参数 $\mathbf{W}_{xr}, \mathbf{W}_{hr}, b_r$ ，参数个数分别为 $d \times h$ ， $d \times h$ 和 $h$ 。
更新门 $\mathbf{Z}_t$ 对应参数 $\mathbf{W}_{xz}, \mathbf{W}_{hz}, b_z$ ，参数个数分别为 $d \times h$ ， $d \times h$ 和 $h$ 。

因此，一共有 $4d \times h + 2h$ 个参数要通过反向传播来更新。

2.2 候选隐状态

目前为止，我们得到了重置门 $\mathbf{R}_t$ ，更新门 $\mathbf{Z}_t$ 的计算结果，但对于要更新的隐状态是如何计算的还没进行描述。在GRU中，通常先通过 $\mathbf{R}_t$ 计算得到一个候选隐状态 $\tilde{\mathbf{H}}_t$ ，然后用 $\mathbf{Z}_t$ 来决定更新的程度。

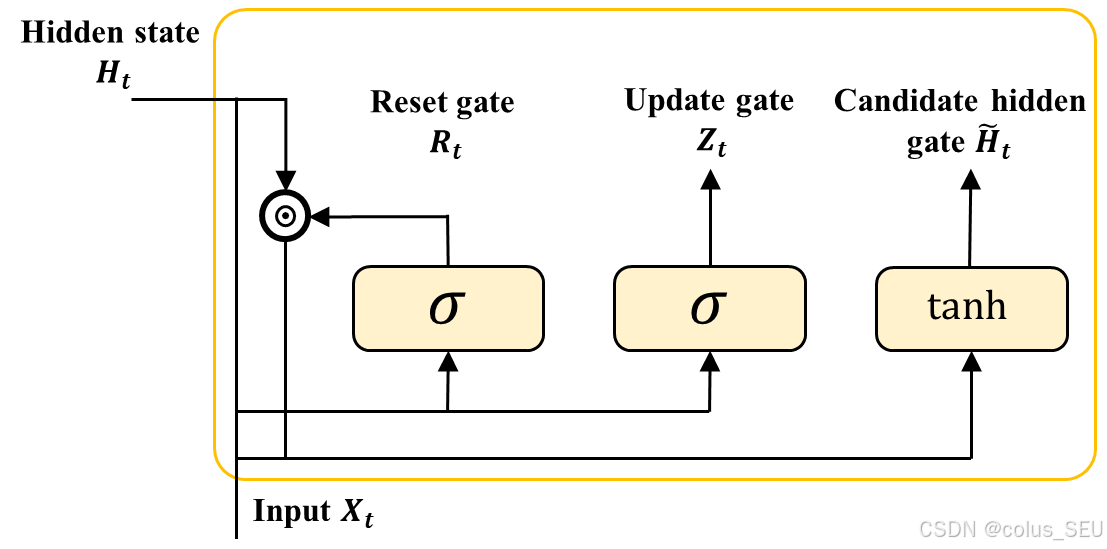
下面阐述候选隐状态的详细计算过程：

将重置信号 $\mathbf{R}_t$ 与 $\mathbf{H}_{t-1}$ 做元素乘积（哈达玛积），即 $\mathbf{R}_t \odot \mathbf{H}_{t-1}$ ，然后与 $\mathbf{W}_{hh} \in \mathbb{R}^{h \times h}$ 做矩阵乘法，得到一个大小为 $\mathbb{R}^{n \times h}$ 的矩阵，n 是 batch 的大小；
然后用 $\mathbf{W}_{xr} \in \mathbb{R}^{d \times h}$ 和输入 $\mathbf{X}_t$ 做矩阵乘法，得到一个大小为 $\mathbb{R}^{n \times h}$ 的矩阵；
同时用 $b_h \in \mathbb{R}^{1 \times h}$ 向量，与前面两个得到的矩阵相加时 torch 中“广播机制”会把 $b_h$ 扩充为相同 n 行。
最后，得到在时间步 t 的候选隐状态矩阵 $\tilde{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$ ：

$\tilde{\mathbf{H}}_t = \tanh(\mathbf{X}_t \mathbf{W}_{xh} + (\mathbf{R}_t \odot \mathbf{H}_{t-1}) \mathbf{W}_{hh} + b_h)$

其中符号 $\odot$ 表示哈达玛积运算符。这里，使用 $\tanh$ 来确保候选隐状态矩阵 $\tilde{\mathbf{H}}_t$ 中 element-wise 值映射到区间 (-1, 1) 内。

小结，从上面4个计算步可以看出，本小结一共有3组要学习的参数，分别是 $\mathbf{W}_{xh}, \mathbf{W}_{hh}, b_h$ ，参数个数分别为 $d \times h$ ， $h \times h$ 和 $h$ 。因此，一共有 $(d + h + 1)h$ 个参数要通过反向传播来更新。

注：哈达玛积的符号问题。

细心的读者可能会注意到笔者在LSTM中对哈达玛积使用的是 $\circ$ 符号，它与 $\odot$ 的区别主要在于：

在正式数学写作中，推荐使用 $\circ$ ，这是由数学界广泛接受的标准符号：

$(\mathbf{A} \circ \mathbf{B})_{ij} = A_{ij} B_{ij}$

在机器学习/深度学习论文中，\odot 非常流行（例如在 LSTM、注意力机制中常见）：

$\mathbf{h}_t = \mathbf{z} \odot \mathbf{h}_{t-1} + (1 - \mathbf{z}) \odot \tilde{\mathbf{h}}_t$

总的来说，使用 $\circ$ 和 $\odot$ 都是可行的。

2.3 隐状态更新

有了重置门 $\mathbf{R}_t$ ，更新门 $\mathbf{Z}_t$ 的计算结果，以及一个候选隐状态 $\tilde{\mathbf{H}}_t$ ，一切准备就绪后，接下来我们对进行更新操作。

通过上面的运算，我们得到了一个候选隐状态 $\tilde{\mathbf{H}}_t$ ，现在要做的是结合更新门 $\mathbf{Z}_t$ 来最终确定时间步 t 的隐状态在多大程度上由 $\mathbf{H}_{t-1}$ 和新得到的 $\tilde{\mathbf{H}}_t$ 决定。刚才我们把 $\mathbf{Z}_t$ 的每个元素都限定在了 (0, 1) 区间，此时可以做一凸组合，就像 DDPG 中的软更新一样，只不过这个控制参数 $\mathbf{Z}_t$ 是可学习的。因此，对于当前时间步的隐状态 $\mathbf{H}_t$ ，可由下式计算：

$\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t$

从该式可以看出，当 $\mathbf{Z}_t$ 趋于 0 时，新的隐状态 $\mathbf{H}_t$ 几乎来自于 $\tilde{\mathbf{H}}_t$ 。不过需要思考一下这样设计的理由。假如所有时间步的更新门 $\mathbf{Z}_t$ 都接近 1，则无论是多长的序列数据，距离当前时刻最久远的隐状态都能很好的保留到后续的计算中。To this end，我们得到一个完成 GRU 单元计算流，如下图所示（简化起见，省略了待学习参数矩阵乘法的标注）。

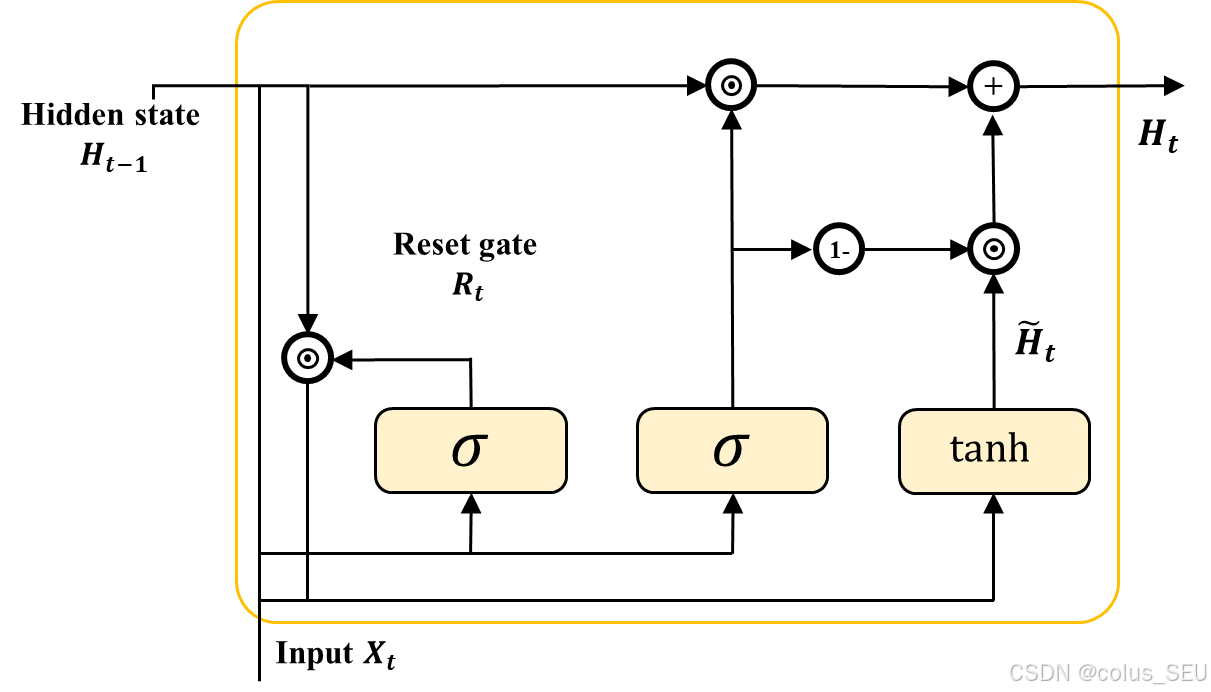
2.4 最终输出

与 RNN 相同的是，得到了当前时间步的隐状态，我们要将其映射到下游任务需要的特征维度，因此引入矩阵 $\mathbf{W}_{hq} \in \mathbb{R}^{h \times q}$ 和向量 $b_q$ 用于最后的线性层映射，其中输出的特征维度为 $q$ 。以上计算可由 (4) 表示

$\mathbf{O}_t = \mathbf{H}_t \mathbf{W}_{hq} + b_q$

重置门有助于提取序列中的短期依赖关系，更新门有助于获取序列数据的长期依赖关系。

3 GRU与LSTM的对比

【循环神经网络2】长短期记忆网络LSTM详解-CSDN博客https://blog.csdn.net/colus_SEU/article/details/152164629?spm=1001.2014.3001.5501LSTM详解如上▲

结构复杂度：
- GRU 的结构相对 LSTM 更简单，它只有两个门控机制和一个隐藏状态，
- 而 LSTM 有三个门控机制（输入门、遗忘门、输出门）和一个单元状态，
- 因此 GRU 的计算量相对较小，训练速度更快。
性能表现：
- 在大多数情况下，GRU 和 LSTM 都能很好地处理序列数据中的长期依赖问题，
- 但在某些任务中，GRU 可能因为结构简单而表现稍逊一筹，
- 而在另一些对计算资源要求较高或数据量较小的场景下，GRU 可能更具优势。