【数据结构】多项式的基本运算

一、数据结构设计

多项式采用单向链表存储，核心结构PNode定义如下：

typedef struct PNode {float coef;        // 多项式项的系数（支持浮点数）int expn;          // 多项式项的指数（整数）struct PNode *next; // 指向下一项的指针
} PNode, *Polynomial;

• 链表按指数升序排列（便于插入、合并同类项）；
• 头节点不存储实际数据，仅用于统一链表操作（简化空表判断）。

二、核心算法详解

1. 多项式创建（CreatePolyn）

// 多项式的创建：按指数升序插入
void CreatePolyn(Polynomial &P, int n) {P = new PNode;P->next = NULL;for (int i = 1; i <= n; ++i) {float coef;int expn;cout << "请输入第" << i << "项的系数和指数（格式：系数 指数）：";cin >> coef >> expn;PNode *s = createNode(coef, expn);PNode *pre = P;PNode *q = P->next;// 找到插入位置（保持升序）while (q != NULL && q->expn < s->expn) {pre = q;q = q->next;}// 处理同指数项合并if (q != NULL && q->expn == s->expn) {q->coef += s->coef;if (fabs(q->coef) < 1e-6) { // 系数为0则删除节点pre->next = q->next;delete q;}delete s;} else {s->next = q;pre->next = s;}}
}

功能：根据输入的项数和（系数，指数）对，构建按指数升序排列的多项式链表，自动合并同类项。

算法步骤：

1. 初始化头节点，链表为空（P->next = NULL）；
2. 循环读取每一项的系数和指数：
   • 创建新节点存储当前项；
   • 遍历链表找到插入位置：通过双指针pre（前驱）和q（当前），找到第一个指数大于当前项指数的节点（保持升序）；
   • 处理同类项：若找到指数相等的节点，将系数相加，若和为 0（fabs(coef) < 1e-6，处理浮点数精度），则删除该节点；
   • 插入新节点：若指数不重复，将新节点插入pre和q之间。

关键处理：

• 同类项自动合并，避免冗余存储；
• 系数为 0 的项直接删除，保证链表精简。

2. 多项式加法（AddPolyn）

// 多项式加法：Pa = Pa + Pb，释放Pb
void AddPolyn(Polynomial &Pa, Polynomial &Pb) {PNode *p1 = Pa->next;  // p1指向Pa的首元节点PNode *p2 = Pb->next;  // p2指向Pb的首元节点PNode *p3 = Pa;        // p3指向“和多项式”的当前尾节点（初始为Pa的头结点）while (p1 != NULL && p2 != NULL) {  // Pa和Pb均未遍历完if (p1->expn == p2->expn) {  // 情况1：指数相等float sum = p1->coef + p2->coef;  // 系数相加if (sum != 0) {  // 系数和不为0 → 保留该项p1->coef = sum;       // 更新Pa当前节点的系数p3->next = p1;p3 = p1;p1 = p1->next;PNode *r = p2;        // 删除Pb的当前节点p2 = p2->next;delete r;} else {  // 系数和为0 → 两项抵消，都删除PNode *r = p1;p1 = p1->next;delete r;r = p2;p2 = p2->next;delete r;}} else if (p1->expn < p2->expn) {  // 情况2：Pa当前项指数更小p3->next = p1;p3 = p1;p1 = p1->next;} else {  // 情况3：Pb当前项指数更小p3->next = p2;p3 = p2;p2 = p2->next;}}// 处理剩余未遍历完的多项式（直接链接）p3->next = (p1 != NULL) ? p1 : p2;delete Pb;  // 释放Pb的头结点
}

功能：计算两个多项式的和（Pa = Pa + Pb），结果存储在Pa中，释放Pb的内存。

算法原理：类似归并排序的 “合并” 过程，通过双指针同步遍历两个多项式，按指数大小合并节点，同类项系数相加。

算法步骤：

1. 初始化指针：p1（Pa的首元节点）、p2（Pb的首元节点）、p3（结果链表的当前尾节点，初始为Pa的头节点）；
2. 双指针遍历（p1和p2均非空时）：
   • 若指数相等：系数相加，若和非 0，则更新p1的系数并加入结果；若和为 0，则删除p1和p2节点；
   • 若p1指数更小：将p1加入结果，p1后移；
   • 若p2指数更小：将p2加入结果，p2后移；
3. 处理剩余节点：将未遍历完的多项式剩余部分直接链接到结果链表；
4. 释放Pb的头节点，避免内存泄漏。

时间复杂度：O(m + n)（m、n为两个多项式的项数）。

3. 多项式减法（SubtractPolyn）

// 多项式减法：Pa = Pa - Pb
void SubtractPolyn(Polynomial &Pa, Polynomial &Pb) {// 先创建Pb的相反数多项式Polynomial negPb = new PNode;negPb->next = NULL;PNode *p = Pb->next;PNode *q = negPb;while (p) {q->next = createNode(-p->coef, p->expn); // 系数取反q = q->next;p = p->next;}// 调用加法实现减法：Pa + (-Pb)AddPolyn(Pa, negPb);delete Pb;Pb = NULL;
}

功能：计算两个多项式的差（Pa = Pa - Pb），通过转化为加法实现。

算法原理：利用 “减法 = 加法 + 相反数”，即Pa - Pb = Pa + (-Pb)，其中-Pb是Pb的所有系数取反的多项式。

算法步骤：

1. 创建Pb的相反数多项式negPb：遍历Pb，对每个项的系数取反，指数不变；
2. 调用AddPolyn(Pa, negPb)：将Pa与negPb相加，结果即为Pa - Pb；
3. 释放Pb的内存，避免泄漏。

时间复杂度：O(m + n)（m为Pa项数，n为Pb项数）。

4. 多项式乘法（MultiplyPolyn）

// 多项式乘法：返回Pa * Pb的结果
Polynomial MultiplyPolyn(Polynomial Pa, Polynomial Pb) {Polynomial result = new PNode;result->next = NULL;if (!Pa->next || !Pb->next) return result; // 空多项式处理PNode *p1 = Pa->next;while (p1) {PNode *p2 = Pb->next;while (p2) {// 计算乘积项：系数相乘，指数相加float coef = p1->coef * p2->coef;int expn = p1->expn + p2->expn;// 插入结果多项式PNode *pre = result;PNode *q = result->next;while (q && q->expn < expn) {pre = q;q = q->next;}if (q && q->expn == expn) { // 合并同类项q->coef += coef;if (fabs(q->coef) < 1e-6) { // 系数为0则删除pre->next = q->next;delete q;}} else { // 插入新节点PNode *newNode = createNode(coef, expn);newNode->next = q;pre->next = newNode;}p2 = p2->next;}p1 = p1->next;}return result;
}

功能：计算两个多项式的积（result = Pa * Pb），返回新的多项式链表。

算法原理：基于多项式乘法分配律，即(a₀ + a₁x + ...)(b₀ + b₁x + ...) = Σ(aᵢbⱼx^(i+j))，遍历所有项的乘积并合并同类项。

算法步骤：

1. 初始化结果链表（空表）；
2. 双重循环遍历Pa和Pb的所有项：
   • 计算乘积项：系数 = p1->coef * p2->coef，指数 = p1->expn + p2->expn；
   • 插入结果链表：按指数升序找到插入位置，若存在同类项则系数相加，若和为 0 则删除节点，否则插入新节点；
3. 返回结果链表。

关键处理：

• 乘积项可能产生大量同类项，需实时合并（避免链表冗余）；
• 空多项式（某一多项式无项）直接返回空表。

时间复杂度：O(m*n)（m、n为两个多项式的项数，最坏情况无同类项）。

5. 多项式除法（DividePolyn）

// 多项式除法：返回商多项式，余数通过引用返回
Polynomial DividePolyn(Polynomial Pa, Polynomial Pb, Polynomial &remainder) {Polynomial quotient = new PNode;quotient->next = NULL;remainder = new PNode;remainder->next = NULL;// 复制被除数到余数PNode *p = Pa->next;PNode *r = remainder;while (p) {r->next = createNode(p->coef, p->expn);r = r->next;p = p->next;}PNode *divisorHigh = getHighestTerm(Pb);if (!divisorHigh) { // 除数为空cerr << "除数不能为零多项式！" << endl;return quotient;}int divisorExp = divisorHigh->expn;float divisorCoef = divisorHigh->coef;while (true) {PNode *remainderHigh = getHighestTerm(remainder);if (!remainderHigh || remainderHigh->expn < divisorExp) {break; // 余数次数小于除数次数，结束除法}// 计算商项：(余数最高项)/(除数最高项)float qCoef = remainderHigh->coef / divisorCoef;int qExp = remainderHigh->expn - divisorExp;// 将商项插入商多项式PNode *pre = quotient;PNode *q = quotient->next;while (q && q->expn < qExp) {pre = q;q = q->next;}PNode *qNode = createNode(qCoef, qExp);qNode->next = q;pre->next = qNode;// 计算：余数 = 余数 - (商项 * 除数)Polynomial temp = new PNode;temp->next = NULL;PNode *pb = Pb->next;while (pb) {PNode *term = createNode(qCoef * pb->coef, qExp + pb->expn);term->next = temp->next;temp->next = term;pb = pb->next;}// 余数 = 余数 - tempPolynomial negTemp = new PNode;negTemp->next = NULL;PNode *t = temp->next;while (t) {negTemp->next = createNode(-t->coef, t->expn);negTemp = negTemp->next;t = t->next;}AddPolyn(remainder, negTemp);DestroyPolyn(temp);}return quotient;
}

功能：计算两个多项式的商和余数（Pa = 商 * Pb + 余数），商通过返回值返回，余数通过引用参数返回。

算法原理：模拟数学中的 “长除法”，核心是反复用余数的最高次项除以除数的最高次项，得到商项，再更新余数，直到余数的次数小于除数的次数。

算法步骤：

1. 初始化：余数初始化为Pa的副本，商初始为空表；
2. 获取除数的最高次项（divisorHigh）：若除数为空多项式，输出错误；
3. 循环计算商项（直到余数次数 < 除数次数）：
   • 取余数的最高次项（remainderHigh）；
   • 计算商项：系数 = remainderHigh->coef / divisorHigh->coef，指数 = remainderHigh->expn - divisorHigh->expn，插入商链表；
   • 更新余数：余数 = 余数 - (商项 * 除数)（通过乘法和减法实现）；
4. 返回商链表，余数通过引用传出。

关键处理：

• 除数为零多项式时直接报错（数学上无意义）；
• 余数次数必须小于除数次数才终止循环；
• 商项按指数升序插入，保证链表有序。

时间复杂度：O(k*m*n)（k为商的项数，m、n为被除数和除数的项数）。

三、辅助算法

1.创建新节点

// 辅助函数：创建新节点
PNode* createNode(float coef, int expn) {PNode *node = new PNode;node->coef = coef;node->expn = expn;node->next = NULL;return node;
}

功能：创建一个包含指定系数（coef）和指数（expn）的多项式项节点，并返回该节点的指针。每个节点代表多项式中的一项（如 3.5x² 中的系数 3.5 和指数 2）。

算法步骤：

1. 动态分配内存通过 new PNode 在堆上为新节点分配内存空间。选择堆内存而非栈内存，是因为多项式节点需要在函数调用结束后继续存在（用于构建链表），而栈内存会在函数返回后自动释放。

2. 初始化节点成员

   • 系数赋值：node->coef = coef，将输入的系数存储到节点中（支持浮点数，如 2.5、-3.0 等）。
   • 指数赋值：node->expn = expn，将输入的指数存储到节点中（整数，如 0、3 等，对应常数项或 x³ 项）。
   • 指针初始化：node->next = NULL，新节点暂时未链接到其他节点，因此 next 指针设为 NULL（避免野指针，确保链表操作安全）。

3. 返回节点指针返回指向新创建节点的指针，供调用者（如 CreatePolyn、CopyPolyn 等函数）将其插入到多项式链表中。

2.获取多项式最高次项

// 辅助函数：获取多项式最高次项
PNode* getHighestTerm(Polynomial P) {if (!P->next) return NULL;PNode *p = P->next;while (p->next) p = p->next;return p;
}

功能：在一个按指数升序排列的多项式链表中，找到并返回最高次项的节点指针。最高次项即多项式中指数最大的项（如 3x⁵ + 2x² + 1 中的 3x⁵）。

算法步骤：

1. 判断多项式是否为空检查链表头节点的下一个节点（P->next）是否为 NULL：

   • 若 P->next == NULL，说明多项式没有任何项（空多项式），直接返回 NULL。
   • 若 P->next != NULL，说明多项式非空，继续执行。

2. 定位最高次项

   • 初始化指针 p 为第一个有效项（p = P->next），即链表的首元节点。
   • 循环遍历链表：while (p->next) p = p->next;该循环的逻辑是：只要当前节点 p 有下一个节点（p->next != NULL），就将 p 移动到下一个节点。当循环结束时，p 指向链表的最后一个节点（因为最后一个节点的 next 为 NULL），而根据升序存储约定，这个节点就是最高次项。

3. 返回最高次项节点返回指针 p，即最高次项的节点地址。

3. 多项式复制（CopyPolyn）

// 复制多项式（用于测试除法时保护原多项式）
Polynomial CopyPolyn(Polynomial P) {Polynomial copy = new PNode;copy->next = NULL;PNode *p = P->next;PNode *q = copy;while (p) {q->next = createNode(p->coef, p->expn);q = q->next;p = p->next;}return copy;
}

功能：创建一个与原多项式完全相同的新链表（深拷贝），避免原多项式被修改。

算法步骤：

• 初始化新链表头节点；
• 遍历原多项式，为每个项创建新节点（复制系数和指数），链接到新链表；
• 返回新链表。

4. 多项式销毁（DestroyPolyn）

// 销毁多项式
void DestroyPolyn(Polynomial &P) {PNode *curr = P;while (curr) {PNode *next = curr->next;delete curr;curr = next;}P = NULL;
}

功能：释放多项式链表的所有节点，避免内存泄漏。

算法步骤：

• 遍历链表，用next指针保存下一个节点；
• 逐个删除当前节点，最终将头指针置空（避免野指针）。

5. 多项式打印（PrintPolyn）

// 打印多项式（降序输出）
void PrintPolyn(Polynomial P) {if (!P->next) {cout << "0" << endl;return;}// 收集所有项到数组int count = 0;PNode *p = P->next;while (p) {count++;p = p->next;}pair<float, int> *terms = new pair<float, int>[count];p = P->next;for (int i = 0; i < count; i++) {terms[i] = {p->coef, p->expn};p = p->next;}// 降序输出bool first = true;for (int i = count - 1; i >= 0; i--) {float coef = terms[i].first;int expn = terms[i].second;if (fabs(coef) < 1e-6) continue;if (first) {first = false;if (coef < 0) cout << "-";} else {if (coef > 0) cout << " + ";else cout << " - ";}// 输出系数（绝对值）float absCoef = fabs(coef);if (fabs(absCoef - 1) > 1e-6 || expn == 0) {cout << absCoef;}// 输出指数部分if (expn > 0) {cout << "x";if (expn != 1) cout << "^" << expn;}}cout << endl;delete[] terms;
}

功能：按降序输出多项式（符合人类阅读习惯），简化系数和指数的显示（如1x显示为x，x^1显示为x）。

算法步骤：

1. 收集所有项到数组（因链表是升序，数组便于逆序遍历）；
2. 逆序遍历数组（实现降序输出）：
   • 跳过系数为 0 的项；
   • 处理符号：首项正系数不显示+，负系数显示-；中间项正系数显示+，负系数显示-；
   • 简化显示：系数为±1且非常数项时省略1，指数为1时省略^1。

四、算法特点总结

1. 链表有序性：所有操作均保持链表按指数升序排列，简化插入、合并同类项的逻辑；
2. 内存安全：所有动态分配的节点均在销毁函数中释放，避免内存泄漏；
3. 浮点数处理：通过fabs(coef) < 1e-6判断系数是否为 0，处理浮点数精度误差；
4. 边界覆盖：支持空多项式、零多项式（除除法外）、常数项等特殊情况；
5. 操作直观：打印函数按降序输出，符合数学表达式的阅读习惯。

五、完整代码实现

（一）C++代码如下：

#include <iostream>
#include <cmath>
using namespace std;// 多项式节点结构定义
typedef struct PNode {float coef;        // 系数int expn;          // 指数struct PNode *next; // 下一个节点
} PNode, *Polynomial;// 辅助函数：创建新节点
PNode* createNode(float coef, int expn);
// 多项式的创建：按指数升序插入
void CreatePolyn(Polynomial &P, int n);
// 多项式加法：Pa = Pa + Pb，释放Pb
void AddPolyn(Polynomial &Pa, Polynomial &Pb);
// 多项式减法：Pa = Pa - Pb
void SubtractPolyn(Polynomial &Pa, Polynomial &Pb);
// 多项式乘法：返回Pa * Pb的结果
Polynomial MultiplyPolyn(Polynomial Pa, Polynomial Pb);
// 辅助函数：获取多项式最高次项
PNode* getHighestTerm(Polynomial P);
// 多项式除法：返回商多项式，余数通过引用返回
Polynomial DividePolyn(Polynomial Pa, Polynomial Pb, Polynomial &remainder);
// 打印多项式（降序输出）
void PrintPolyn(Polynomial P);
// 销毁多项式
void DestroyPolyn(Polynomial &P);
// 复制多项式（用于测试除法时保护原多项式）
Polynomial CopyPolyn(Polynomial P);
int main() {Polynomial Pa = NULL, Pb = NULL, Pc = NULL, remainder = NULL;int n1, n2;// 创建多项式Pacout << "===== 创建多项式 Pa =====" << endl;cout << "请输入Pa的项数：";cin >> n1;CreatePolyn(Pa, n1);cout << "Pa = ";PrintPolyn(Pa);// 创建多项式Pbcout << "\n===== 创建多项式 Pb =====" << endl;cout << "请输入Pb的项数：";cin >> n2;CreatePolyn(Pb, n2);cout << "Pb = ";PrintPolyn(Pb);// 加法Polynomial PaAdd = CopyPolyn(Pa);Polynomial PbAdd = CopyPolyn(Pb);AddPolyn(PaAdd, PbAdd);cout << "\n加法：Pa + Pb = ";PrintPolyn(PaAdd);DestroyPolyn(PaAdd);// 减法Polynomial PaSub = CopyPolyn(Pa);Polynomial PbSub = CopyPolyn(Pb);SubtractPolyn(PaSub, PbSub);cout << "减法：Pa - Pb = ";PrintPolyn(PaSub);DestroyPolyn(PaSub);// 乘法Polynomial product = MultiplyPolyn(Pa, Pb);cout << "乘法：Pa * Pb = ";PrintPolyn(product);// 除法Polynomial PaDiv = CopyPolyn(Pa);Polynomial PbDiv = CopyPolyn(Pb);Polynomial quotient = DividePolyn(PaDiv, PbDiv, remainder);cout << "除法：Pa / Pb = ";PrintPolyn(quotient);cout << "余数：";PrintPolyn(remainder);// 释放内存DestroyPolyn(Pa);DestroyPolyn(Pb);DestroyPolyn(product);DestroyPolyn(quotient);DestroyPolyn(remainder);return 0;
}
// 辅助函数：创建新节点
PNode* createNode(float coef, int expn) {PNode *node = new PNode;node->coef = coef;node->expn = expn;node->next = NULL;return node;
}// 多项式的创建：按指数升序插入
void CreatePolyn(Polynomial &P, int n) {P = new PNode;P->next = NULL;for (int i = 1; i <= n; ++i) {float coef;int expn;cout << "请输入第" << i << "项的系数和指数（格式：系数 指数）：";cin >> coef >> expn;PNode *s = createNode(coef, expn);PNode *pre = P;PNode *q = P->next;// 找到插入位置（保持升序）while (q != NULL && q->expn < s->expn) {pre = q;q = q->next;}// 处理同指数项合并if (q != NULL && q->expn == s->expn) {q->coef += s->coef;if (fabs(q->coef) < 1e-6) { // 系数为0则删除节点pre->next = q->next;delete q;}delete s;} else {s->next = q;pre->next = s;}}
}// 多项式加法：Pa = Pa + Pb，释放Pb
void AddPolyn(Polynomial &Pa, Polynomial &Pb) {PNode *p1 = Pa->next;  // p1指向Pa的首元节点PNode *p2 = Pb->next;  // p2指向Pb的首元节点PNode *p3 = Pa;        // p3指向“和多项式”的当前尾节点（初始为Pa的头结点）while (p1 != NULL && p2 != NULL) {  // Pa和Pb均未遍历完if (p1->expn == p2->expn) {  // 情况1：指数相等float sum = p1->coef + p2->coef;  // 系数相加if (sum != 0) {  // 系数和不为0 → 保留该项p1->coef = sum;       // 更新Pa当前节点的系数p3->next = p1;p3 = p1;p1 = p1->next;PNode *r = p2;        // 删除Pb的当前节点p2 = p2->next;delete r;} else {  // 系数和为0 → 两项抵消，都删除PNode *r = p1;p1 = p1->next;delete r;r = p2;p2 = p2->next;delete r;}} else if (p1->expn < p2->expn) {  // 情况2：Pa当前项指数更小p3->next = p1;p3 = p1;p1 = p1->next;} else {  // 情况3：Pb当前项指数更小p3->next = p2;p3 = p2;p2 = p2->next;}}// 处理剩余未遍历完的多项式（直接链接）p3->next = (p1 != NULL) ? p1 : p2;delete Pb;  // 释放Pb的头结点
}// 多项式减法：Pa = Pa - Pb
void SubtractPolyn(Polynomial &Pa, Polynomial &Pb) {// 先创建Pb的相反数多项式Polynomial negPb = new PNode;negPb->next = NULL;PNode *p = Pb->next;PNode *q = negPb;while (p) {q->next = createNode(-p->coef, p->expn); // 系数取反q = q->next;p = p->next;}// 调用加法实现减法：Pa + (-Pb)AddPolyn(Pa, negPb);delete Pb;Pb = NULL;
}// 多项式乘法：返回Pa * Pb的结果
Polynomial MultiplyPolyn(Polynomial Pa, Polynomial Pb) {Polynomial result = new PNode;result->next = NULL;if (!Pa->next || !Pb->next) return result; // 空多项式处理PNode *p1 = Pa->next;while (p1) {PNode *p2 = Pb->next;while (p2) {// 计算乘积项：系数相乘，指数相加float coef = p1->coef * p2->coef;int expn = p1->expn + p2->expn;// 插入结果多项式PNode *pre = result;PNode *q = result->next;while (q && q->expn < expn) {pre = q;q = q->next;}if (q && q->expn == expn) { // 合并同类项q->coef += coef;if (fabs(q->coef) < 1e-6) { // 系数为0则删除pre->next = q->next;delete q;}} else { // 插入新节点PNode *newNode = createNode(coef, expn);newNode->next = q;pre->next = newNode;}p2 = p2->next;}p1 = p1->next;}return result;
}// 辅助函数：获取多项式最高次项
PNode* getHighestTerm(Polynomial P) {if (!P->next) return NULL;PNode *p = P->next;while (p->next) p = p->next;return p;
}// 多项式除法：返回商多项式，余数通过引用返回
Polynomial DividePolyn(Polynomial Pa, Polynomial Pb, Polynomial &remainder) {Polynomial quotient = new PNode;quotient->next = NULL;remainder = new PNode;remainder->next = NULL;// 复制被除数到余数PNode *p = Pa->next;PNode *r = remainder;while (p) {r->next = createNode(p->coef, p->expn);r = r->next;p = p->next;}PNode *divisorHigh = getHighestTerm(Pb);if (!divisorHigh) { // 除数为空cerr << "除数不能为零多项式！" << endl;return quotient;}int divisorExp = divisorHigh->expn;float divisorCoef = divisorHigh->coef;while (true) {PNode *remainderHigh = getHighestTerm(remainder);if (!remainderHigh || remainderHigh->expn < divisorExp) {break; // 余数次数小于除数次数，结束除法}// 计算商项：(余数最高项)/(除数最高项)float qCoef = remainderHigh->coef / divisorCoef;int qExp = remainderHigh->expn - divisorExp;// 将商项插入商多项式PNode *pre = quotient;PNode *q = quotient->next;while (q && q->expn < qExp) {pre = q;q = q->next;}PNode *qNode = createNode(qCoef, qExp);qNode->next = q;pre->next = qNode;// 计算：余数 = 余数 - (商项 * 除数)Polynomial temp = new PNode;temp->next = NULL;PNode *pb = Pb->next;while (pb) {PNode *term = createNode(qCoef * pb->coef, qExp + pb->expn);term->next = temp->next;temp->next = term;pb = pb->next;}// 余数 = 余数 - tempPolynomial negTemp = new PNode;negTemp->next = NULL;PNode *t = temp->next;while (t) {negTemp->next = createNode(-t->coef, t->expn);negTemp = negTemp->next;t = t->next;}AddPolyn(remainder, negTemp);DestroyPolyn(temp);}return quotient;
}// 打印多项式（降序输出）
void PrintPolyn(Polynomial P) {if (!P->next) {cout << "0" << endl;return;}// 收集所有项到数组int count = 0;PNode *p = P->next;while (p) {count++;p = p->next;}pair<float, int> *terms = new pair<float, int>[count];p = P->next;for (int i = 0; i < count; i++) {terms[i] = {p->coef, p->expn};p = p->next;}// 降序输出bool first = true;for (int i = count - 1; i >= 0; i--) {float coef = terms[i].first;int expn = terms[i].second;if (fabs(coef) < 1e-6) continue;if (first) {first = false;if (coef < 0) cout << "-";} else {if (coef > 0) cout << " + ";else cout << " - ";}// 输出系数（绝对值）float absCoef = fabs(coef);if (fabs(absCoef - 1) > 1e-6 || expn == 0) {cout << absCoef;}// 输出指数部分if (expn > 0) {cout << "x";if (expn != 1) cout << "^" << expn;}}cout << endl;delete[] terms;
}// 销毁多项式
void DestroyPolyn(Polynomial &P) {PNode *curr = P;while (curr) {PNode *next = curr->next;delete curr;curr = next;}P = NULL;
}// 复制多项式（用于测试除法时保护原多项式）
Polynomial CopyPolyn(Polynomial P) {Polynomial copy = new PNode;copy->next = NULL;PNode *p = P->next;PNode *q = copy;while (p) {q->next = createNode(p->coef, p->expn);q = q->next;p = p->next;}return copy;
}

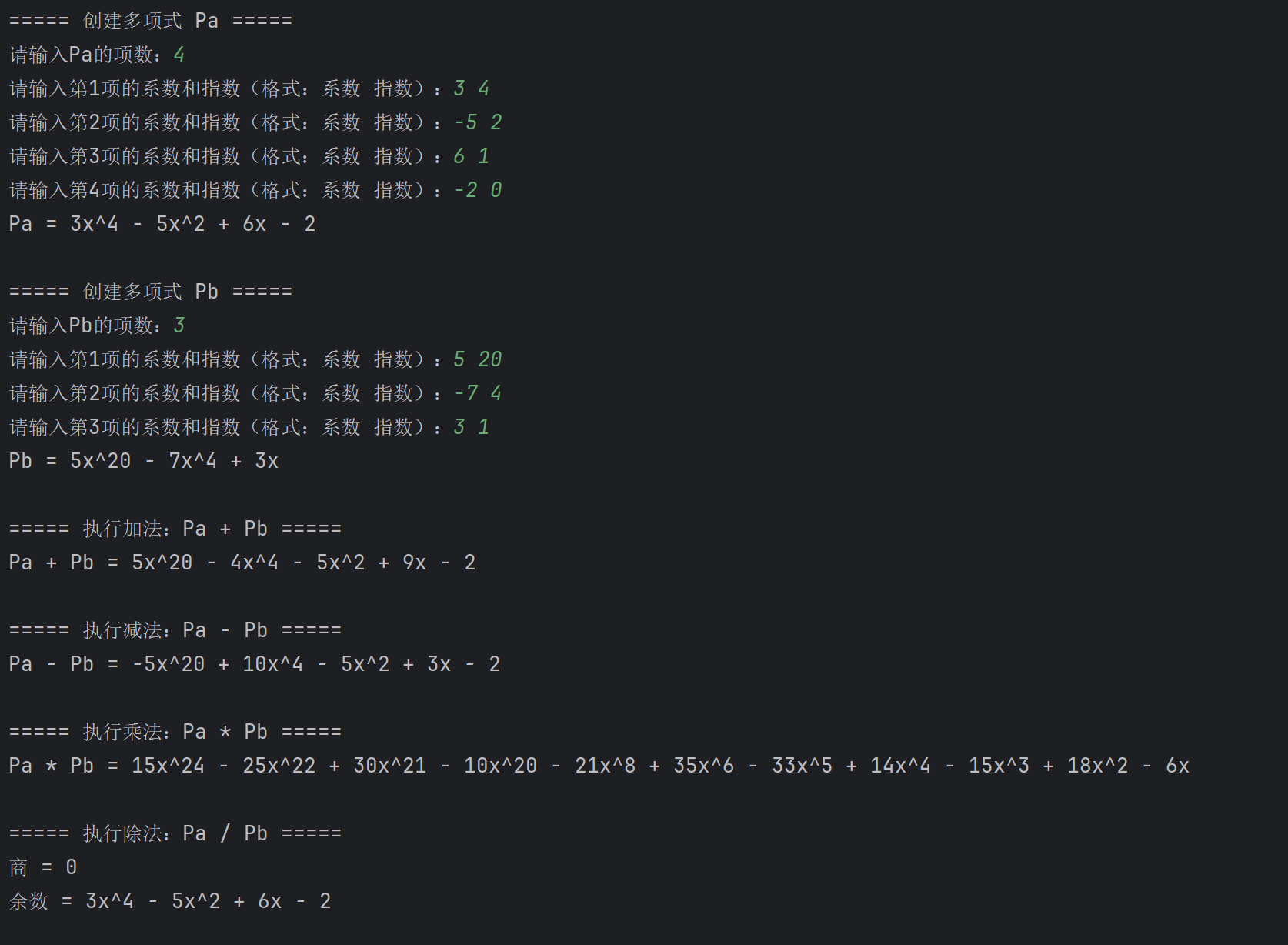
程序运行结果如下：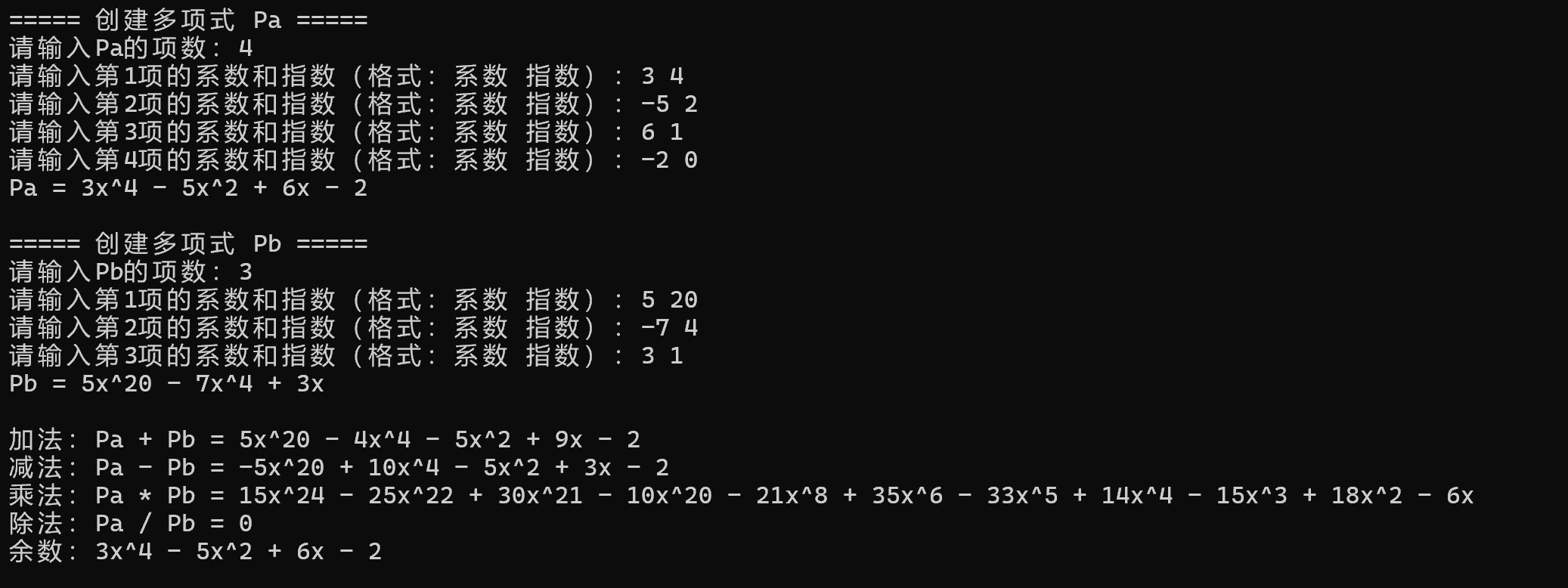

（二）Python代码如下：

class PNode:"""多项式节点类（模拟C++结构体PNode）对应C++的struct PNode，用对象属性存储系数、指数，用next引用替代指针"""def __init__(self, coef: float, expn: int):self.coef = coef    # 多项式项系数（浮点数，对应C++的float）self.expn = expn    # 多项式项指数（整数，对应C++的int）self.next = None    # 下一个节点引用（对应C++的PNode*）def createNode(coef: float, expn: int) -> PNode:"""辅助函数：创建多项式节点（对应C++的createNode函数）参数：coef（系数）、expn（指数）返回：新创建的节点对象"""return PNode(coef, expn)def CreatePolyn(P: list[PNode], n: int) -> None:"""多项式创建：按指数升序插入，自动合并同类项（对应C++的CreatePolyn）参数：P（存储多项式头节点的列表，用列表模拟引用传递）、n（多项式项数）说明：Python无指针引用，用列表包裹头节点实现"引用传递""""# 创建头节点（C++的P = new PNode; P->next = NULL）head = PNode(coef=0.0, expn=-1)  # 头节点指数设为-1（无实际意义，仅用于统一操作）head.next = NoneP.append(head)  # 将头节点存入列表，实现"引用传递"for i in range(1, n + 1):# 输入当前项的系数和指数（模拟C++的cin >> coef >> expn）while True:try:input_str = input(f"请输入第{i}项的系数和指数（格式：系数 指数）：")coef, expn = map(float, input_str.split())expn = int(expn)  # 指数强制转为整数breakexcept ValueError:print("输入格式错误！请按「数字 数字」格式输入（例：3.5 2 或 -2 1）")s = createNode(coef, expn)pre = head          # 前驱节点（对应C++的PNode* pre = P）q = head.next       # 当前节点（对应C++的PNode* q = P->next）# 找到插入位置：保持指数升序（对应C++的while循环）while q is not None and q.expn < s.expn:pre = qq = q.next# 处理同指数项合并（对应C++的if (q != NULL && q->expn == s->expn)）if q is not None and q.expn == s.expn:q.coef += s.coef# 系数接近0时删除节点（处理浮点数精度，对应C++的fabs(q->coef) < 1e-6）if abs(q.coef) < 1e-6:pre.next = q.next# Python无需手动delete（垃圾回收自动处理）# 释放s节点（此处s未插入，直接丢弃即可）else:# 插入新节点到pre和q之间（对应C++的s->next = q; pre->next = s）s.next = qpre.next = sdef AddPolyn(Pa: list[PNode], Pb: list[PNode]) -> None:"""多项式加法：Pa = Pa + Pb，释放Pb内存（对应C++的AddPolyn）参数：Pa（第一个多项式头节点列表）、Pb（第二个多项式头节点列表）说明：结果存储在Pa中，Pb后续不可用"""p1 = Pa[0].next  # Pa的首元节点（对应C++的PNode* p1 = Pa->next）p2 = Pb[0].next  # Pb的首元节点（对应C++的PNode* p2 = Pb->next）p3 = Pa[0]       # 结果链表尾节点（对应C++的PNode* p3 = Pa）while p1 is not None and p2 is not None:if p1.expn == p2.expn:# 同类项系数相加（对应C++的float sum = p1->coef + p2->coef）sum_coef = p1.coef + p2.coefif abs(sum_coef) > 1e-6:  # 系数非零（对应C++的sum != 0）p1.coef = sum_coefp3.next = p1p3 = p1p1 = p1.next# 删除Pb的当前节点（对应C++的delete r）r = p2p2 = p2.next# Python无需手动deleteelse:# 系数为零，删除Pa和Pb的当前节点（对应C++的delete r）r = p1p1 = p1.next# 无需手动deleter = p2p2 = p2.next# 无需手动deleteelif p1.expn < p2.expn:# Pa当前项指数更小，加入结果（对应C++的p3->next = p1）p3.next = p1p3 = p1p1 = p1.nextelse:# Pb当前项指数更小，加入结果（对应C++的p3->next = p2）p3.next = p2p3 = p2p2 = p2.next# 处理剩余未遍历的节点（对应C++的p3->next = (p1 != NULL) ? p1 : p2）p3.next = p1 if p1 is not None else p2# 释放Pb的头节点（对应C++的delete Pb）Pb.clear()  # 清空Pb列表，标记为已释放def SubtractPolyn(Pa: list[PNode], Pb: list[PNode]) -> None:"""多项式减法：Pa = Pa - Pb（对应C++的SubtractPolyn）原理：创建Pb的相反数多项式，调用加法实现减法（Pa + (-Pb)）参数：Pa（被减多项式头节点列表）、Pb（减多项式头节点列表）"""# 1. 创建Pb的相反数多项式（对应C++的Polynomial negPb = new PNode）negPb = []  # 存储相反数多项式的头节点CreatePolyn(negPb, 0)  # 创建空多项式（仅头节点）negPb_head = negPb[0]p = Pb[0].next  # 遍历Pb的节点（对应C++的PNode* p = Pb->next）q = negPb_head  # 相反数多项式的当前节点（对应C++的PNode* q = negPb）while p is not None:# 系数取反，指数不变（对应C++的createNode(-p->coef, p->expn)）q.next = createNode(-p.coef, p.expn)q = q.nextp = p.next# 2. 调用加法实现减法（对应C++的AddPolyn(Pa, negPb)）AddPolyn(Pa, negPb)# 释放Pb的头节点（对应C++的delete Pb）Pb.clear()def MultiplyPolyn(Pa: list[PNode], Pb: list[PNode]) -> list[PNode]:"""多项式乘法：返回Pa * Pb的结果（对应C++的MultiplyPolyn）参数：Pa（第一个多项式头节点列表）、Pb（第二个多项式头节点列表）返回：存储乘积多项式头节点的列表"""# 初始化结果多项式（对应C++的Polynomial result = new PNode）result = []CreatePolyn(result, 0)  # 创建空多项式（仅头节点）result_head = result[0]# 处理空多项式（对应C++的if (!Pa->next || !Pb->next) return result）if Pa[0].next is None or Pb[0].next is None:return resultp1 = Pa[0].next  # 遍历Pa的节点（对应C++的PNode* p1 = Pa->next）while p1 is not None:p2 = Pb[0].next  # 遍历Pb的节点（对应C++的PNode* p2 = Pb->next）while p2 is not None:# 计算乘积项：系数相乘，指数相加（对应C++的coef = p1->coef * p2->coef）coef = p1.coef * p2.coefexpn = p1.expn + p2.expn# 插入结果多项式（对应C++的插入逻辑）pre = result_head  # 前驱节点q = result_head.next  # 当前节点while q is not None and q.expn < expn:pre = qq = q.nextif q is not None and q.expn == expn:# 合并同类项（对应C++的q->coef += coef）q.coef += coefif abs(q.coef) < 1e-6:# 系数为零，删除节点（对应C++的delete q）pre.next = q.nextelse:# 插入新节点（对应C++的createNode + 插入）newNode = createNode(coef, expn)newNode.next = qpre.next = newNodep2 = p2.nextp1 = p1.nextreturn resultdef getHighestTerm(P: list[PNode]) -> PNode:"""辅助函数：获取多项式最高次项节点（对应C++的getHighestTerm）参数：P（多项式头节点列表）返回：最高次项节点（None表示空多项式）原理：升序存储时，最后一个节点即为最高次项"""if P[0].next is None:return None  # 空多项式（对应C++的return NULL）p = P[0].next  # 首元节点（对应C++的PNode* p = P->next）while p.next is not None:p = p.nextreturn p  # 返回最后一个节点（最高次项）def DividePolyn(Pa: list[PNode], Pb: list[PNode], remainder: list[PNode]) -> list[PNode]:"""多项式除法：返回商多项式，余数通过remainder输出（对应C++的DividePolyn）数学关系：Pa = 商 × Pb + 余数（余数次数 < 除数次数）参数：Pa（被除数头节点列表）、Pb（除数头节点列表）、remainder（存储余数的列表）返回：存储商多项式头节点的列表"""# 初始化商多项式（对应C++的Polynomial quotient = new PNode）quotient = []CreatePolyn(quotient, 0)quotient_head = quotient[0]# 初始化余数多项式（对应C++的remainder = new PNode）CreatePolyn(remainder, 0)remainder_head = remainder[0]# 复制被除数到余数（对应C++的复制逻辑）p = Pa[0].next  # 遍历Pa的节点r = remainder_head  # 余数多项式的当前节点while p is not None:r.next = createNode(p.coef, p.expn)r = r.nextp = p.next# 检查除数是否为空（对应C++的if (!divisorHigh)）divisorHigh = getHighestTerm(Pb)if divisorHigh is None:print("除数不能为零多项式！")  # 对应C++的cerr输出return quotientdivisorExp = divisorHigh.expn    # 除数最高次项指数（对应C++的divisorExp）divisorCoef = divisorHigh.coef  # 除数最高次项系数（对应C++的divisorCoef）# 长除法核心循环（对应C++的while (true)）while True:remainderHigh = getHighestTerm(remainder)# 终止条件：余数为空或余数最高次项 < 除数最高次项（对应C++的break）if remainderHigh is None or remainderHigh.expn < divisorExp:break# 计算商项：余数最高次项 ÷ 除数最高次项（对应C++的qCoef和qExp）qCoef = remainderHigh.coef / divisorCoefqExp = remainderHigh.expn - divisorExp# 将商项插入商多项式（对应C++的插入逻辑）pre = quotient_headq = quotient_head.nextwhile q is not None and q.expn < qExp:pre = qq = q.nextqNode = createNode(qCoef, qExp)qNode.next = qpre.next = qNode# 计算：余数 = 余数 - (商项 × 除数)（对应C++的temp多项式）# 1. 创建商项×除数的临时多项式temp = []CreatePolyn(temp, 0)temp_head = temp[0]pb = Pb[0].nextwhile pb is not None:term_coef = qCoef * pb.coefterm_expn = qExp + pb.expnterm = createNode(term_coef, term_expn)# 头插法插入临时多项式（简化逻辑，后续取反不影响）term.next = temp_head.nexttemp_head.next = termpb = pb.next# 2. 创建temp的相反数多项式（对应C++的negTemp）negTemp = []CreatePolyn(negTemp, 0)negTemp_head = negTemp[0]t = temp[0].nextwhile t is not None:negTemp_head.next = createNode(-t.coef, t.expn)negTemp_head = negTemp_head.nextt = t.next# 3. 余数加上相反数（对应C++的AddPolyn(remainder, negTemp)）AddPolyn(remainder, negTemp)# 释放temp多项式（对应C++的DestroyPolyn(temp)）temp.clear()return quotientdef PrintPolyn(P: list[PNode]) -> None:"""多项式打印：降序输出（对应C++的PrintPolyn）参数：P（多项式头节点列表）说明：处理符号、系数简化（1/-1）、指数简化（1），符合数学表达式习惯"""if P[0].next is None:print("0")  # 空多项式输出0（对应C++的cout << "0" << endl）return# 收集所有非零项到列表（对应C++的pair数组）terms = []p = P[0].nextwhile p is not None:if abs(p.coef) > 1e-6:  # 过滤系数为零的项terms.append((p.coef, p.expn))p = p.next# 按指数降序排序（对应C++的逆序遍历数组）terms.sort(key=lambda x: x[1], reverse=True)first = True  # 标记是否为第一项（处理符号）for coef, expn in terms:abs_coef = abs(coef)# 1. 处理符号（对应C++的符号逻辑）if first:if coef < 0:print("-", end="")  # 首项负系数输出"-"first = Falseelse:if coef > 0:print(" + ", end="")  # 中间项正系数输出"+"else:print(" - ", end="")  # 中间项负系数输出"-"# 2. 处理系数（简化1/-1，对应C++的系数逻辑）if abs_coef != 1 or expn == 0:# 系数非1/-1 或 常数项（指数0），输出系数# 整数系数简化为整数格式（如2.0→2）if abs(abs_coef - round(abs_coef)) < 1e-6:print(int(abs_coef), end="")else:print(abs_coef, end="")# 3. 处理指数（简化x^1→x，对应C++的指数逻辑）if expn > 0:print("x", end="")if expn != 1:print(f"^{expn}", end="")print()  # 换行（对应C++的cout << endl）def DestroyPolyn(P: list[PNode]) -> None:"""多项式销毁：释放内存（对应C++的DestroyPolyn）参数：P（多项式头节点列表）说明：Python无需手动删除，清空列表标记为已释放即可"""P.clear()  # 清空列表，节点由垃圾回收自动回收def CopyPolyn(P: list[PNode]) -> list[PNode]:"""多项式复制：深拷贝（对应C++的CopyPolyn）参数：P（原多项式头节点列表）返回：新多项式头节点列表（与原多项式独立）"""copy = []  # 新多项式的头节点列表CreatePolyn(copy, 0)  # 创建空多项式（仅头节点）copy_head = copy[0]p = P[0].next  # 遍历原多项式的节点q = copy_head  # 新多项式的当前节点while p is not None:# 复制每个节点（对应C++的createNode(p->coef, p->expn)）q.next = createNode(p.coef, p.expn)q = q.nextp = p.nextreturn copydef main() -> None:"""主函数：模拟C++的main，实现多项式四则运算交互"""# 初始化多项式（对应C++的Polynomial Pa = NULL, Pb = NULL...）Pa = []Pb = []remainder = []# ===== 创建多项式Pa（对应C++的CreatePolyn(Pa, n1)）=====print("===== 创建多项式 Pa =====")while True:try:n1 = int(input("请输入Pa的项数："))if n1 >= 0:breakprint("项数不能为负数，请重新输入！")except ValueError:print("输入无效，请输入非负整数！")CreatePolyn(Pa, n1)print("Pa = ", end="")PrintPolyn(Pa)# ===== 创建多项式Pb（对应C++的CreatePolyn(Pb, n2)）=====print("\n===== 创建多项式 Pb =====")while True:try:n2 = int(input("请输入Pb的项数："))if n2 >= 0:breakprint("项数不能为负数，请重新输入！")except ValueError:print("输入无效，请输入非负整数！")CreatePolyn(Pb, n2)print("Pb = ", end="")PrintPolyn(Pb)# ===== 加法运算（对应C++的AddPolyn(PaAdd, PbAdd)）=====print("\n===== 执行加法：Pa + Pb =====")PaAdd = CopyPolyn(Pa)PbAdd = CopyPolyn(Pb)AddPolyn(PaAdd, PbAdd)print("Pa + Pb = ", end="")PrintPolyn(PaAdd)DestroyPolyn(PaAdd)  # 释放加法临时多项式# ===== 减法运算（对应C++的SubtractPolyn(PaSub, PbSub)）=====print("\n===== 执行减法：Pa - Pb =====")PaSub = CopyPolyn(Pa)PbSub = CopyPolyn(Pb)SubtractPolyn(PaSub, PbSub)print("Pa - Pb = ", end="")PrintPolyn(PaSub)DestroyPolyn(PaSub)  # 释放减法临时多项式# ===== 乘法运算（对应C++的MultiplyPolyn(Pa, Pb)）=====print("\n===== 执行乘法：Pa * Pb =====")product = MultiplyPolyn(Pa, Pb)print("Pa * Pb = ", end="")PrintPolyn(product)# ===== 除法运算（对应C++的DividePolyn(PaDiv, PbDiv, remainder)）=====print("\n===== 执行除法：Pa / Pb =====")PaDiv = CopyPolyn(Pa)PbDiv = CopyPolyn(Pb)quotient = DividePolyn(PaDiv, PbDiv, remainder)print("商 = ", end="")PrintPolyn(quotient)print("余数 = ", end="")PrintPolyn(remainder)# ===== 释放内存（对应C++的DestroyPolyn）=====DestroyPolyn(Pa)DestroyPolyn(Pb)DestroyPolyn(product)DestroyPolyn(quotient)DestroyPolyn(remainder)DestroyPolyn(PaDiv)DestroyPolyn(PbDiv)if __name__ == "__main__":main()

程序运行结果如下：

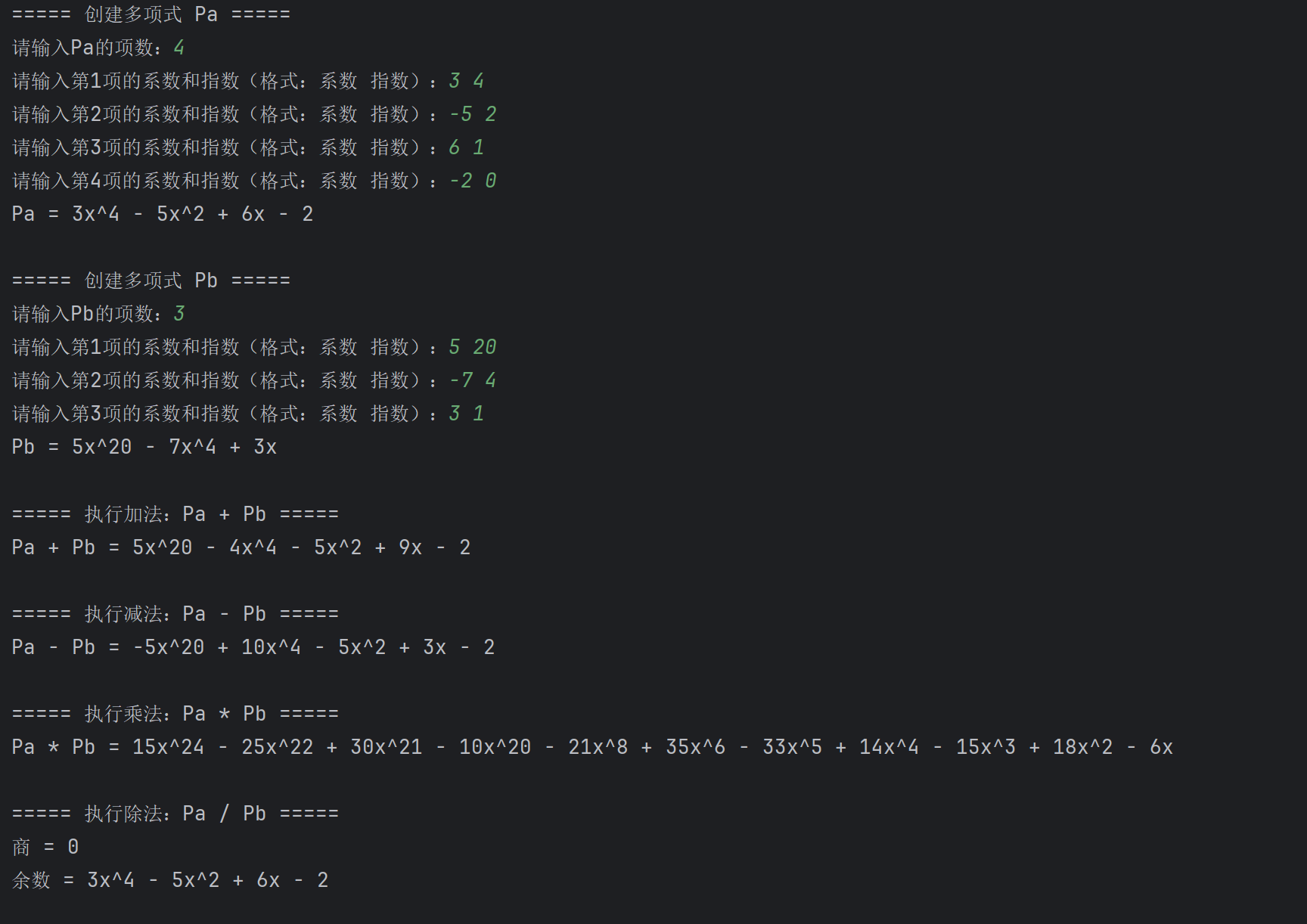
（三）Java代码如下：

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
import java.util.InputMismatchException;/*** 多项式节点类（对应C++的struct PNode）* 存储多项式的一项：系数、指数、下一项引用*/
class PNode {float coef;   // 系数（对应C++的float）int expn;     // 指数（对应C++的int）PNode next;   // 下一项引用（对应C++的PNode*）// 构造方法（对应C++的createNode函数）public PNode(float coef, int expn) {this.coef = coef;this.expn = expn;this.next = null;}
}/*** 多项式除法结果封装类（Java无引用传递，用类存储商和余数）*/
class PolynomialResult {PNode quotient;  // 商多项式头节点PNode remainder; // 余多项式头节点public PolynomialResult(PNode quotient, PNode remainder) {this.quotient = quotient;this.remainder = remainder;}
}/*** 多项式项封装类（用于打印时排序和格式化）*/
class Term {float coef;int expn;public Term(float coef, int expn) {this.coef = coef;this.expn = expn;}
}/*** 多项式四则运算主类（对应C++的全局函数和main）*/
public class PolynomialCalculator {/*** 1. 创建多项式（对应C++的CreatePolyn）* 功能：按指数升序插入项，自动合并同类项* @param scanner 输入扫描器（处理用户输入）* @param n 多项式项数* @return 多项式头节点（头节点不存储有效项，仅用于统一操作）*/public static PNode createPolyn(Scanner scanner, int n) {// 头节点：expn=-1（无意义），coef=0（占位）PNode head = new PNode(0.0f, -1);PNode pre = head; // 前驱节点（用于插入定位）for (int i = 1; i <= n; i++) {float coef = 0.0f;int expn = 0;boolean inputValid = false;// 处理输入格式错误，直到输入正确while (!inputValid) {System.out.printf("请输入第%d项的系数和指数（格式：系数 指数）：", i);try {coef = scanner.nextFloat();expn = scanner.nextInt();inputValid = true;} catch (InputMismatchException e) {System.out.println("输入格式错误！请按「数字 数字」格式输入（例：3.5 2 或 -2 1）");scanner.next(); // 清除无效输入缓存}}PNode newNode = new PNode(coef, expn);PNode curr = head.next;pre = head;// 找到插入位置：保持指数升序while (curr != null && curr.expn < newNode.expn) {pre = curr;curr = curr.next;}// 合并同类项（指数相等时）if (curr != null && curr.expn == newNode.expn) {curr.coef += newNode.coef;// 系数接近0（浮点数精度），删除该节点if (Math.abs(curr.coef) < 1e-6) {pre.next = curr.next;}} else {// 插入新节点到pre和curr之间newNode.next = curr;pre.next = newNode;}}return head;}/*** 2. 多项式加法（对应C++的AddPolyn）* 功能：Pa = Pa + Pb，结果存储在Pa中，Pb后续由GC自动回收* @param paHead Pa的头节点* @param pbHead Pb的头节点* @return 加法结果的头节点（即Pa）*/public static PNode addPolyn(PNode paHead, PNode pbHead) {PNode p1 = paHead.next; // Pa的有效项（首元节点）PNode p2 = pbHead.next; // Pb的有效项（首元节点）PNode p3 = paHead;      // 结果多项式的尾节点（初始为Pa头节点）while (p1 != null && p2 != null) {if (p1.expn == p2.expn) {// 同类项系数相加float sumCoef = p1.coef + p2.coef;if (Math.abs(sumCoef) > 1e-6) {p1.coef = sumCoef;p3.next = p1;p3 = p1;p1 = p1.next;// Pb当前项处理（Java无需手动删除）p2 = p2.next;} else {// 系数和为0，删除Pa和Pb的当前项PNode temp1 = p1;p1 = p1.next;temp1.next = null; // 断开引用，便于GC回收PNode temp2 = p2;p2 = p2.next;temp2.next = null;}} else if (p1.expn < p2.expn) {// Pa当前项指数更小，加入结果p3.next = p1;p3 = p1;p1 = p1.next;} else {// Pb当前项指数更小，加入结果p3.next = p2;p3 = p2;p2 = p2.next;}}// 处理剩余未遍历的项（直接链接）p3.next = (p1 != null) ? p1 : p2;return paHead;}/*** 3. 多项式减法（对应C++的SubtractPolyn）* 原理：Pa - Pb = Pa + (-Pb)（创建Pb的相反数多项式，再调用加法）* @param paHead 被减多项式头节点* @param pbHead 减多项式头节点* @return 减法结果的头节点（即Pa）*/public static PNode subtractPolyn(PNode paHead, PNode pbHead) {// 1. 创建Pb的相反数多项式（所有系数取反）PNode negPbHead = new PNode(0.0f, -1);PNode negPbCurr = negPbHead;PNode pbCurr = pbHead.next;while (pbCurr != null) {PNode newNode = new PNode(-pbCurr.coef, pbCurr.expn);negPbCurr.next = newNode;negPbCurr = newNode;pbCurr = pbCurr.next;}// 2. 调用加法实现减法return addPolyn(paHead, negPbHead);}/*** 4. 多项式乘法（对应C++的MultiplyPolyn）* 原理：双重循环遍历两项乘积，合并同类项后返回结果* @param paHead 第一个多项式头节点* @param pbHead 第二个多项式头节点* @return 乘积多项式的头节点*/public static PNode multiplyPolyn(PNode paHead, PNode pbHead) {PNode resultHead = new PNode(0.0f, -1); // 结果头节点// 空多项式检查（任一为空，结果为空）if (paHead.next == null || pbHead.next == null) {return resultHead;}PNode p1 = paHead.next; // 遍历Pa的项while (p1 != null) {PNode p2 = pbHead.next; // 遍历Pb的项while (p2 != null) {// 计算乘积项：系数相乘，指数相加float prodCoef = p1.coef * p2.coef;int prodExpn = p1.expn + p2.expn;PNode newNode = new PNode(prodCoef, prodExpn);PNode pre = resultHead;PNode curr = resultHead.next;// 找到插入位置（保持指数升序）while (curr != null && curr.expn < prodExpn) {pre = curr;curr = curr.next;}// 合并同类项if (curr != null && curr.expn == prodExpn) {curr.coef += prodCoef;if (Math.abs(curr.coef) < 1e-6) {pre.next = curr.next; // 系数为0，删除节点}} else {// 插入新节点newNode.next = curr;pre.next = newNode;}p2 = p2.next;}p1 = p1.next;}return resultHead;}/*** 辅助函数：获取多项式最高次项（对应C++的getHighestTerm）* 原理：升序存储时，最后一个节点即为最高次项* @param head 多项式头节点* @return 最高次项节点（null表示空多项式）*/public static PNode getHighestTerm(PNode head) {if (head.next == null) {return null;}PNode curr = head.next;while (curr.next != null) {curr = curr.next;}return curr;}/*** 5. 多项式除法（对应C++的DividePolyn）* 原理：长除法，反复用余数最高次项÷除数最高次项，直到余数次数<除数次数* @param paHead 被除数头节点* @param pbHead 除数头节点* @return 包含商和余数的PolynomialResult对象*/public static PolynomialResult dividePolyn(PNode paHead, PNode pbHead) {// 初始化商和余数的头节点PNode quotientHead = new PNode(0.0f, -1);PNode remainderHead = new PNode(0.0f, -1);// 1. 复制被除数到余数（避免修改原Pa）PNode paCurr = paHead.next;PNode remainderCurr = remainderHead;while (paCurr != null) {PNode newNode = new PNode(paCurr.coef, paCurr.expn);remainderCurr.next = newNode;remainderCurr = newNode;paCurr = paCurr.next;}// 2. 检查除数是否为空（零多项式）PNode divisorHigh = getHighestTerm(pbHead);if (divisorHigh == null) {System.out.println("错误：除数不能为零多项式！");return new PolynomialResult(quotientHead, remainderHead);}int divisorExp = divisorHigh.expn;    // 除数最高次项指数float divisorCoef = divisorHigh.coef; // 除数最高次项系数// 3. 长除法核心循环while (true) {PNode remainderHigh = getHighestTerm(remainderHead);// 终止条件：余数为空 或 余数最高次项 < 除数最高次项if (remainderHigh == null || remainderHigh.expn < divisorExp) {break;}// 计算商项：余数最高次项 ÷ 除数最高次项float qCoef = remainderHigh.coef / divisorCoef;int qExp = remainderHigh.expn - divisorExp;PNode qNode = new PNode(qCoef, qExp);// 插入商多项式（保持指数升序）PNode preQ = quotientHead;PNode currQ = quotientHead.next;while (currQ != null && currQ.expn < qExp) {preQ = currQ;currQ = currQ.next;}qNode.next = currQ;preQ.next = qNode;// 计算：余数 = 余数 - (商项 × 除数)// 步骤1：计算商项×除数的临时多项式PNode tempHead = new PNode(0.0f, -1);PNode tempCurr = tempHead;PNode pbCurr = pbHead.next;while (pbCurr != null) {float tempCoef = qCoef * pbCurr.coef;int tempExp = qExp + pbCurr.expn;tempCurr.next = new PNode(tempCoef, tempExp);tempCurr = tempCurr.next;pbCurr = pbCurr.next;}// 步骤2：计算临时多项式的相反数（用于减法）PNode negTempHead = new PNode(0.0f, -1);PNode negTempCurr = negTempHead;PNode tempCurr2 = tempHead.next;while (tempCurr2 != null) {negTempCurr.next = new PNode(-tempCurr2.coef, tempCurr2.expn);negTempCurr = negTempCurr.next;tempCurr2 = tempCurr2.next;}// 步骤3：余数 += 相反数（即余数 -= 临时多项式）addPolyn(remainderHead, negTempHead);}return new PolynomialResult(quotientHead, remainderHead);}/*** 6. 复制多项式（对应C++的CopyPolyn）* 功能：深拷贝多项式，避免原多项式被修改* @param head 原多项式头节点* @return 新多项式头节点*/public static PNode copyPolyn(PNode head) {PNode copyHead = new PNode(0.0f, -1);PNode copyCurr = copyHead;PNode curr = head.next;while (curr != null) {PNode newNode = new PNode(curr.coef, curr.expn);copyCurr.next = newNode;copyCurr = newNode;curr = curr.next;}return copyHead;}/*** 7. 打印多项式（对应C++的PrintPolyn）* 功能：降序输出，简化系数（1/-1）和指数（1），符合数学表达式习惯* @param head 多项式头节点* @param polyName 多项式名称（用于输出提示）*/public static void printPolyn(PNode head, String polyName) {List<Term> terms = new ArrayList<>();PNode curr = head.next;// 收集所有有效项（过滤系数为0的项）while (curr != null) {if (Math.abs(curr.coef) > 1e-6) {terms.add(new Term(curr.coef, curr.expn));}curr = curr.next;}// 空多项式处理if (terms.isEmpty()) {System.out.printf("%s = 0%n", polyName);return;}// 按指数降序排序（升序存储→需逆序）Collections.sort(terms, (t1, t2) -> Integer.compare(t2.expn, t1.expn));StringBuilder sb = new StringBuilder();boolean isFirstTerm = true; // 标记首项（处理符号）for (Term term : terms) {float coef = term.coef;int expn = term.expn;float absCoef = Math.abs(coef);// 1. 处理符号if (isFirstTerm) {if (coef < 0) {sb.append("-"); // 首项负系数显式加"-"}isFirstTerm = false;} else {if (coef > 0) {sb.append(" + "); // 中间项正系数加"+"} else {sb.append(" - "); // 中间项负系数加"-"}}// 2. 处理系数（简化1/-1，常数项必显式）if (absCoef != 1 || expn == 0) {// 整数系数简化为整数（如2.0→2）if (Math.abs(absCoef - Math.round(absCoef)) < 1e-6) {sb.append((int) absCoef);} else {sb.append(absCoef);}}// 3. 处理指数（简化x^1→x）if (expn > 0) {sb.append("x");if (expn != 1) {sb.append("^").append(expn);}}}System.out.printf("%s = %s%n", polyName, sb.toString());}/*** 辅助函数：获取有效项数（非负整数，处理输入错误）* @param scanner 输入扫描器* @param polyName 多项式名称（用于提示）* @return 非负整数项数*/public static int getValidTermCount(Scanner scanner, String polyName) {int count = 0;boolean valid = false;while (!valid) {System.out.printf("请输入%s的项数：", polyName);try {count = scanner.nextInt();if (count >= 0) {valid = true;} else {System.out.println("项数不能为负数，请重新输入！");}} catch (InputMismatchException e) {System.out.println("输入无效，请输入非负整数！");scanner.next(); // 清除无效输入缓存}}return count;}/*** 主函数（对应C++的main）：交互执行多项式四则运算*/public static void main(String[] args) {Scanner scanner = new Scanner(System.in);// 1. 创建多项式PaSystem.out.println("===== 创建多项式 Pa =====");int n1 = getValidTermCount(scanner, "Pa");PNode Pa = createPolyn(scanner, n1);printPolyn(Pa, "Pa");// 2. 创建多项式PbSystem.out.println("\n===== 创建多项式 Pb =====");int n2 = getValidTermCount(scanner, "Pb");PNode Pb = createPolyn(scanner, n2);printPolyn(Pb, "Pb");// 3. 加法运算System.out.println("\n===== 执行加法：Pa + Pb =====");PNode PaAdd = copyPolyn(Pa);PNode PbAdd = copyPolyn(Pb);PNode addResult = addPolyn(PaAdd, PbAdd);printPolyn(addResult, "Pa + Pb");// 4. 减法运算System.out.println("\n===== 执行减法：Pa - Pb =====");PNode PaSub = copyPolyn(Pa);PNode PbSub = copyPolyn(Pb);PNode subResult = subtractPolyn(PaSub, PbSub);printPolyn(subResult, "Pa - Pb");// 5. 乘法运算System.out.println("\n===== 执行乘法：Pa * Pb =====");PNode mulResult = multiplyPolyn(Pa, Pb);printPolyn(mulResult, "Pa * Pb");// 6. 除法运算System.out.println("\n===== 执行除法：Pa / Pb =====");PNode PaDiv = copyPolyn(Pa);PNode PbDiv = copyPolyn(Pb);PolynomialResult divResult = dividePolyn(PaDiv, PbDiv);printPolyn(divResult.quotient, "商");printPolyn(divResult.remainder, "余数");scanner.close();}
}

程序运行结果如下：