当前位置：首页 > news >正文

YOLO入门教程（番外）：计算机视觉数学、编程基础

news 2025/9/29 6:39:26

介绍计算机视觉学习中会用到的数学和编程基础知识，为后续学习做准备。我看了一下后面的内容，这特么要补充学习的概念太多了。慢慢来吧！！！

学习资料：《基于深度学习的目标检测原理与应用》
作者：翟中华孙云龙陆澍旸编著

1 向量、矩阵和卷积

1.1 向量

由多个数X1，X2，…，Xn组成的有序数组，称为向量。向量在计算机视觉中可以表示坐标系上的点，如平面上的点(x，y)、三维中的点(x，y，z)。

向量的常用操作有向量的点积(Dot Product)和向量的叉积(Cross Product)。

从代数意义上看，向量的点积是对两个向量中的每组对应元素求乘积，再对所有积求和；从几何意义上看，向量的点积可计算两个向量之间的角度，是一个向量在另一个向量方向上的投影。

向量的点积得到的结果是一个标量，如式(2-1)和式(2-2)所示。

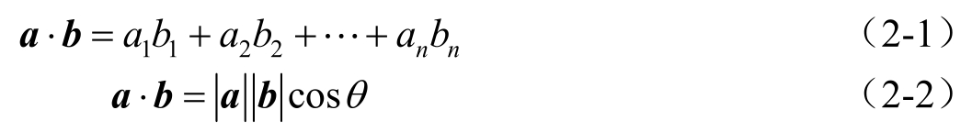
向量的叉积主要用在三维中，通过两个向量的叉积，生成第三个垂直于向量a和向量b构成的平面，其中i、j、k表示3个坐标轴的单位向量，从而可以在三维空间中建立x、y、z坐标系。向量的叉积仍为一个向量，也可称为法向量，如式(2-3)所示。

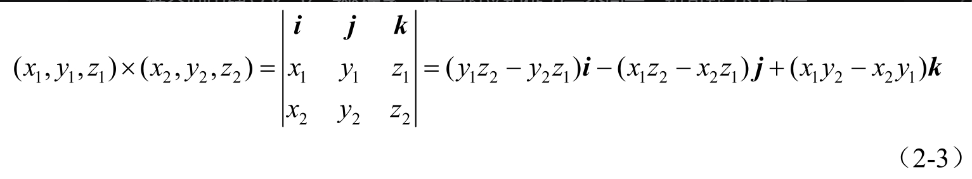
向量的范数(Norm)可以简单形象地理解为向量的长度，或者向量到零点的距离，或者相应的两个点之间的距离，表示为

1.2 矩阵

矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。

矩阵在计算机视觉中重要的应用是用来表达一幅图像，如图2-1-1所示。

矩阵的另一个重要运用是射影变化，将三维的点(x，y，z)转换成二维的点(x，y)，公式如下：

矩阵相乘的几何意义为两个线性变换的复合，公式如下：

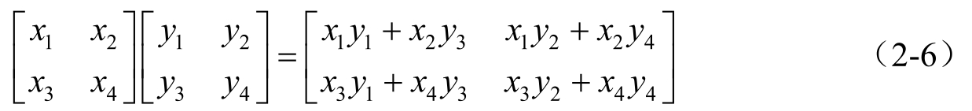
1.3 卷积

最开始，卷积(Convolution)是一个物理概念，出现在信号与线性系统中，对系统的单位响应与输入信号求卷积，以求得系统的输出信号。

后来，卷积被运用在数字图像处理中，与最初的原理相通，只是进一步将一维函数变成二维卷积核（卷积模板），在图像上滑动。每次滑动计算相当于矩阵的点积，直到把整幅图像遍历，如图2-1-2所示。

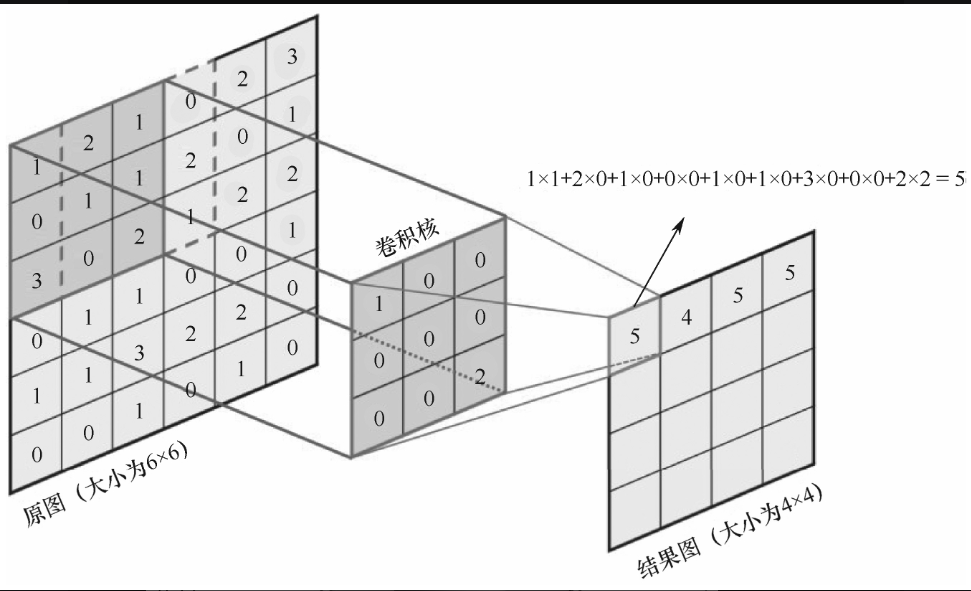
高斯卷积（高斯模糊，Gaussian Blur）是常用的卷积应用之一。

为了使图像没有突出的特征点，引入了模糊的概念。简易的模糊方法是选取每个像素周边像素的平均值。

我挺疑惑为甚需要模糊

用途类别	主要作用	实现原理与效果	典型示例
1. 降噪	减少图像中的随机噪声和微小的不规则瑕疵。	通过取目标像素周围邻域像素的平均值（或加权平均），使孤立的噪声点被“平滑”和“冲淡”，融入周边区域。	去除照片中的数码噪点，使画面更干净。
2. 预处理	为后续高级算法（如边缘检测、图像分割、目标识别）提供更干净、更稳定的输入。	消除过于细微的纹理和噪声的干扰，让算法能专注于宏观的、重要的结构特征，从而提升准确性和鲁棒性。	在检测物体轮廓前先进行模糊，可以得到更连贯、更少毛刺的边缘线。
3. 美学效果	模拟特定的光学效果或营造特殊的视觉氛围。	有选择地降低某些区域的清晰度，改变图像的视觉效果。	背景虚化（突出主体）、人像美肤（软化瑕疵）、动态模糊（增强速度感）。
4. 隐私保护	隐藏图像中的敏感个人信息。	对特定区域进行强烈模糊，使得细节信息无法被辨认。	模糊车牌、人脸、证件号码等。
核心思想	权衡（Trade-off）	以牺牲图像细节（分辨率）为代价，换取噪声减少、特征突出、稳定性提升等好处。	根据具体需求选择合适的模糊算法和强度。

高斯模糊不是简单选取平均值，而是用高斯分布与图像做卷积，换句话说，就是加权，即将某点的像素用周围点的加权来表示，距离该点距离越近的点权重越大，越远的点权重越小，从而减少“被平均”的偏误，

如图2-1-3所示。二维高斯函数表达式为

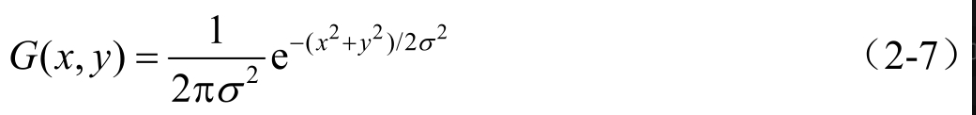
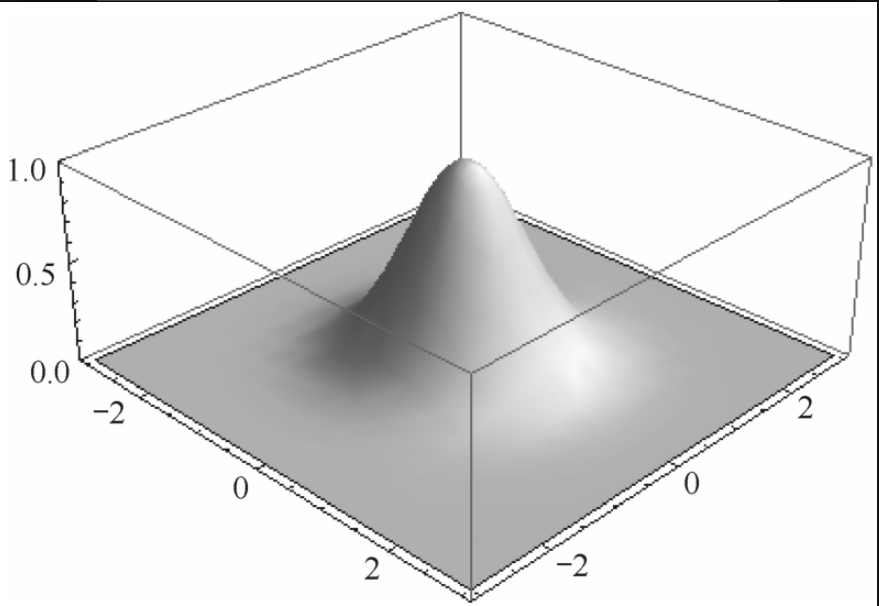
不同卷积会造成不同的效果。双边滤波(Bilateral Filter)更接近磨皮的效果，比原始图像更光滑；高斯滤波会模糊原始图像。

加入噪声后检测，双边滤波和高斯滤波基本可去除噪声。运用不同滤波的对比如图2-1-4所示。

卷积神经网络(Convolutional Neural Networks，CNN)与高斯卷积不同之处在于，其每层都运用多个卷积核。

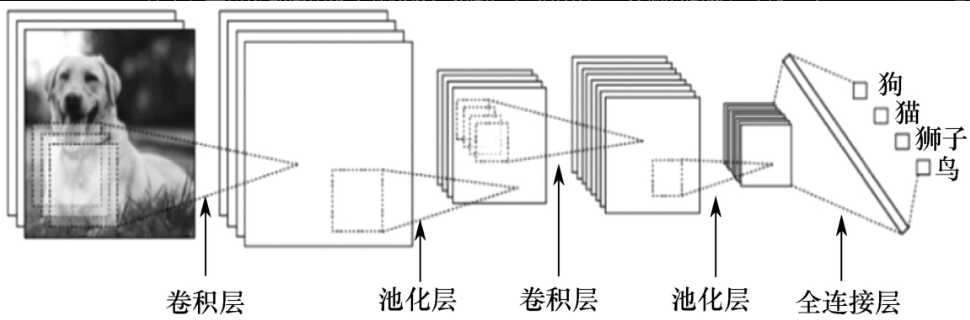
如图2-1-5所示，**一只狗的图像，经过一个卷积层，会输出多幅图像。**一般来说，运用3×3的卷积核即可生成多幅不同特征的图像。其好处是可以使用不同的卷积核学习不同的特征。

2 函数极值理论与非极大值抑制

在深度学习的建模与优化过程中，因为大多数需要解决的现实问题不像方程式一样有闭式解，所以需通过建立一个损失函数，使得模型的预测结果无限靠近真实值。

具体方法就是将损失函数的损失值尽可能降低，也就是求损失函数的极值。

在目标检测中预测网络通常会产生大量的预测候选框(Anchor Box/BoundingBox)，而且预选框的数量要远远大于被检测的目标数。这时需要用到非极大值抑制来消除掉不需要的候选框。

2.1 函数极值理论

为什么求函数的极值？深度学习、机器学习建模过程就是寻找一个最优解，达到最好的预测效果，简单来说，就是通过降低损失函数的损失来求得模型的最优参数。

如何求函数的最小值？一般就是求导数为零的点，但导数为零的点一定是极值点吗？不一定，当一阶导数为0时，可能是一条平行于x轴的直线，根本没有极大和极小的问题，因此，一阶导数为0是极值点的必要条件，而非充分条件。

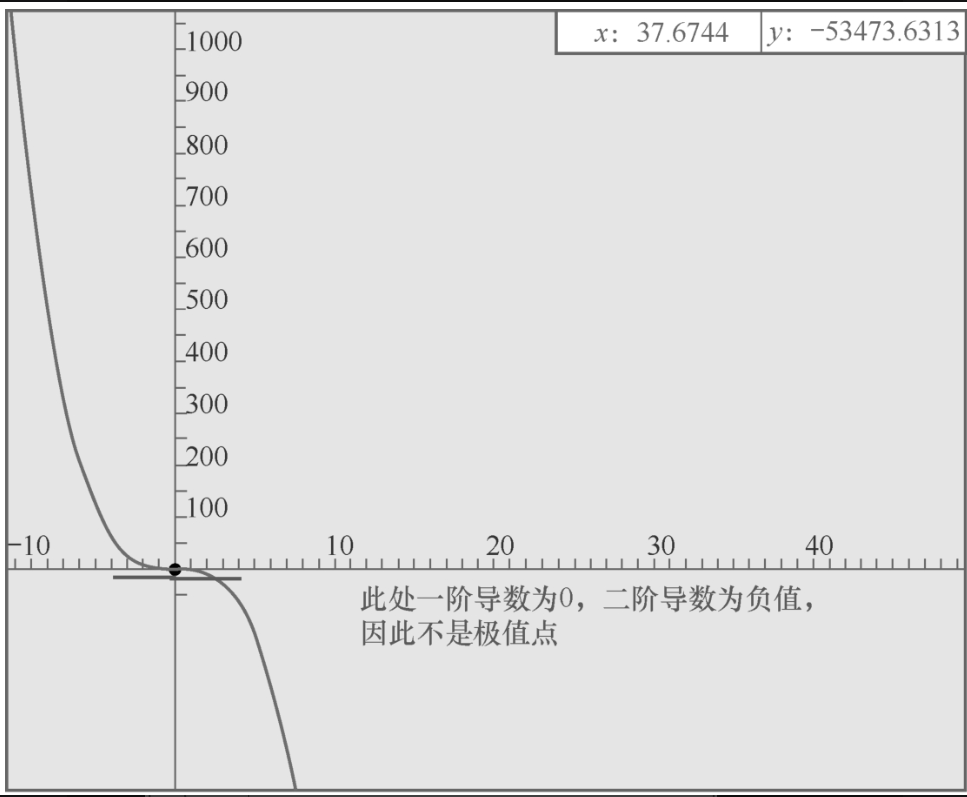
再如，f(x)=-x3的函数图像如图2-2-1所示，虽然在x=0处函数的一阶导数为0，但是x=0并不是函数的极值点。

如果是极值点，不是上凹，就是下凹。如果是上凹，则极值点处的二阶导数一定大于0，为极小值点；如果是下凹，则极值点处的二阶导数一定小于0，为极大值点。

在使用深度学习解决实际问题的过程中，很难找出与实际问题相吻合的函数，因此，使用梯度下降法使模型预测的结果不断靠近正确值。

所谓梯度，就是在多维坐标空间中，该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快、变化率最大（为该梯度的模）。

直观地理解，在图2-2-2中，起始点A到达最低点B最快捷的路径，就是沿着梯度方向下降，其函数表达式为f(x，y)=x2+y2，假设A点的坐标为(1，1)，则该点的梯度：

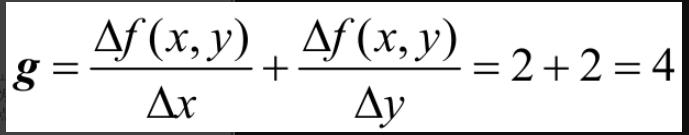
注意，梯度是一个向量，不是标量。

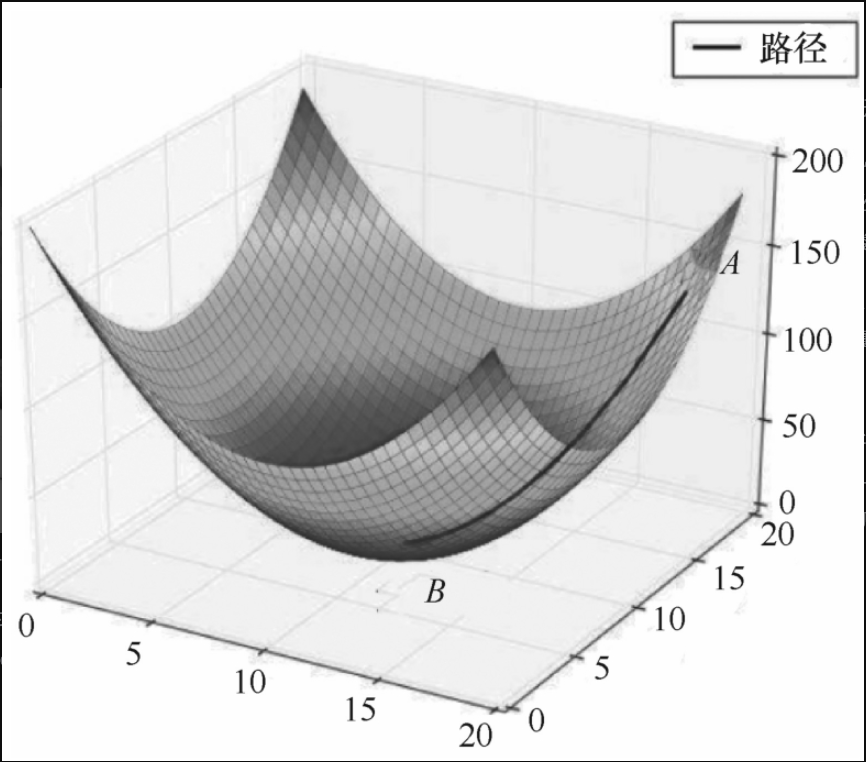
梯度下降更新参数w的公式为

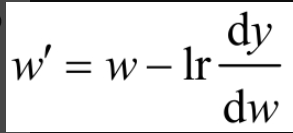
其中，w′是经过一轮更新得到的参数；lr是学习率(Learning Rate)；

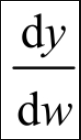
是损失函数的梯度。

假设损失函数是：

函数的图形如图2-2-3所示，相应的

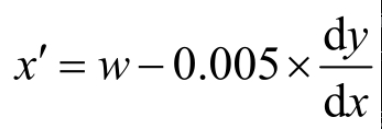
其中，0.005就是学习率，当x=3时，

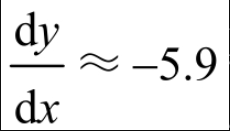
如果这里没有使用lr对x的更新进行约束，那么x′=3-(-5.9)=8.9，比以前更大，因此，用lr对参数更新进行约束，使参数逐步逼近极值点。

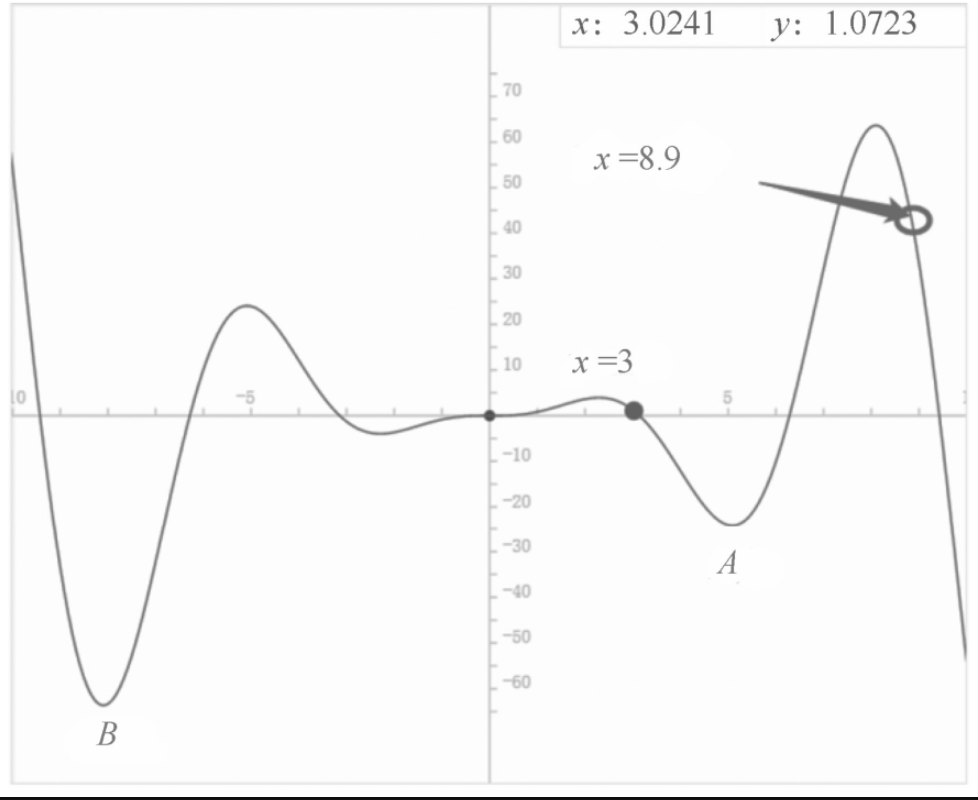
但是，从x=3出发求出的极值就在A点，显而易见，A点并不是在定义域内真正的极值点，而是一个局部最优点，真正的全局最优点在B点。

这就引出随机梯度下降法。随机梯度下降法，顾名思义，就是随机在坐标上选择多个起始点进行梯度下降，从而避免局部最优的问题。

如图2-2-3所示，对于函数f(x)=x2 sinx，x的定义域为(-10，10)，在定义域中随机取多个x进行梯度下降，最后就能找到全局最优点B点。

以上计算f(x)结果的过程是正向传播，利用计算结果对参数w进行更新的过程是反向传播，只不过在PyTorch或者TensorFlow等框架中，是通过神经网络进行的。

2.2 非极大值抑制

候选框是指候选出有可能存在物体的框。如图2-2-4所示，一张图中有众多候选框，狗的眼睛、鼻子甚至狗的整体，都属于单独的候选框。

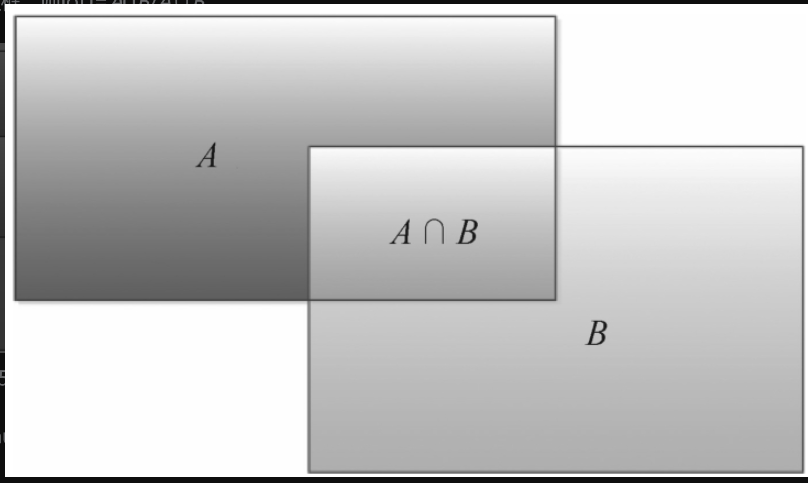
如何在众多候选框中挑出有用的候选框？这将涉及新的概念——交并比(IoU)。交并比是预测框与真值框的交集与并集的比值。

如图2-2-5所示，假设A是候选框，B是正确的真值框，则IoU=A∩B/A∪B。

通过非极大值抑制(Non-Maximum Suppression，NMS)剔除定位不太精确的框的过程如下。

输入：候选框B的列表、对应的置信度S和重叠阈值N。

输出：过滤后的候选框列表D。选择候选框的过程如图2-2-6所示。

(1)选择置信度（得分）最高的候选框，将其从B中移除，并将其添加到最终候选框列表D（最初D为空）中。
(2)将（置信度最高的候选框与所有候选框进行比较——计算该候选框与其他候选框的交并比。如果交并比大于阈值N，则从B中删除该候选框。为什么不删除小于阈值N的候选框？因为这些候选框虽然不是框住当前这个目标的好的候选框，但可能是框住其他目标的好的候选框，所以不能删除。
(3)再次从B剩余的候选框中取出具有最高置信度的候选框，将其从B中删除并添加到D中。
(4)再次计算B中的所有候选框与步骤(3)中选出的候选框的交并比，并剔除交并比高于阈值的框。重复这个过程，直到B中没有更多的候选框。

非极大值抑制代码如下。

import numpy as np# 定义候选框数组dets
# 每一行格式: [x1, y1, x2, y2, score]
# (x1, y1) 是边界框左上角的坐标
# (x2, y2) 是边界框右下角的坐标
# score     是该框内包含物体的置信度
dets = np.array([[83, 54, 165, 163, 0.8],  # 候选框1，置信度0.8（最高）[67, 48, 118, 132, 0.5],  # 候选框2，置信度0.5[91, 38, 192, 171, 0.6]   # 候选框3，置信度0.6
], dtype=np.float32)def nms(dets, thresh):"""非极大值抑制函数 (Non-Maximum Suppression, NMS)用于目标检测中，去除针对同一目标的重叠候选框，只保留最可信的一个。参数:dets (numpy.ndarray): 候选框数组，形状为(N, 5)，每行为[x1, y1, x2, y2, score]。thresh (float): 交并比阈值。重叠度高于此阈值的框将被抑制。返回:list: 经过筛选后，保留下来的候选框在原始dets数组中的索引列表。"""# 1. 从dets中提取所有坐标和置信度x1 = dets[:, 0]  # 所有框的左上角x坐标y1 = dets[:, 1]  # 所有框的左上角y坐标x2 = dets[:, 2]  # 所有框的右下角x坐标y2 = dets[:, 3]  # 所有框的右下角y坐标scores = dets[:, 4]  # 所有框的置信度分数# 2. 计算每个候选框的面积# 面积 = (x2 - x1 + 1) * (y2 - y1 + 1)# 这里+1是为了避免在计算IoU时，面积为0的情况（例如框只有一个像素点）。areas = (x2 - x1 + 1) * (y2 - y1 + 1)# 3. 对置信度分数进行降序排序，并获取排序后的索引(order)# argsort()默认返回升序的索引，[::-1]将其反转，变为降序。# 这样，order中的第一个索引就是分数最高的那个框的索引。order = scores.argsort()[::-1]print('按置信度降序排列的索引 order =', order)  # 示例输出: [0, 2, 1] (因为0.8>0.6>0.5)# 4. 初始化一个空列表，用于存放最终保留的框的索引keep = []# 5. 开始NMS核心循环，只要还有未处理的框就继续while order.size > 0:# 5.1 取出当前置信度最高的框（即order中的第一个索引）i = order[0]# 将这个框的索引添加到保留列表keep中keep.append(i)# 5.2 计算当前最高分框 `i` 与 order 中**所有其他剩余框**的交集坐标# order[1:] 是除了当前最高分框之外的所有框的索引# np.maximum 是逐元素比较取最大值，用于计算相交区域的左上角坐标(x1, y1)xx1 = np.maximum(x1[i], x1[order[1:]])yy1 = np.maximum(y1[i], y1[order[1:]])# np.minimum 用于计算相交区域的右下角坐标(x2, y2)xx2 = np.minimum(x2[i], x2[order[1:]])yy2 = np.minimum(y2[i], y2[order[1:]])# 5.3 计算交集区域的宽度、高度和面积# np.maximum(0.0, ...) 确保宽和高不为负。# 如果两个框不相交，则`xx2 - xx1 + 1`为负，经过max(0)处理后变为0。w = np.maximum(0.0, xx2 - xx1 + 1)h = np.maximum(0.0, yy2 - yy1 + 1)inter = w * h  # 交集面积# 5.4 计算交并比 (Intersection over Union, IoU)# IoU = 交集面积 / (并集面积)# 并集面积 = 面积i + 面积others - 交集面积ovr = inter / (areas[i] + areas[order[1:]] - inter)print(f'当前最高分框 {i} 与剩余框的IoU ovr = {ovr}')# 5.5 找出那些与当前框 `i` 重叠度**低于或等于**阈值的框的索引# np.where(condition)[0] 返回满足条件(condition)的元素的索引。# 这里条件是 ovr <= thresh，即找到所有与当前框不太重叠的框。# 这些框被认为是检测到了**不同目标**的框，所以需要保留下来进入下一轮循环。inds = np.where(ovr <= thresh)[0]print(f'与框 {i} 重叠度低于阈值 {thresh} 的框索引(在order[1:]中的位置) inds = {inds}')# 5.6 更新order数组，只保留那些与当前框 `i` 重叠度低的框# 因为inds是基于order[1:]的索引（即比当前order数组少了第一个元素），# 所以为了在原始order数组中定位这些框，需要 inds + 1。# 这样，order就变成了下一轮循环要处理的框的索引集合。order = order[inds + 1]print(f'下一轮待处理框 order = {order}\n')# 6. 循环结束，返回所有保留下来的框的索引return keep# 设置IoU阈值并调用NMS函数
iou_threshold = 0.3
result_indices = nms(dets, iou_threshold)# 打印最终结果
print("最终保留的框在原始dets中的索引:", result_indices)
print("经过NMS筛选后的框:")
print(dets[result_indices])

核心逻辑总结 (分步说明)

排序: 首先将所有候选框按置信度从高到低排序。我们总是优先处理最确信的检测结果。
选取与抑制:
- 选择置信度最高的框 B_max，并将其加入最终保留列表。
- 计算 B_max 与所有其他剩余框的交并比 (IoU)。
阈值判断:
- 如果某个框与 B_max 的 IoU 高于阈值 thresh，则认为它和 B_max 检测的是同一个目标，且由于它的置信度更低，因此应被抑制（丢弃）。
- 如果 IoU 低于或等于 阈值 thresh，则认为它检测的是另一个不同的目标，应被保留以进行后续处理。
迭代: 在剩余的（未被抑制的）框中重复步骤2和3，直到没有框剩下为止。