当前位置：首页 > news >正文

机器学习之逻辑回归（梯度下降,Z标准化,0-1归一化）

news 2025/9/29 6:32:19

一、什么是逻辑回归

逻辑回归也称作logistic回归分析，是一种由线性回归衍生出来的分析模型，属于机器学习中的监督学习。其推导过程与计算方式类似于回归的过程，但实际上主要是用来解决二分类问题（也可以解决多分类问题）。通过给定的n组数据（训练集）来训练模型，并在训练结束后对给定的一组或多组数据（测试集）进行分类。其中每一组数据都是由p 个指标构成。

逻辑回归所处理的数据

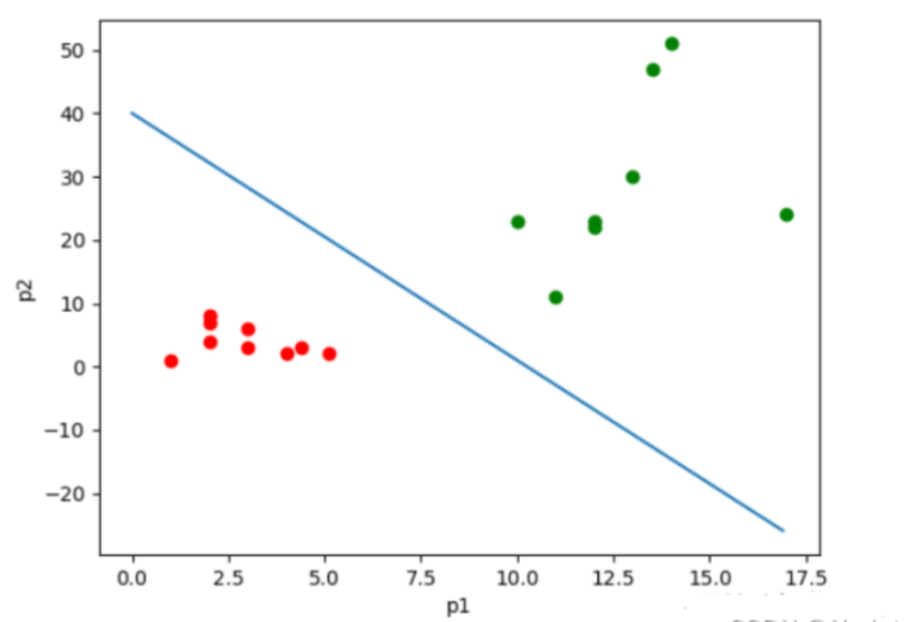
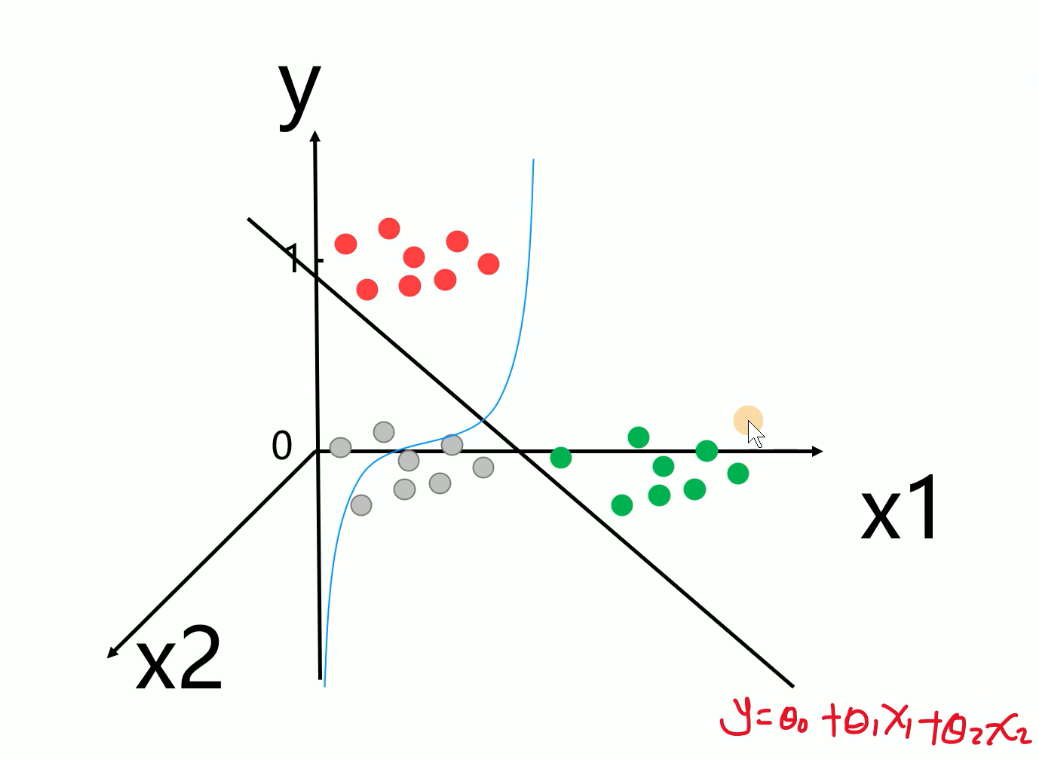
如果数据是有两个指标，可以用平面的点来表示数据，其中一个指标为x轴，另一个为y轴；如果数据有三个指标，可以用空间中的点表示数据；如果是p维的话(p>3)，就是p维空间中的点

逻辑回归的输⼊就是⼀个线性回归的结果。

二、引入sigomd函数

但这种函数一看就知道是一条斜线，难以达到我们想要进行二分类的效果0-1分类（分恶性与良性）取值，于是就有了采用Sigmoid函数

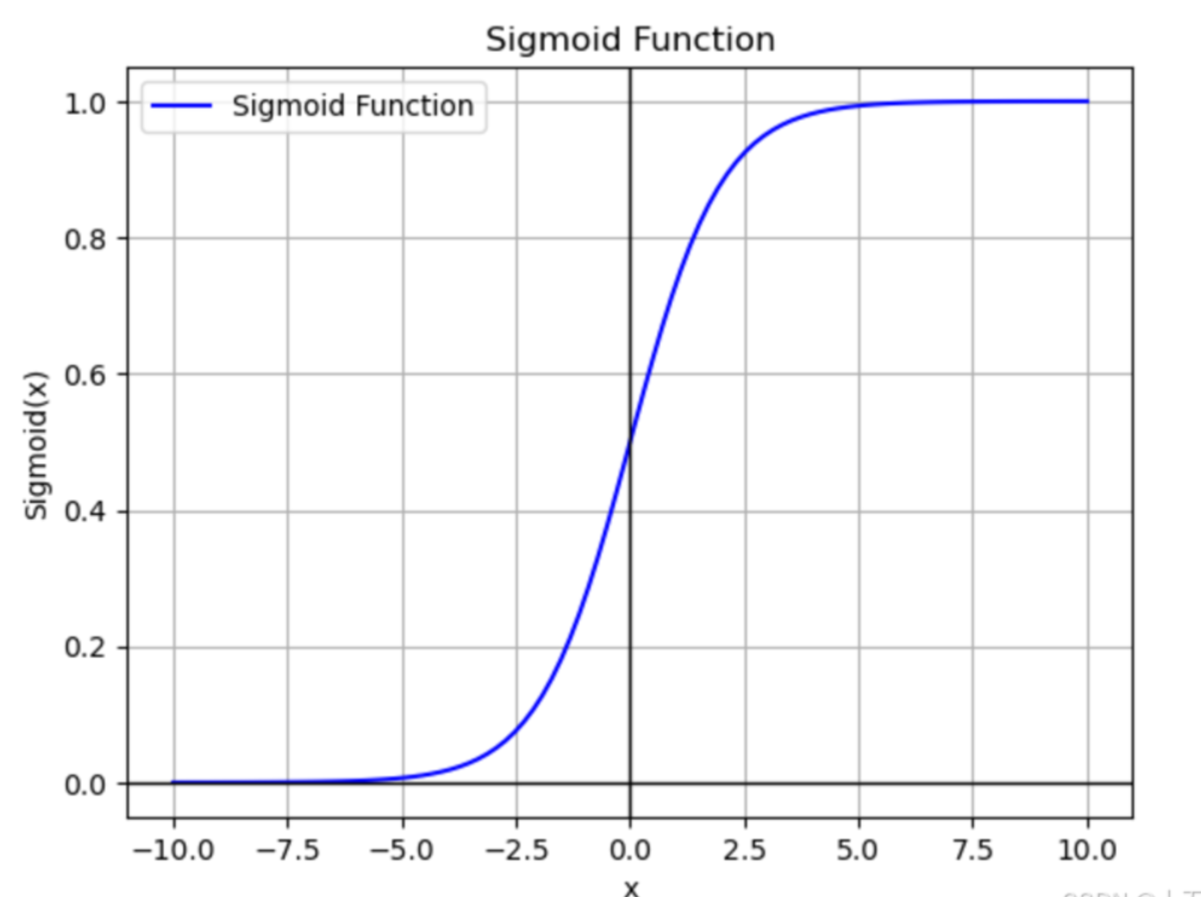
sigmoid函数公式

回归的结果输⼊到sigmoid函数当中（Z=h（w），将线性回归的结果带入）

输出结果：[0, 1]区间中的⼀个概率值，默认为0.5为阈值

对于二分类任务得出式子：

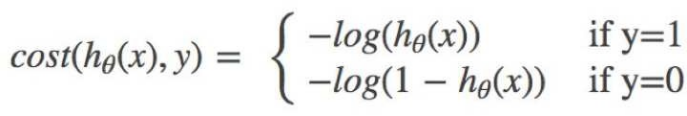
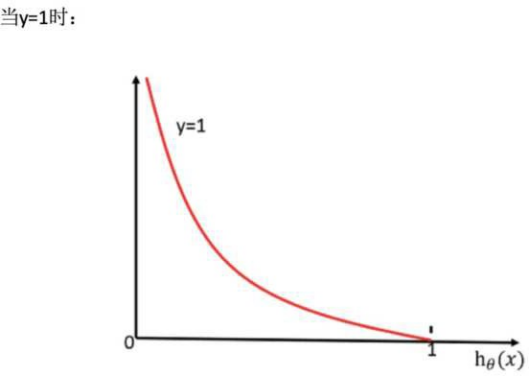
⽆论何时，我们都希望损失函数值，越⼩越好分情况讨论，对应的损失函数值：

⽆论何时，我们都希望损失函数值，越⼩越好

分情况讨论，对应的损失函数值：

当y=1时，我们希望hθ(x)值越⼤越好；

当y=0时，我们希望hθ(x)值越⼩越好

综合完整损失函数

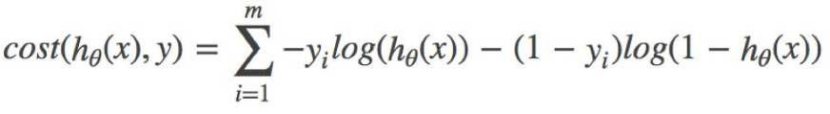
三、引入梯度下降法

梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

场景假设

梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处。

梯度下降（Gradient Descent）公式

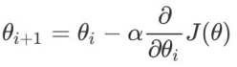
1、 α是什么含义？

α在梯度下降算法中被称作为学习率或者步⻓，意味着我们可以通过α来控制每⼀步⾛的距离

2、为什么梯度要乘以⼀个负号？

梯度前加⼀个负号，就意味着朝着梯度相反的⽅向前进！我们在前⽂提到，梯度的⽅向实际就是函数在此点上升最快的⽅向！⽽我们需要朝着下降最快的⽅向⾛，⾃然就是负的梯度的⽅向，所以此处需要加上负号

四、逻辑回归api介绍

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)

solver可选参数:{'liblinear', 'sag'（随机平均梯度下降）, 'saga','newton-cg'（基于牛顿法）}，默认: 'liblinear'；⽤于优化问题的算法基于坐标下降法。

penalty：正则化的种类，有L1和L2两种方法

C：正则化⼒度(惩罚因子),C越小正则化惩罚越强

max_iter:最大迭代次数

五、案例

寝室分类案例

import numpy as np
from sklearn.linear_model import LogisticRegression
data = np.loadtxt(r'F:\python-learn\datingTestSet2.txt')
# data_1 = data[data[:,3]==1]
# data_2 = data[data[:,3]==2]
# data_3 = data[data[:,3]==3]
X = data[:,:-1]
y = data[:,-1]
from  sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test =\train_test_split(X, y,test_size=0.3,random_state=100 )
lr = LogisticRegression(C=0.01)
lr.fit(x_train,y_train)
print("正确率：",lr.score(x_test,y_test))

train_target:所要划分的样本标签

test_size:样本占比，如果是整数的话就是样本的数量，如果是小数，就是占比。

random_state:是随机数的种子。随机数种子:其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。随机数和种子之间的关系遵从以下两个规则:种子不同，产生不同的随机数;种子相同，每次产生相同的随机数。

三条线X1，X2，X3值

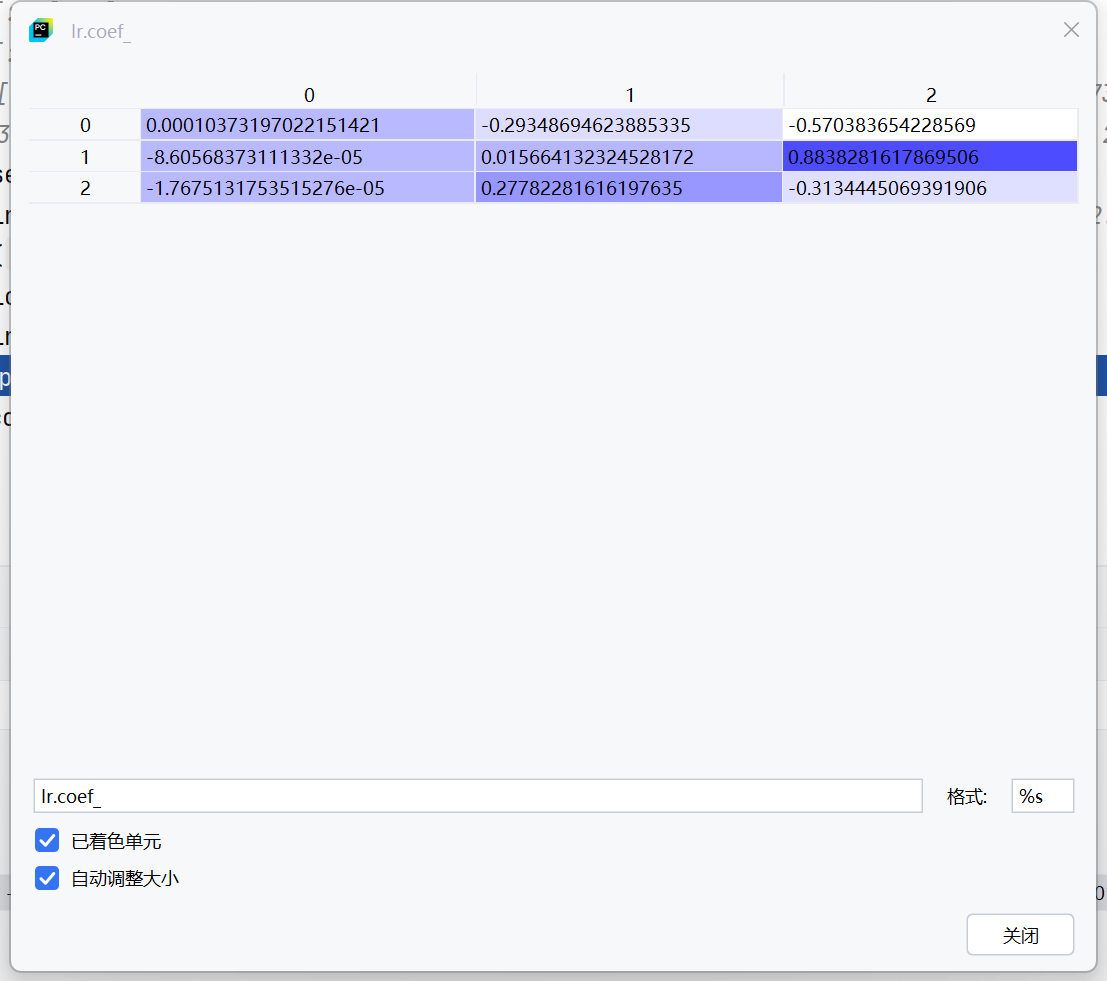
β0的三个值

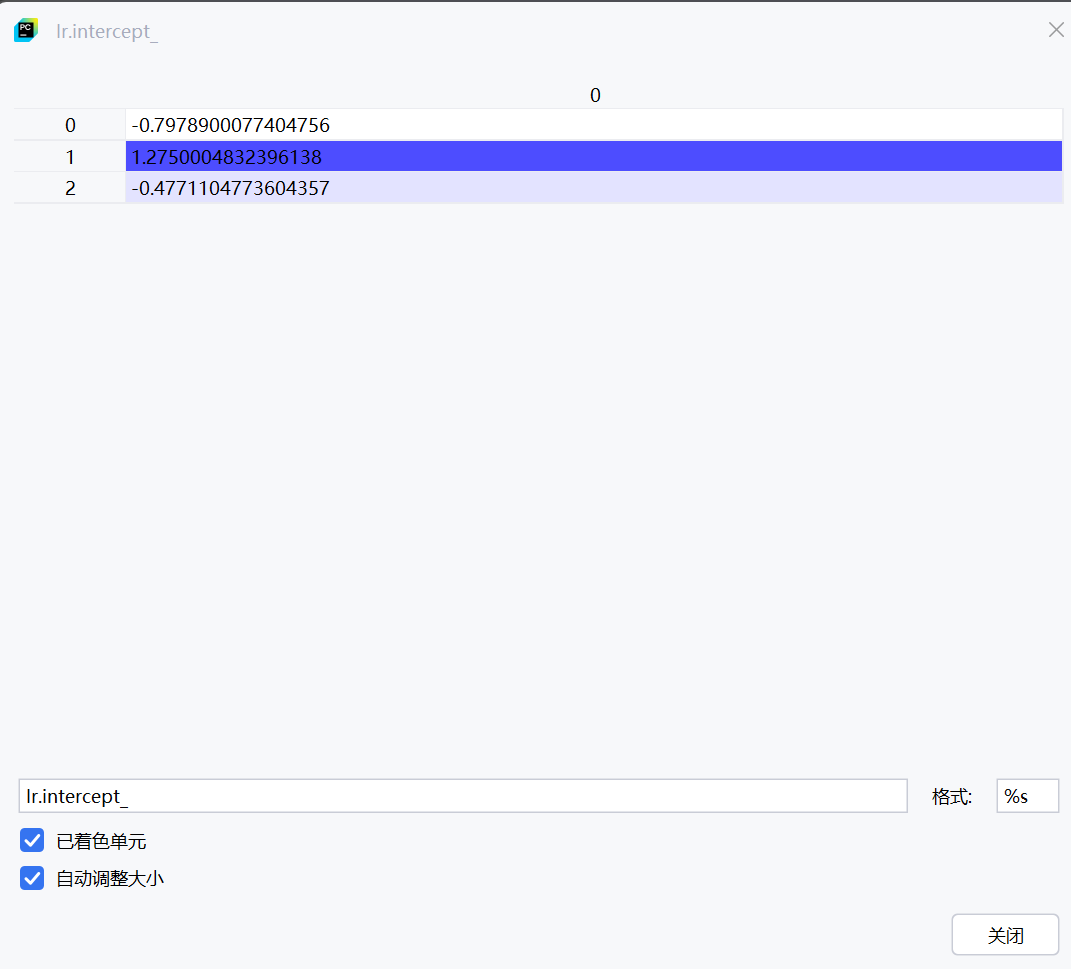
银行贷款案例

Z-Score标准化

其中：

$x$ 是原始数据，

$\mu$ 是数据的均值，

$\sigma$ 是数据的标准差，

$x^{'}$ 是归一化后的数据，具有零均值和单位标准差。

优点：不受极端值的影响，适合处理具有正态分布的数据。

缺点：如果数据分布不是高斯分布，效果可能较差；不能保证数据范围在 [0, 1] 之间。

例子：假设数据的均值为 200，标准差为 50，某个数据点为 300，计算 Z-score 归一化为：

$x^{'}=\frac{300-200}{50}=2$

0-1归一化

$x$ 是原始数据，

$x_{min}$ 是数据的最小值，

$x_{max}$ 是数据的最大值，

$x^{'}$ 是归一化后的数据，值域在[0，1]之间。
优点：保持数据间的比例关系，简单易行，适合有固定上下界的数据场景。

缺点：对极端值（outliers）敏感，如果数据中存在极端值，所有数据都可能被压缩到很小的区间。

例子：假设某个特征的数据范围为 [100, 500]，如果要将它归一化到 [0, 1]，对于某个数据点 200，则归一化计算为：

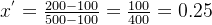
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_csv(r'F:\机器学习\逻辑回归\creditcard.csv')
from sklearn.preprocessing import StandardScaler#z标准换的函数
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data['Amount'].values.reshape(-1,1))
data = data.drop(['Time'],axis=1)#测除Time列的内容，axis为1表小列。
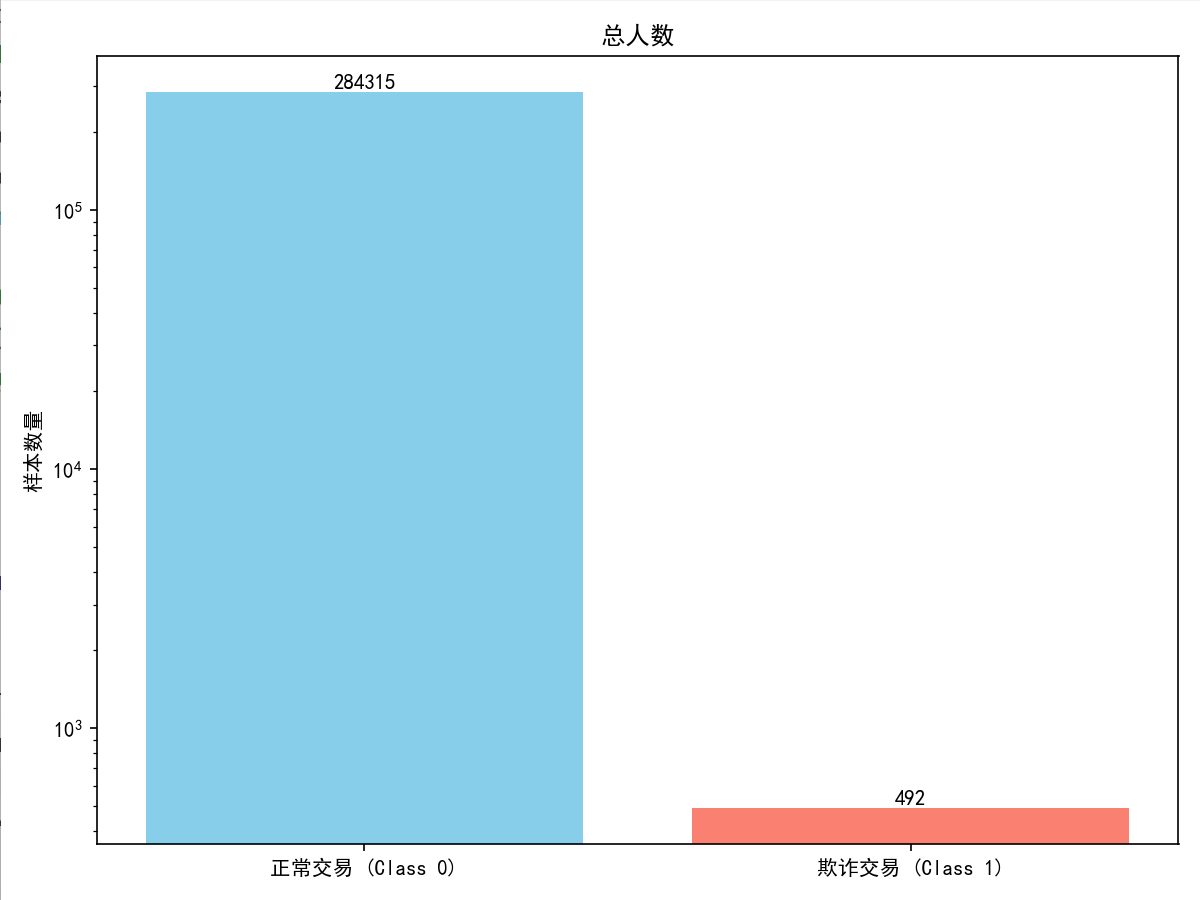
plt.figure(figsize=(8, 6))
class_counts = data['Class'].value_counts()
plt.bar(['正常交易 (Class 0)', '欺诈交易 (Class 1)'], class_counts.values,color=['skyblue', 'salmon'])
plt.ylabel('样本数量')
plt.title('总人数')
plt.yscale('log')  # 使用对数刻度，因为两类样本数量差异很大
for i, v in enumerate(class_counts.values):plt.text(i, v, str(v), ha='center', va='bottom')
plt.tight_layout()
plt.show()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = \train_test_split(data.drop(['Class'],axis=1),data['Class'],test_size=0.25,random_state=1000)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1)
lr.fit(x_train,y_train)
print("预测结果：",lr.predict_proba(x_test))
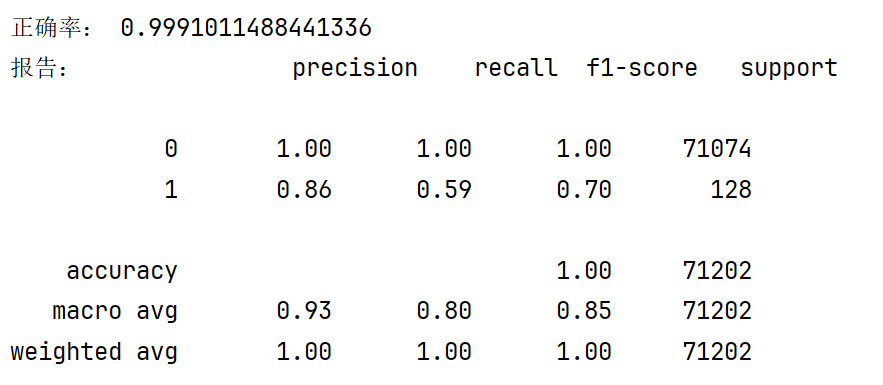
print("正确率：",lr.score(x_test,y_test))
from sklearn.metrics import classification_report
print("报告：",classification_report(y_test,lr.predict(x_test)))