基于神经网络的简单PID控制
PID(Proportional-Integral-Derivative,比例 - 积分 - 微分)控制算法是工业自动化领域应用最广泛的经典控制策略之一。通过对系统误差的 “比例调节”“积分补偿” 和 “微分预判”,实现对被控对象的精准、稳定控制,主要用于对驱动器的控制
点击下方链接获取源代码或者订购专栏私信获取!
基于神经网络的PID控制
一、PID 控制的核心思想
PID 控制的本质是基于 “误差” 进行闭环调节:通过传感器实时采集 “被控量”(实际值),与 “目标值”比较得到 “误差信号”(误差 = 目标值 - 实际值),再通过比例、积分、微分三个环节对误差进行处理,输出控制信号(控制量),最终使被控量趋近于目标值并保持稳定,并对控制量进行实时调整,直到误差值达到理想设定的范围,停止控制量的输出。
简单来说,PID 的核心逻辑是:
- 比例(P):“当下” 根据误差大小直接调节(误差越大,调节力度越强);
- 积分(I):“过去” 根据误差累积补偿(消除长期稳定后的微小误差,即 “静差”);
- 微分(D):“未来” 根据误差变化趋势预判(抑制被控量的超调,提升响应速度)。
二、PID 控制的数学模型与三个核心环节
PID 控制器的输出信号是比例、积分、微分三个环节输出的叠加,其连续时间域数学表达式为:
其中:
:t 时刻的误差信号(
,
为实际控制量,
为目标控制量);
:比例系数(核心调节参数,决定比例环节的力度);
:积分时间常数(反比于积分力度,
越小,积分作用越强);
:微分时间常数(正比于微分力度,
越大,微分作用越强)。
对上述公式进行展开得:
在这里将上述公式公式进行改写,令:
因此PID模型变为与Kp,Ki,Kd相关的关系式:
从公式来说,PID模型的控制量与Kp,Ki,Kd相关,只需要对应的调整此三个系数的大小,进而可以让控制量达到理想的状态。
三、神经网络优化PID
神经网络在处理非线性优化、预测分类有着很好的优势,只需要输入对应的神经元大小,即可输出对应的值,这就很适合我们的PID控制。
只需要把PID模型中对应的Kp、Ki、Kd当做输出层神经元,将对应的输入神经元为误差、误差变化率、控制量!
将每次所得的PID控制系数,带入PID模型中,得到对应的控制量,进而对比实际值与控制值之间的误差。
四、实现
% 网络迭代优化
for k=1:1:200 %% 系统输出 -- 实际值y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%% 系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%% 输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%% 隐含层 x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%% 比例神经元kp计算kp=[x1i(1),x2i(1),x3i(1)];kp(find(kp>kpmax)) = kpmax;kp(find(kp<kpmin)) = kpmin;qp=kp;%将kp系数作为输入神经元h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);%% 积分神经元ki计算ki=[x1i(2),x2i(2),x3i(2)];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+ki; %将ki系数作为输入神经元qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%% 微分神经元kd计算kd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];kd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=kd-kd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%% 输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %% 计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)]; error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%% 隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo'; w21=w21+rate2*dw21+rate3*(w21_1-w21_2);%调整w22Sig2=sign(ypc./(uh(2)+0.00001));dw22=sum(error.*Sig2)*qo';w22=w22+rate2*dw22+rate3*(w22_1-w21_2);%调整w23Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23+rate3*(w23_1-w23_2);%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001));endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));ends1=sgn'*[r1(k),y1(k)];wshi2_1=wshi(1:3,1:3);alter=zeros(3,1);dws1=zeros(3,2);for j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1+rate3*(w11_1-w11_2);%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001));ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2+rate3*(w12_1-w12_2);%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001));ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);endw13=w13+rate1*dws3+rate3*(w13_1-w13_2);%% 参数更新u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;w11_1=w11;w11_2=w11_1;w12_1=w12;w12_2=w12_1;w13_1=w13;w13_2=w13_1;%第二层权值w21_1=w21;w21_2=w21_1;w22_1=w22;w22_2=w22_1;w23_1=w23;w23_2=w23_1;
end上述是整个迭代过程,下面看看具体的输出结果:
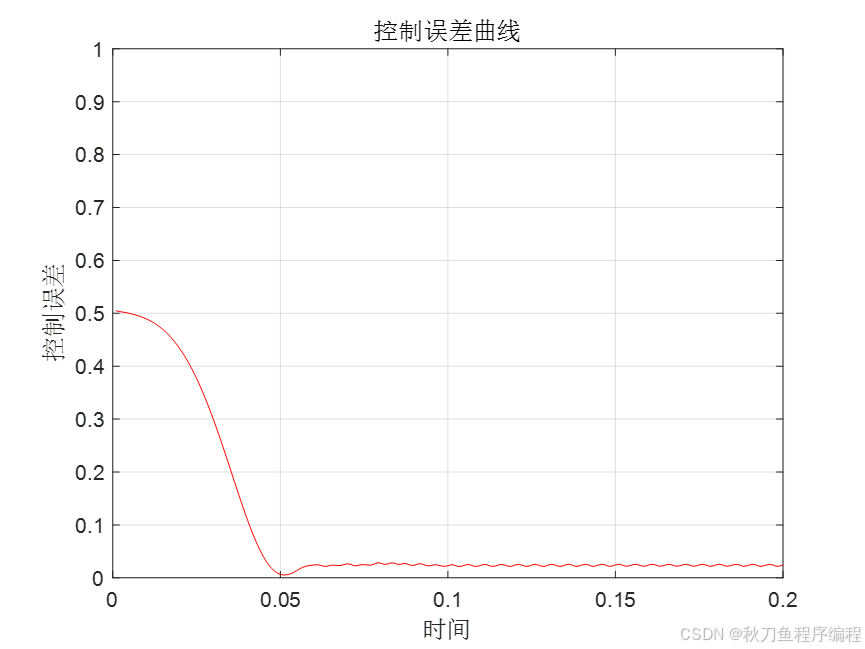
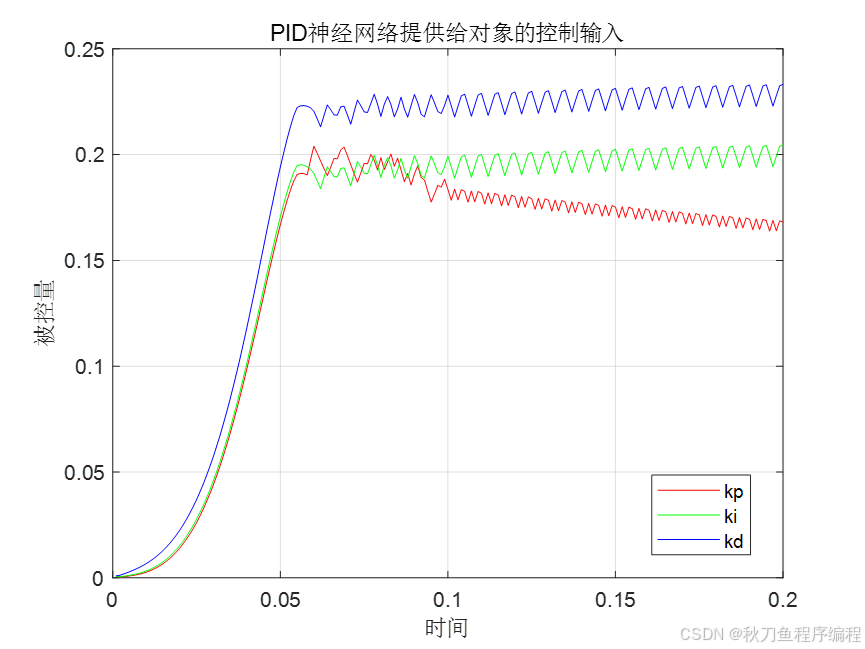
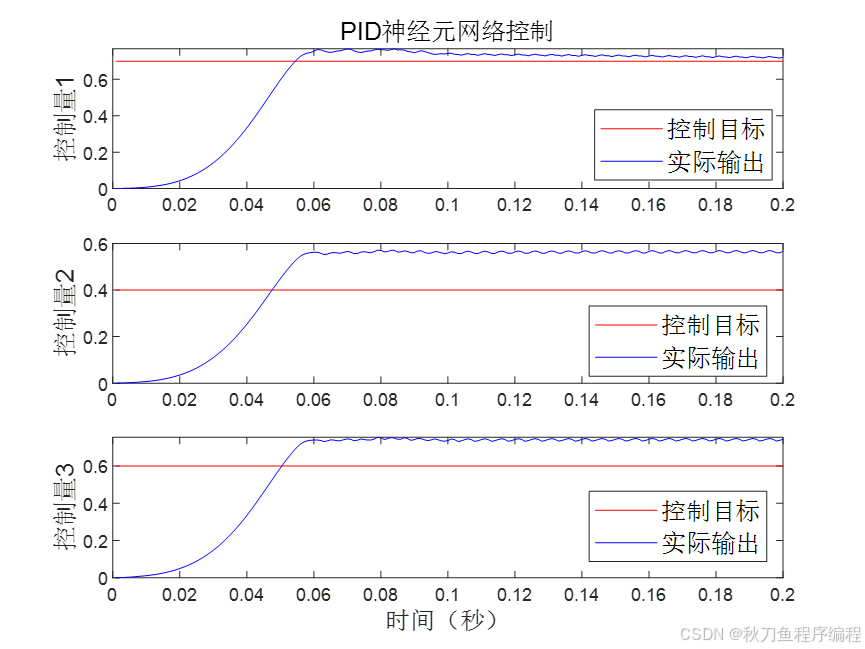
神经网络做PID控制,需要大量的样本进行训练,以此得到比较好的PID系数!
