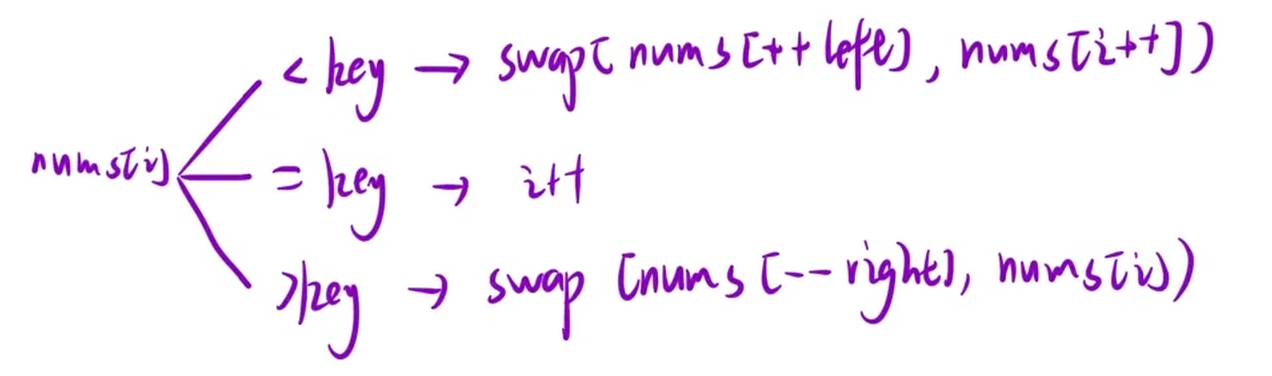【算法】——分治思想与快速排序的实践应用
前言:
本篇文章会先介绍一下快速排序算法,然后重点是快速排序在一些算法题中的应用,在使用当中感受快速排序的魅力。(本篇文章主要使用C++语言)
一、什么是快速排序?
1. 简单介绍
首先它是一种优化的排序算法。常规的排序通常是O(n^2)的时间复杂度,而快速排序的时间复杂度是O(n*lgn),这样一来在数据量大的情况下就可以节省大量时间。
2. 如何实现
分治思想是快速排序算法的核心思想。分治即分而治之,将一个很难完成的大任务拆分成一个个很好完成的小任务,然后完成每一个小任务进而间接完成大任务。
快速排序的实现过程可以概括为三个步骤:
1. 选取基准值(从数组中随机选取一个数据作为基准值)
2. 分区(将比基准值小的放到基准前面,比基准值大的放到基准后面)
3. 递归(再对分好区的两边重复1,2,3步,直至不可分为止)
可以借助这张图理解:
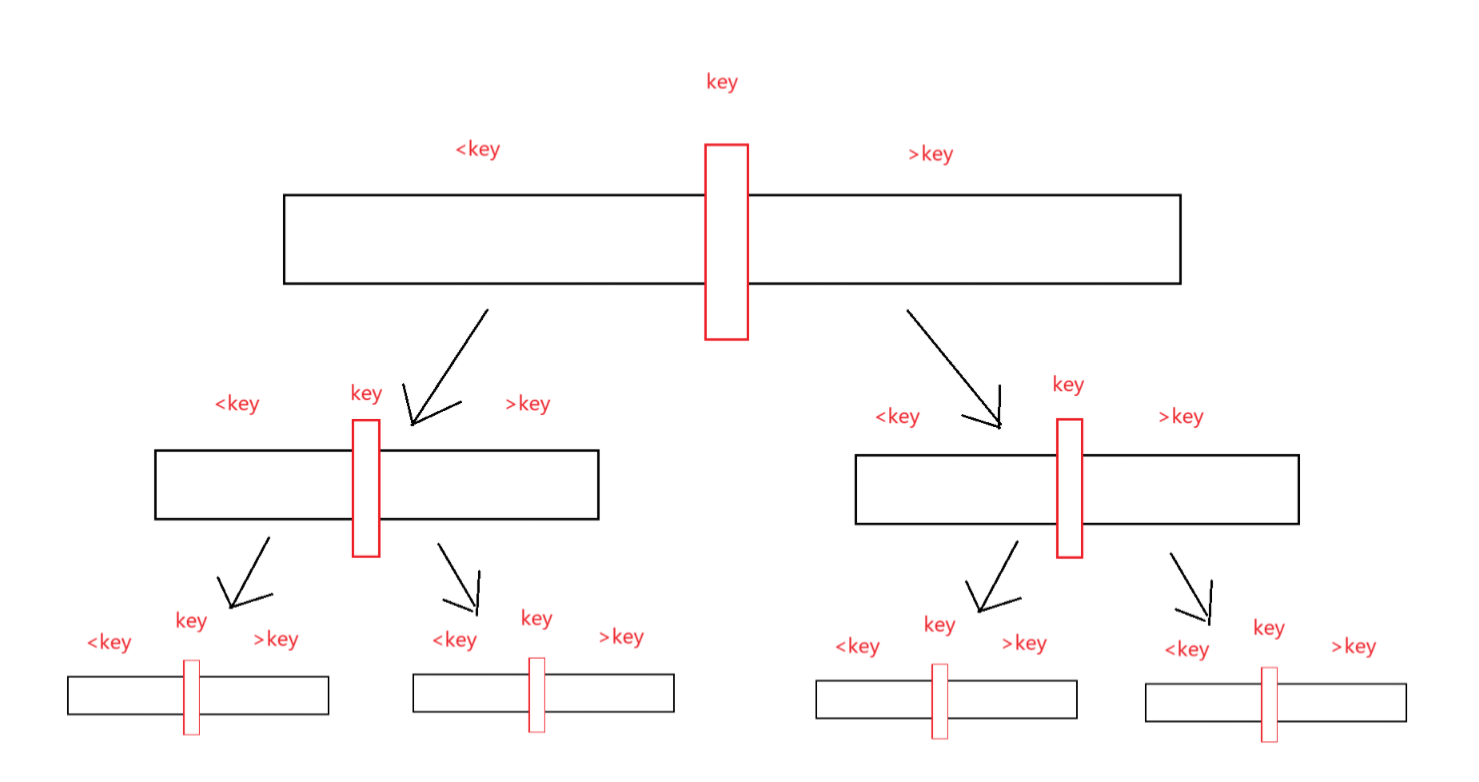
先介绍一个分为两个区间,使用hoare方法的实现方式:
1. 这里为了简化,基准值取第一个元素
2. right从右往左走,找比基准值小的数据,left从左往右走,找比基准值大的数据
3. 找到之后交换left和right的数值,再left++, right--,重复第二步
4. 最后再将基准值换到中间
示例代码:
//hoare方法
int _quicksort(int* arr, int left, int right) {//基准值取第一个元素int keyi = left;//先将left+1,使其移到基准值的后一个位置left++;//right从右往左走,找比基准值小的数据,left从左往右走,找比基准值大的数据while (left <= right) {if (arr[right] >= arr[keyi]) {right--;}else if(arr[left] <= arr[keyi]) {left++;}else {Swap(&arr[left], &arr[right]);left++;right--;}}//交换数组第一个数据和 左数组的最后一个数据,实现基准值归位到中间Swap(&arr[keyi], &arr[left - 1]);keyi = left - 1;return keyi;
}void QuickSort(int* arr, int left, int right) {//快速排序借鉴了二叉树的思想,在数组中找一个基准值,然后将小的数据放在基准值左边,大的数据在右边, 然后在对左右数组循环此操作if (left >= right) {return;}int keyi = _quicksort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}接下来介绍分为三个区间的实现方法:
1. 用随机数求一个key
2. 定义left, right, i
3. [0, left]最终表示<key的数据区域, 而[right, n-1]表示最终>key的数据区域
4. i从0开始遍历到n-1,小于key的就和++left交换,大于key的就和--right交换(由于[0, left]是闭区间,所以交换前left需要先+1再交换,来接纳一个新的<key的数,right同理)
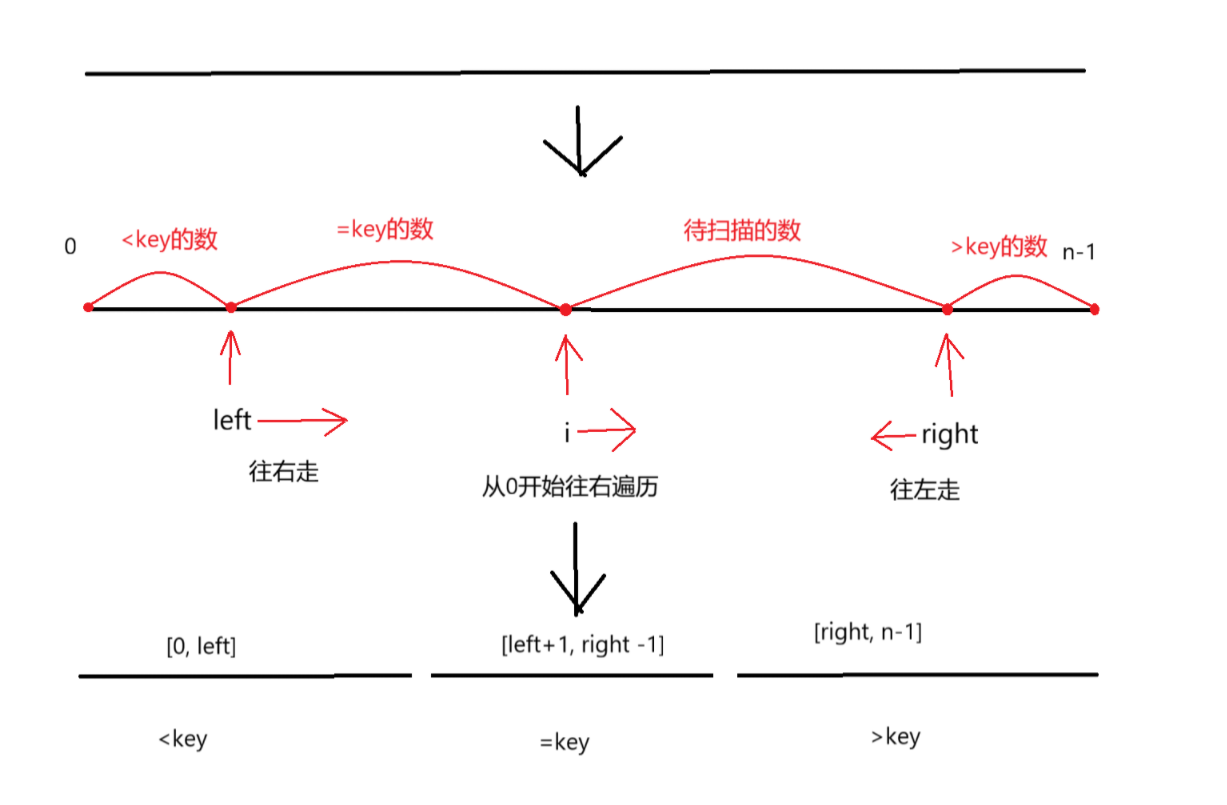
由于没有情景看代码比较抽象,所以我们接下来直接配合题目来看代码
二、快速排序使用实例
1. 颜色分类

这道题要求把数组分为红白蓝三色,实际就是将数组按0,1,2的顺序排序。那我们用快速排序就能快速解决,key也不用随机了,直接key = 1
void sortColors(vector<int>& nums) {// 快速排序int left = -1;// 排序后[0, left]的数据都是0int right = nums.size();// 排序后[right, nums.size()-1]的数据都是2int i = 0;// 排序后[left+1, right-1]的数据都是1while(i < right){if(nums[i] < 1){swap(nums[++left], nums[i++]);}else if(nums[i] == 1){++i;}else{// 因为初始右边数据是无序的,所以与right交换时i不++,而是需要再判断一次swap(nums[--right], nums[i]);}}
}1. left初始化为-1, right初始化为size(), 表明初始情况下左右区间都是空,全是待扫描数据
2. 然后i从0开始遍历,进行以下操作:
2. 排序数组

主程序调用qsor排序即可,不过要注意要加上srand(time(NULL))设置随机数种子
vector<int> sortArray(vector<int>& nums) {srand(time(NULL));qsort(nums, 0, nums.size()-1);return nums;
}随机数生成key的函数:
int getRandom(vector<int>& nums, int left, int right){int r = rand();r = r%(right - left + 1) + left;return nums[r];
}重点来看qsort的实现:
1. l和r是数组是左右边界,当l >= r时结束递归
2. 定义left和right,用于分区,i从l开始遍历
3. 将nums [i] 和key比较,并进行相应的交换操作
4. 对左右两块区域进行递归调用qsort,区间分别是[l, left]和[right, r]
void qsort(vector<int>& nums, int l, int r){if(l >= r){return;}int left = l-1;int right = r+1;int i = l;int key = getRandom(nums, l, r);while(i < right){if(nums[i] < key){swap(nums[i++], nums[++left]);}else if(nums[i] == key){i++;}else{swap(nums[i], nums[--right]);}}qsort(nums, l, left);qsort(nums, right, r);}3. 快速选择排序解决topk问题

快速排序可以分区,那么当遇到topk问题时,每次分完区后topk会落在某一段区间内,那么剩下的区间我们就可以舍弃,这样就可以大大提高寻找效率。
随机生成k部分还是一样
int getRandom(vector<int>& nums, int left, int right){int r = rand();r = r%(right - left + 1) + left;return nums[r];}主函数也差不多
int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort(nums, 0, nums.size()-1, k);}重点看qsort部分:
1. 递归结束条件改为了l == r,结束后直接返回nums[l],这就是我们要求的第k大的数据、
2. 分类讨论时定义c为>key区域的数据个数, b为=key区域的数据个数
3. 情况一:如果c >= k,说明目标数据在第三个区域,那直接舍弃前两个再递归
4. 情况二:如果b + c >= k,说明目标数据在第二个区域,直接返回key
5. 情况三:目标在第一个区域,舍弃后两个区域再递归
int qsort(vector<int>& nums, int l, int r, int k){if(l == r){return nums[l];}int left = l-1;int right = r+1;int i = l;int key = getRandom(nums, l, r);while(i < right){if(nums[i] < key){swap(nums[i++], nums[++left]);}else if(nums[i] == key){i++;}else{swap(nums[i], nums[--right]);}}// 分类讨论int c = r - right + 1, b = right - left -1;if(c >= k){return qsort(nums, right, r, k);}else if(b + c >= k){return key;}else{return qsort(nums, l, left, k - b - c);}}总结:
本篇文章介绍了分治与快速排序算法,并用了三道例题来讲解,如果觉得右帮助的话可以点赞收藏加关注支持一下!