LabVIEW 模拟单摆运动（DAE 法）

​LabVIEW利用 DAE Radau 5th Order VI，通过微分代数方程（DAE）对单摆运动进行模拟，可改变初始位置观察单摆摆动情况，理解 DAE 在动力学模拟的应用。

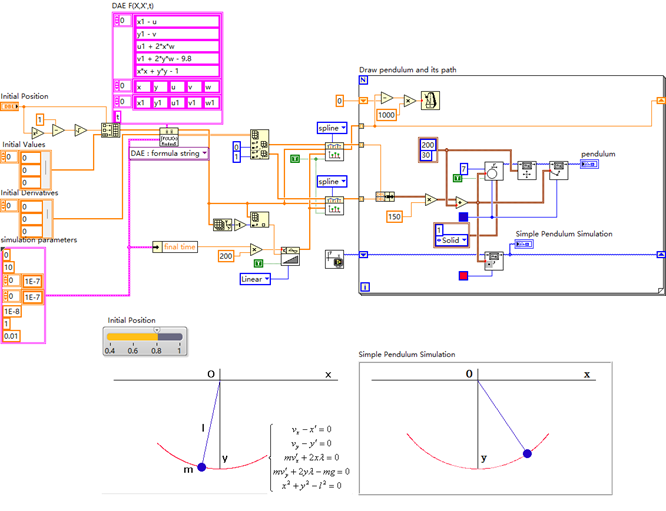
微分代数方程（DAE）是同时包含微分方程和代数方程的方程组，在动力学、控制等领域，用于描述含约束的系统，单摆因摆长约束，其运动可用 DAE 建模。

VI 说明

• DAE Radau 5th Order VI

• • 功能：采用 5 阶 Radau 方法求解微分代数方程，用于模拟含约束的动态系统，如单摆运动。

  • 使用场合：适用于需高精度求解 DAE 的场景，像复杂多体动力学、化工过程等含约束的动态过程模拟。

  • 特点：5 阶精度，对刚性 DAE 有良好适应性，能稳定求解含约束系统。

  • 使用注意事项：需合理设置模拟参数（如最终时间、容差等），初始条件要与系统物理意义一致；因引入拉格朗日乘数处理约束，要注意乘数精度相关的容差设置。

  • 类似功能对比：与 “ODE Solver VI”（常微分方程求解）相比，DAE Radau 5th Order VI 可直接处理含代数约束的 DAE，而 ODE Solver VI 仅适用于纯微分方程系统，在含约束系统模拟上，DAE VI 更具针对性。

• Wait Until Next ms Multiple VI

• • 功能：使循环迭代时间与前面板显示一致，保证界面显示的时序稳定性。

  • 使用场合：在需要同步循环执行与界面显示更新的场景，如实时模拟、数据可视化等。

  • 特点：简单易用，能有效控制循环时序，提升界面显示的流畅性与一致性。

  • 使用注意事项：需根据显示需求合理设置毫秒倍数，避免因设置不当导致显示延迟或卡顿。

  • 类似功能对比：与 “Wait (ms) VI”（固定毫秒等待）相比，“Wait Until Next ms Multiple VI” 能更好地与系统时钟同步，使循环周期更稳定，适合对显示时序要求高的场景，“Wait (ms) VI” 则更适合简单的固定延迟需求。

背景补充

单摆是经典动力学系统，其摆长固定的约束使其运动方程为 DAE。LabVIEW 的 DAE 求解 VI 为工程师提供了便捷工具，无需深入复杂数值算法，即可实现含约束动态系统的模拟，在教学、工程仿真等领域应用广泛。