深度学习笔记(一)——线性回归、Softmax回归、多层感知机、环境和分布偏移

写在前面：

写本系列(自用)的目的是回顾已经学过的知识、记录新学习的知识或是记录心得理解，方便自己以后快速复习，减少遗忘。深度学习主要看的是李沐老师的视频，书是李沐老师的动手学深度学习。笔记也基本来于此。

part1 线性神经网络

一、线性回归

在机器学习领域中的大多数任务通常都与预测有关。 当我们想预测一个数值时，就会涉及到回归问题。 常见的例子包括：预测价格（房屋、股票等）、预测住院时间（针对住院病人等）、 预测需求（零售销量等）。

1、线性回归的基本元素

假设我们希望根据房屋的面积和房龄估算房屋价格。 为了开发一个能预测房价的模型，我们需要收集一个真实的数据集。 这个数据集包括了房屋的销售价格、面积和房龄。 该数据集称为训练集。 每行数据称为样本。试图预测的目标称为标签或目标。 预测所依据的自变量称为特征。

(1)线性模型

可以对目标进行线性假设：

其中的w称为权重，权重决定了每个特征对我们预测值的影响。b称为偏置值，指当所有特征都取值为0时，预测值应该为多少。没有偏置项，模型的表达能力将受到限制。将模型拓展到高维：

其中，x为n×d维向量，其中行表示样本数，列表示特征数。w为d维向量，b为n为向量。

(2)损失函数

损失函数能够量化目标的实际值与预测值之间的差距。通常会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。回归问题最常用的损失函数为平方损失函数：

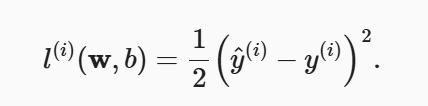
其中y_hat为预测值，y为真实值。在训练模型时，我们使用的是所有样本的损失均值：

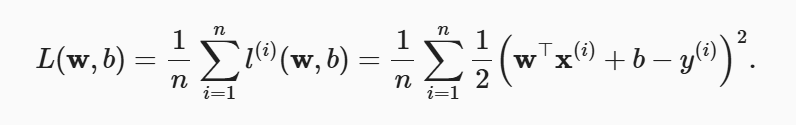
为了使模型效果更好，我们需要找到一组参数w和b使得损失值最小，这就是w和b的求解方向：

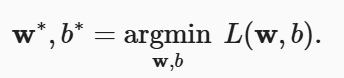
(3)随机梯度下降

线性回归有解析解，但不是所有问题都有解析解，因此这里还是当作没有解析解进行求解。

梯度下降方法几乎可以优化所有深度学习模型。 它通过不断地在损失函数递减的方向上更新参数来降低误差。假设损失函数为J，对w和b分别求导，得：

 

那么更新法则为：

 

 

这个公式在以前的博客里有写过：https://blog.csdn.net/qq_65078669/article/details/149288569?fromshare=blogdetail&sharetype=blogdetail&sharerId=149288569&sharerefer=PC&sharesource=qq_65078669&sharefrom=from_link

可以看出在每一次更新参数之前，必须遍历整个数据集，这会很慢。 因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本， 这种变体叫做小批量随机梯度下降。

在每次迭代中，首先随机抽样一个小批量β， 它是由固定数量的训练样本组成的。 然后，我们计算该小批量的平均损失关于模型参数的导数。 最后，我们将梯度乘以学习率，并从当前参数的值中减掉。(就是把以前除以样本数改成了除以β的长度)

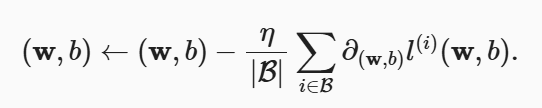
批量大小β和学习率η的值通常是手动预先指定，而不是通过模型训练得到的。 这些可以调整但不在训练过程中更新的参数称为超参数。 调参是选择超参数的过程。 

(4)预测

在训练完模型后就可以进行预测了。

2、从线性回归到深度网络

我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。

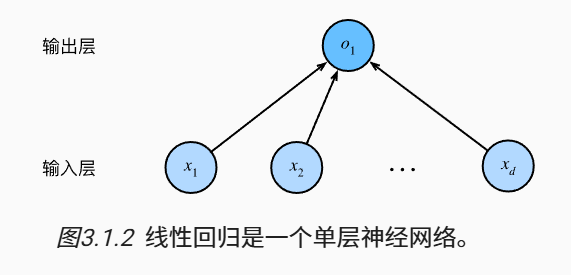
对于线性回归，每个输入都与每个输出相连， 我们将这种变换称为全连接层或称为稠密层。

3、部分练习题

1、什么时候使用平方误差的线性回归解析解可能比使用随机梯度下降更好？这种方法何时会失效？

答：当数据量不大时，解析解方法通常比随机梯度下降更好。因为解析解可以直接通过矩阵运算一次性得到最优的参数w，不需要进行迭代优化，能够快速、精确地得到结果，不存在收敛速度慢或者需要调整学习率等问题。

失效：当数据量非常大时，计算矩阵XTX的逆（或求解相关矩阵方程）会占用大量的内存和计算资源，甚至可能超出计算机的处理能力，导致计算无法进行。

当矩阵XTX是奇异矩阵（即行列式为0，不可逆）时，解析解方法无法直接使用。这种情况可能出现在特征之间存在线性相关（多重共线性）等场景下。

2、如果我们将权重初始化为零，会发生什么。算法仍然有效吗？

线性模型：权重初始化为零可行，但不推荐（通常用随机初始化加速收敛）。

神经网络：权重初始化为零不可行，会导致对称权重问题，模型无法学习。

二、Softmax回归

softmax适用于分类问题，是一种单层神经网络。

softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。

1、网络架构

为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。例如，对于4个特征，3个输出，在神经网络中有如下神经网络图：

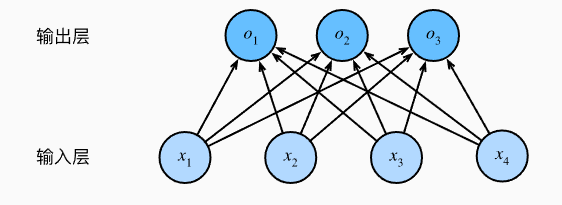
公式可以表示为：

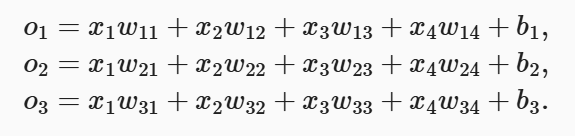
其中，12个w为权重，3个b为偏置。可以利用线性代数知识简单地将其表示为：，这样就将12个权重放入了一个3×4的矩阵中。

2、全连接层

全连接层是“完全连接”的，对于上文提到的那个单层神经网络，就是一个全连接层。对于任何具有个输入和个输出的全连接层， 参数开销为O(dq)。也可以将其成本减少到，其中n可以由我们指定。

3、Softmax运算

在分类问题的预测中，假如得到的预测值y1、y2、y3分别是0.1，0.8，0.1，那么我们预测的类别就取最大预测值，即预测的类别是y2。但是为规范化的预测o不能直接视作我们感兴趣的输出。因为，一方面，我们没有限制这些输出数字的总和为1。 另一方面，根据输入的不同，它们可以为负值。

Softmax函数可以解决这个问题，它能将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质，公式为：

并且在规范化后，仍然使用下式来选择最有可能的类别：

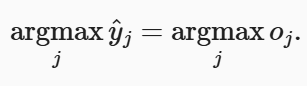
4、小批量样本的矢量化

为了提高计算效率并且充分利用GPU，通常会对小批量样本的数据执行矢量计算。假设读取了一个批量的样本X， 其中特征维度（输入数量）为d，批量大小为n。 假设输出中有q个类别。 那么小批量样本的特征为， 权重为， 偏置为。 softmax回归的矢量计算表达式为：

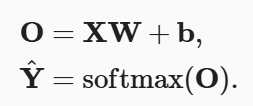
5、损失函数

(1)交叉熵损失函数

分类与回归任务不同，只需要正确的预测值比其他几个预测值大就可以，不管其他两个预测值为多少，类别预测均正确。而平方损失过于严格，更加适合衡量两个概率分布差异的测量函数是交叉熵损失函数：

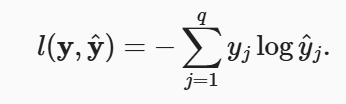
(2)导数

交叉熵损失的导数为：

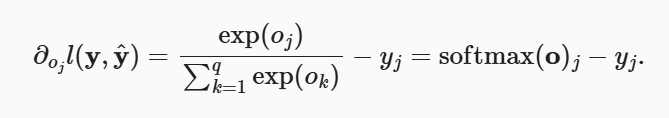
part2 多层感知机

一、多层感知机

1、隐藏层

线性模型有很多局限性，很多东西不能用线性模型来简单描述。在网络中加入一个或多个隐藏层可以克服线性模型的限制，使其能处理更普遍的函数关系类型。

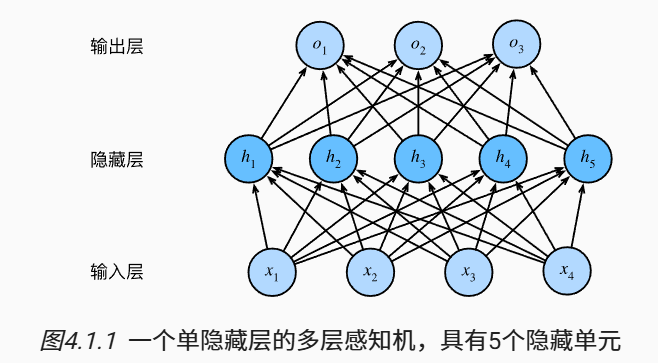
这种架构通常称为多层感知机，通常缩写为MLP。这两个层都是全连接的。

(1)从线性到非线性

在引入隐藏层后，计算输出的方式变为：

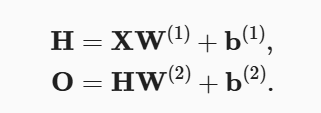
其中，X为n×d维向量，W1为d×h维向量，H为n×h维向量，b1为1×h维向量，W2为h×q维向量，b2为1×q维向量，O为n×q维向量。

仅这样添加隐藏层，依然是线性模型：

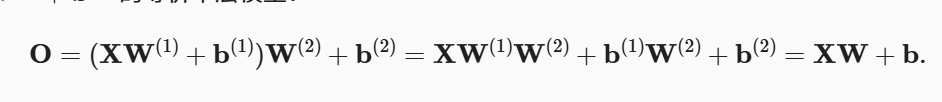
为了多层感知机不退化为线性模型，还需要使用非线性的激活函数：

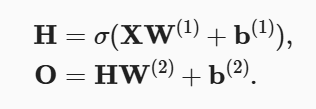
2、激活函数

激活函数的核心作用是为神经网络引入非线性，使模型能够拟合复杂的非线性关系。其运算过程确实涉及对 “加权和 + 偏置” 的转换，但本质是通过非线性变换让神经网络突破线性模型的局限。大多数激活函数都是非线性的。

(1)ReLU

ReLu最受欢迎的激活函数。

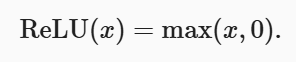
ReLU图像：

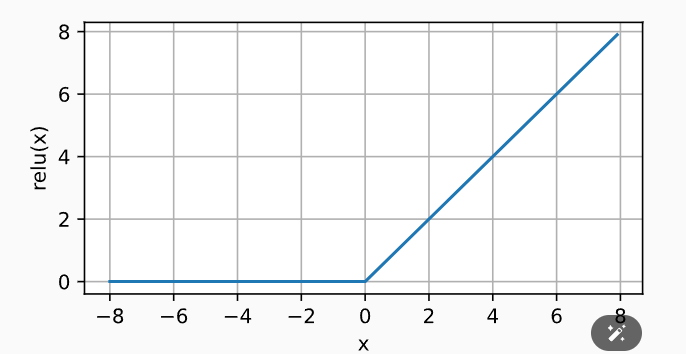
ReLU导数图像：

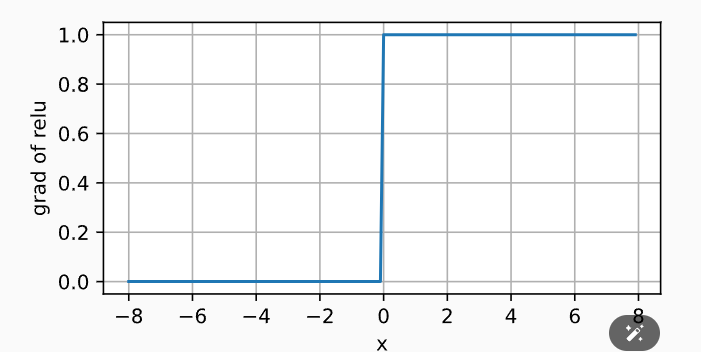
使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。ReLU减轻了困扰以往神经网络的梯度消失问题。

(2)Sigmoid

 sigmoid函数将输入变换为区间(0, 1)上的输出。 它将范围（-inf, inf）中的任意输入压缩到区间（0, 1）中的某个值。

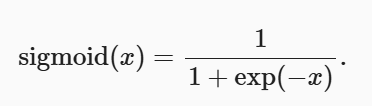
Sigmoid图像：

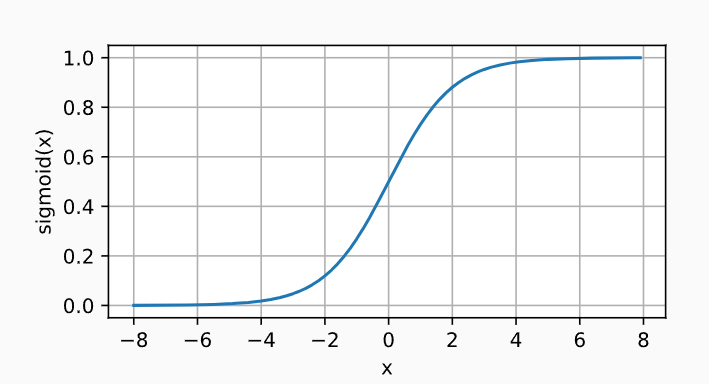
Sigmoid导数：

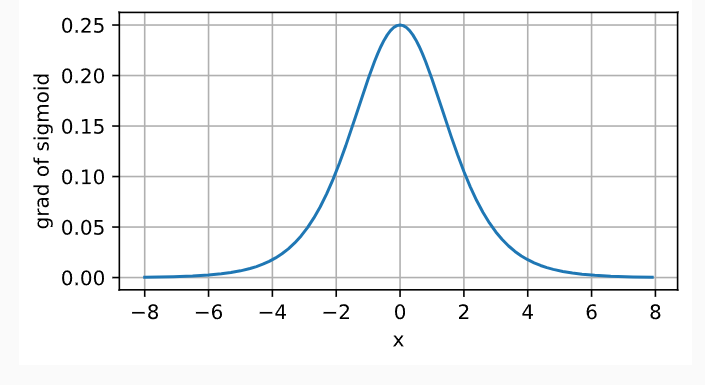
(3)tanh

与sigmoid函数类似， tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下：

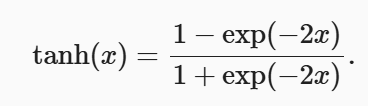
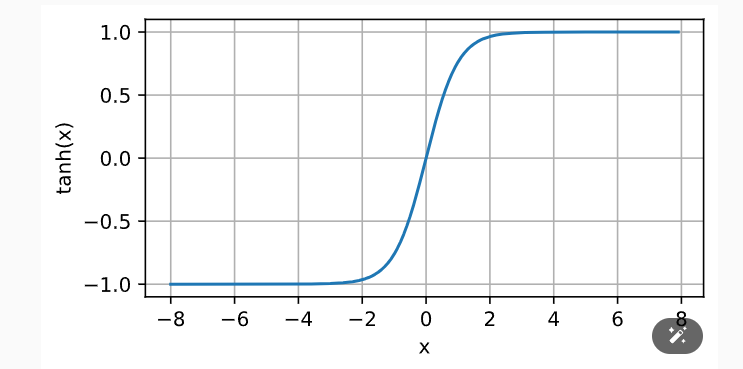
tanh的图像是：

tanh的导数是：

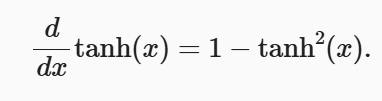
tanh的导数图像是：

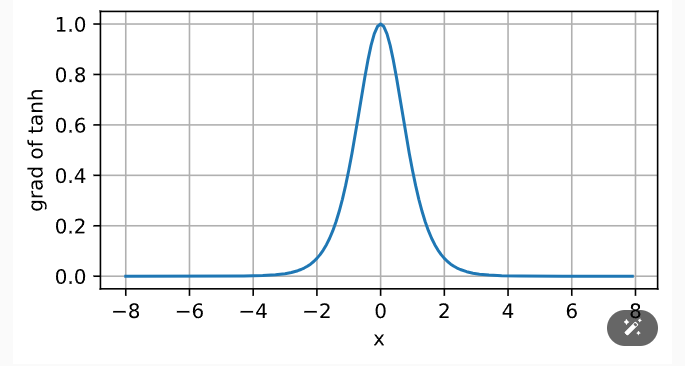
二、正则化方法

1、权重衰减

为了解决过拟合问题，需要引入正则化技术。权重衰减是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化。

对于一个模型而言，权重小的模型会更加简单。直观理解就是：

当权重 w 的模很小时：输入 x 的微小变化（比如特征中有噪声、或测试数据与训练数据有差异），对输出 f(x) 的影响也会很小。这意味着模型的输出更 “平缓”，不会因输入的小波动而剧烈变化，更能捕捉稳定的、不依赖个别样本的规律。

当权重 w 的模很大时：输入的微小变化可能导致输出剧变，模型会对输入中偶然的、噪声性的细节过度敏感，从而把这些细节错误地当作 “规律” 学习，导致过拟合。

权重衰减就是要保证权重不会过大。之前提到的损失函数是：

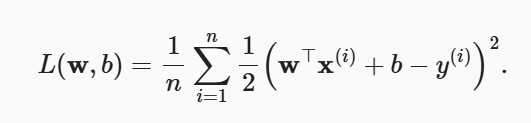
可以在损失函数中引入权重w：

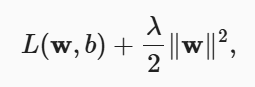
我们需要对损失函数取最小值，当权重的增大带来的损失函数减小不多时，权重就不会再继续增大了，这对权重起到了限制作用。λ为正则化常数。那么，此时的小批量随机梯度下降更新公式为：

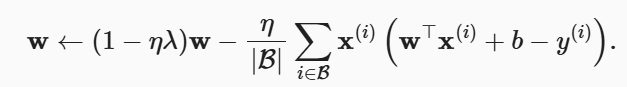
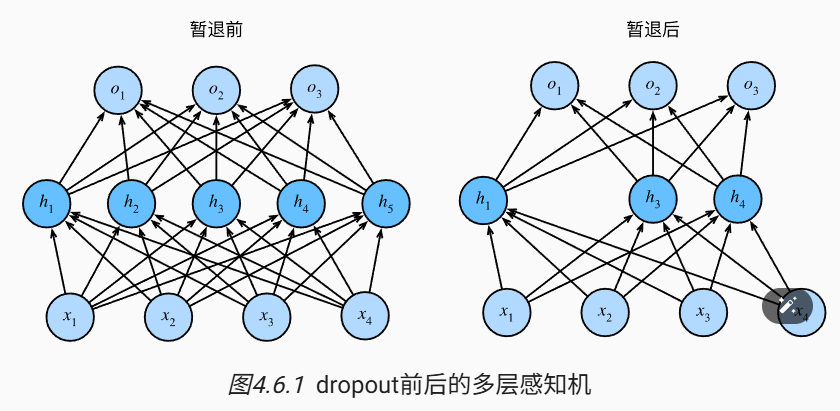
2、暂退法(Dropout)

简单理解dropout就是在训练过程中丢弃一些神经元。例如，在以下神经网络的训练中，以p的概率将隐藏单元置为0。比如图下，删除了h2和h5，输出的计算不再依赖于h2和h5，各自的梯度在反向传播时也会消失。

三、前向传播、反向传播

前向传播指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

反向传播指的是计算神经网络参数梯度的方法。该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。 该算法存储了计算某些参数梯度时所需的任何中间变量（偏导数）。 

四、数值稳定性和模型初始化

初始化方案的选择在神经网络学习中起着举足轻重的作用， 它对保持数值稳定性至关重要。糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。

1、梯度消失和梯度爆炸

假设有一个L层，输入为x输出为o的深层神经网络，每一层由变换fl定义，第l层的权重为W(l)，网络可以表示为：

在反向传播求梯度时，公式为：

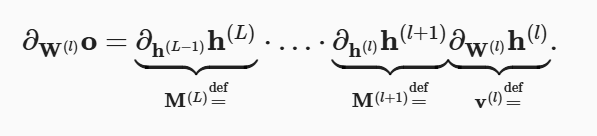
梯度是乘积的形式，因此，我们容易受到数值下溢问题的影响. 当将太多的概率乘在一起时，这些问题经常会出现。而在处理概率时，若切换到对数空间，可能会数值上溢。

梯度消失指的是：参数更新过小，在每次更新时几乎不会移动，导致模型无法学习。

梯度爆炸指的是：参数更新过大，破坏了模型的稳定收敛。

2、对称性

神经网络的对称性指的是： 如果将隐藏层的所有参数初始化为常量C。

在前向传播期间，两个隐藏单元采用相同的输入和参数， 产生相同的激活，该激活被送到输出单元。 在反向传播期间，根据参数对输出单元进行微分， 得到一个梯度，其元素都取相同的值。 因此，在基于梯度的迭代（例如，小批量随机梯度下降）之后， 的所有元素仍然采用相同的值。 这样的迭代永远不会打破对称性，我们可能永远也无法实现网络的表达能力。 隐藏层的行为就好像只有一个单元。

虽然小批量随机梯度下降不会打破这种对称性，但暂退法正则化可以。

3、初始化

解决上述问题的方法就是正确地初始化。

(1)默认初始化

使用正态分布来初始化权重值。

(2)Xavier初始化

通常，Xavier初始化从均值为零，方差为的高斯分布中采样。这是为了保证初始化输入x得到的输出o的均值和方差的不变性。

也可以从均匀分布中抽取权重时的。此时初始化值域为：

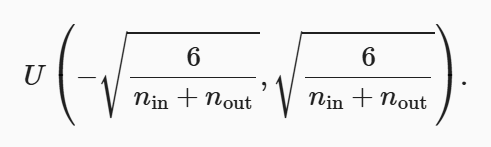
五、环境和分布偏移

1、分布偏移

分布偏移​​ 指的是模型在​​训练时​​看到的数据（训练集）和它在​​实际应用时​​会遇到的数据（测试集或真实世界的数据）在​​统计特性上发生了变化​​。

例如，教学生时用的全是哈士奇和布偶猫的图片（训练分布），但考试时却让他去分辨所有的狗和猫（测试分布），他很可能因为没见过吉娃娃或无毛猫而认错。

有一种最极端的分布偏移情况。训练和测试时，正常情况下猫狗图片的风格、品种都差不多，规则是猫就是猫，狗就是狗。

但极端的情况是，测试时，猫狗图片的风格、品种都差不多，但答案相反了，此时规则是猫是狗，狗是猫。就会导致输入的图片看起来完全没有变化，但模型完全不能察觉到规则已经变了，就会一直出错，却不知道原因。

以上例子说明：如果没有任何关于pS(训练分布)和pT(测试分布)之间相互关系的假设，学习到一个分类器是不可能的。

我们可以通过检测偏移并进行动态调整来解决这个问题。

2、真实风险和经验风险

打个比方：假如你要参加高考，

真实风险就是你的​​最终高考成绩​​。它反映了你真正的、全面的知识水平，代表了你面对任何未知考题的能力。这就是我们学习的终极目标。

经验风险就是你做的​​历年高考真题模拟卷的得分​​。这些卷子（训练数据是有限的，但它是我们用来评估和提升自己水平的最主要工具。

3、协变量偏移修正

打个比方，当你的训练数据(刷的题)和真实数据(高考)的出题风格不一样时，需要给那些更像高考题的训练题更高的权重，让模型更重视它们。

(1)协变量偏移

你是一名A省的考生

训练数据分布q(x)：你手头只有​​B省的模拟考试题（B省以难、怪著称，出题风格和A省不一样）。

真实数据分布p(x)：A省高考

这就产生了协变量偏移：输入特征 x（考题）的分布发生了变化，但背后要考察的知识点 P(y|x)（比如函数、几何）是一样的。如果你拼命刷B省的怪题、难题，虽然把这些题都做对了（经验风险最小化），但可能对备战B省高考帮助不大，甚至有害。

(2)偏移修正

解决方案是：重要性权重β。

假如此时有个老师告诉你：我这里有​​A省高考历年真题​​（来自分布 p(x)）。虽然不多，但我们可以用它来找出你的B省模拟题中，​​哪些题最像A省高考题​​。对于这些题，就多花时间研究；对于那些怪题，就少花点时间。

这个像不像的程度，就是权重β_i = p(x_i) / q(x_i)。

如果一道B省题 x_i的风格非常像A省高考题（即 p(x_i)大，q(x_i)小），那么它的权重 β_i就会很大，模型在训练时会更关注这个样本。反之减少对其的关注。

(3)权重计算方式

可以利用对数几率回归法来估计权重β。

​1、首先把少量的A省高考真题(p(x))和B省模拟题(q(x))混在一起

2、给所有的A省题打标签z=1，B省题打标签z=-1。

3、训练分类器，这个分类器的任务是判断一道题来自A省还是B省。

如果分类器很容易就能判断一道题是B省的，说明这道题补兑，权重β应该小

如果分类器很难分辨一道题是A还是B的，就说明这道题风格很像，权重应该大

4、通过分类器预测的概率，可以直接计算出每个样本的权重​ β_i = exp(h(x_i))

4、标签偏移修正

当你的训练数据（刷的题）和真实考试（高考）的题目比例不一样时，你需要调整模型对不同类型题目的重视程度，让模型更适应真实考试的题目分布。​

(1)标签偏移

训练数据分布 q(y)​​：你手头的​​模拟考试卷​​中，​​数学题占60%​​，语文题占30%，英语题占10%。

真实数据分布 p(y)​​：但实际的​​高考真题​​中，​​数学题只占30%​​，语文题占40%，英语题占30%。

​这就产生了“标签偏移”​​：标签 y（题目类型）的分布发生了变化，但每类题目的​​出题风格和难度​​ p(x|y)是一样的。

(2)偏移修正

根据​​真实高考的题目比例​​来调整复习时间。对于高考中比例增加的科目，应该分配更多时间；对于比例减少的科目，可以适当减少时间。

这个调整复习事件的系数，就是权重β_i = p(y_i) / q(y_i)​​。例如：

对于语文题：β_语文 = 0.4 / 0.3 ≈ 1.33> 1，权重增加

(3)计算权重

q(y)是训练集的标签分布，我们是知道的。但 p(y)是测试集的​​真实​​标签分布，我们不可能知道测试数据的真实标签，否则就不需要预测了。为了计算出p(y)，使用混淆矩阵方法。

1、训练一个分类器。这里用的是训练数据，假如训练一个三分类任务（猫，狗，鸟）

2、计算混淆矩阵C。准备一个验证集（同样来自于训练分布）。用训练模型与预测这个验证集。可以得到一个混淆矩阵C：

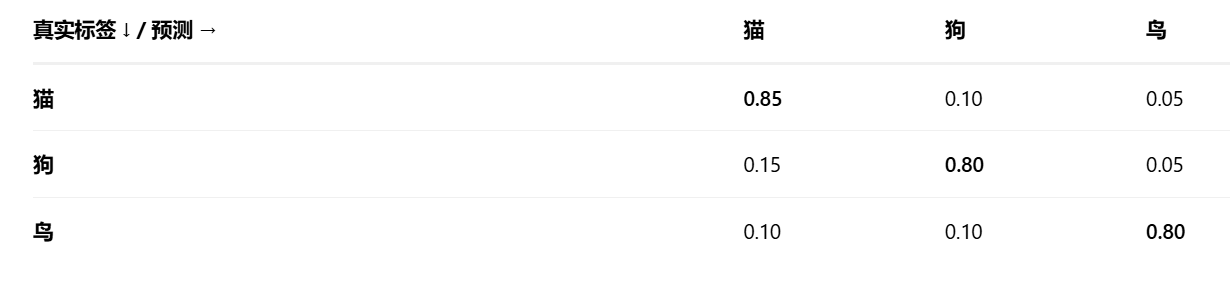
混淆矩阵表达的是，模型有85%的概率将猫预测正确，10%概率误判为狗，5%概率误判为鸟。

3、估计测试集的标签分布p(y)。直接用训练好的模型去预测整个测试集，统计模型在测试集上的预测输出μ(y)，例如μ(y)=[0.4, 0.4, 0.2]。这意味着，模型预测的结果中，有40%的样本被判断为“猫”，40%被判断为“狗”，20%被判断为“鸟”。

也就是说C*p(y) = μ(y)。将知道的数字代进去：

可以求解出p(y)。p(y) = [0.35, 0.45, 0.2]。这样，就可以得到β了。