当前位置：首页 > news >正文

【读论文】AI笔记（一）9月26日组会前

news 2025/9/28 5:22:27

令人呼吸一滞的目录——

都是压缩，有何不同？

1. 物理本质：量子调控 vs 信号处理

2. 技术实现：量子光学 vs 电子 / 算法

3. 应用目标：突破极限 vs 优化听感

4. 数学模型：量子算符 vs 动态函数

5. 术语起源：量子物理 vs 工程实践

总结：本质差异的直观对比

为什么低不确定度和高精度要分开说？

关于相干态所决定的量子散粒噪声极限

第一步：先明确核心概念 —— 什么是 “相干态的量子散粒噪声极限（SNL）”

第二步：拆解方案 A 和 B—— 为何它们都逃不出 SNL 的束缚？

1. 方案 A（直接光学吸收探测）：相干态的 “线性衰减” 不改变量子噪声特性

2. 方案 B（拍频探测）：“频率转换” 不改变噪声的量子本质

第三步：关键总结 ——“达到极限” 的本质原因

延伸：如何突破 SNL？

极化和非线性

一、先明确基础：什么是 “极化率 χ⁽ⁿ⁾”？

二、χ⁽²⁾（二阶）非线性：依赖 “非中心对称介质” 的效应

1. 核心特点：介质必须 “非中心对称”

2. 典型物理过程（与压缩光相关）

3. 优势与局限

三、χ⁽³⁾（三阶）非线性：“中心对称 / 非对称介质均可产生” 的效应

1. 核心特点：无介质对称性限制

2. 典型物理过程（与压缩光相关）

3. 优势与局限

四、核心对比：χ⁽²⁾ vs χ⁽³⁾非线性（表格总结）

五、结合原文语境：为什么选择 χ⁽³⁾非线性？

【都是压缩，有何不同？】

在压缩双光梳光谱（Squeezed Dual-Comb Spectroscopy）中的 squeeze（压缩）与混音中的 compressor（压缩器）虽然中文均译为 “压缩”，但二者的物理本质、技术实现和应用目标存在根本差异，具体可从以下五个维度对比分析：

1. 物理本质：量子调控 vs 信号处理

光学中的 Squeeze是量子态的操控，通过非线性光学过程（如克尔效应）改变光场的量子涨落分布。例如，压缩态光场的某一正交分量（如幅度或相位）的噪声被抑制到量子散粒噪声极限（SNL）以下，而另一分量的噪声相应增加，以满足量子不确定性原理。这种压缩是量子层面的噪声重构，直接影响光信号的量子统计特性。
混音中的 Compressor是经典信号处理工具，通过动态调整信号的增益来压缩动态范围。例如，当输入信号超过阈值时，压缩器按设定的比率（如 4:1）降低输出增益，从而减少信号峰值与平均值的差距，使音频更均衡。这是模拟或数字域的幅度调整，不涉及量子效应。

2. 技术实现：量子光学 vs 电子 / 算法

光学压缩（Squeeze）的实现依赖非线性光学元件（如光纤、光学参量振荡器）和量子态工程。例如，美国科罗拉多大学团队利用克尔效应在光纤中实现了 1 GHz 光频梳的幅度压缩，在 2.5 THz 带宽内噪声降低 3 dB。压缩过程需精确控制光场的相位和强度，涉及量子态的产生、操控和探测。
音频压缩器（Compressor）的实现通过模拟电路或数字算法实现。例如：
- 光学压缩器（Opto Compressor）利用 LED 和光敏电阻的光电耦合效应，根据输入信号强度动态调整增益；
- VCA 压缩器（Voltage-Controlled Amplifier）通过电压信号直接控制增益，具有透明、精准的特点；
- 数字压缩器则通过算法（如动态阈值检测、比例压缩）处理音频信号。

3. 应用目标：突破极限 vs 优化听感

光学压缩的目标是突破经典噪声极限，提升计量性能。例如：
- 在双光梳光谱中，压缩态光频梳使硫化氢气体浓度测定的信噪比提升 3 dB，测量速度加快两倍；
- 中红外量子关联光梳技术通过抑制散粒噪声，实现分子指纹谱的高精度测量，信噪比超越经典极限 2 dB。
音频压缩器的目标是优化音频动态范围，提升听感。例如：
- 控制人声或鼓组的音量波动，使声音更稳定、融合；
- 在母带处理中增加整体响度，避免信号削波失真；
- 通过 “软拐点”（Soft Knee）或 “硬拐点”（Hard Knee）调整，塑造不同的声音风格（如温暖、硬朗）。

4. 数学模型：量子算符 vs 动态函数

光学压缩的数学描述基于量子力学算符。例如，压缩态可通过压缩算符 \(S(r, \theta)\) 作用于真空态或相干态得到：\(|\psi\rangle = S(r, \theta) |0\rangle \quad \text{或} \quad |\alpha\rangle = S(r, \theta) D(\alpha) |0\rangle\)其中 r 为压缩幅度，\(\theta\) 为压缩角，描述噪声被抑制的方向。压缩态的正交分量涨落满足：\(\Delta X_1 \Delta X_2 \geq \frac{1}{4} \quad \text{（不确定性原理）}\)但某一分量的涨落可低于散粒噪声极限（如 \(\Delta X_1 < \frac{1}{2}\)）。
音频压缩器的数学模型基于动态增益函数。例如，压缩器的输入 - 输出关系可表示为：\(\text{输出电平} = \text{阈值} + \frac{\text{输入电平} - \text{阈值}}{\text{比率}} \quad \text{（当输入电平 > 阈值时）}\)压缩器通过调整阈值、比率、启动时间（Attack）和释放时间（Release）等参数，动态改变信号的增益曲线。

5. 术语起源：量子物理 vs 工程实践

Squeeze（压缩）的起源源于量子力学中对光场量子涨落的 “压缩” 描述。例如，1985 年 Caves 首次提出利用压缩态提升引力波探测灵敏度，随后这一概念被引入光学频率梳领域。
Compressor（压缩器）的起源源于音频工程中对信号动态范围的 “压缩” 需求。最早的模拟压缩器出现在 20 世纪 30 年代，用于广播和录音，以解决信号过载问题。

总结：本质差异的直观对比

维度	光学压缩（Squeeze）	音频压缩器（Compressor）
领域	量子光学、精密计量	音频工程、信号处理
对象	光场的量子涨落分布	音频信号的幅度动态范围
技术核心	非线性光学、量子态工程	模拟电路或数字算法
目标	突破噪声极限，提升测量精度	优化听感，避免失真
数学基础	量子算符、不确定性原理	动态增益函数、阈值控制
典型应用	分子光谱分析、引力波探测	人声处理、母带压缩、现场扩声

简言之，光学压缩是量子世界的噪声重构，而音频压缩是经典信号的动态优化。二者虽共享 “压缩” 之名，但技术路径和科学意义截然不同。

【为什么低不确定度和高精度要分开说？】

要理解差异，需先厘清计量学中 3 个易混淆的术语：

术语	核心含义	本质属性
准确度（Accuracy）	测量结果与 “真值” 的接近程度（反映系统误差，如仪器校准偏差、环境干扰）。	与 “真值” 的偏差
精度（Precision）	多次重复测量结果的 “离散程度”（反映随机误差，如散粒噪声、短期波动）。	结果的一致性
不确定度（Uncertainty）	对测量结果 “可能偏离真值的范围” 的量化评估（综合了系统误差 + 随机误差）。	可靠性的量化

【关于相干态所决定的量子散粒噪声极限】

第一步：先明确核心概念 —— 什么是 “相干态的量子散粒噪声极限（SNL）”

散粒噪声极限（Shot Noise Limit, SNL）不是 “技术不够好” 导致的噪声，而是光的量子粒子性带来的 “固有噪声天花板”，是量子力学层面的基本约束。

起源：光由光子组成，光子到达探测器的过程是随机的（类似雨滴落在地面的分布），这种 “光子计数的统计涨落” 就是散粒噪声。
数学规律：对于平均功率为P的光场，散粒噪声的功率波动\(\delta P\)满足\(\delta P \propto \sqrt{P}\)（这正是你最初看到的公式）。
相干态的特殊性：我们日常使用的激光（包括 A、B 方案中的光学频率梳）都属于相干态光场。量子力学证明：相干态的散粒噪声是 “最小的经典噪声”，也是经典光源（非量子调控光源）能达到的理论噪声下限—— 这就是 “相干态决定的 SNL”。

简单说：只要用的是相干态激光（频率梳），且探测过程没有改变光场的量子态，噪声就必然被 “钉死” 在 SNL，再怎么优化光路、提升仪器精度，也无法突破这个极限。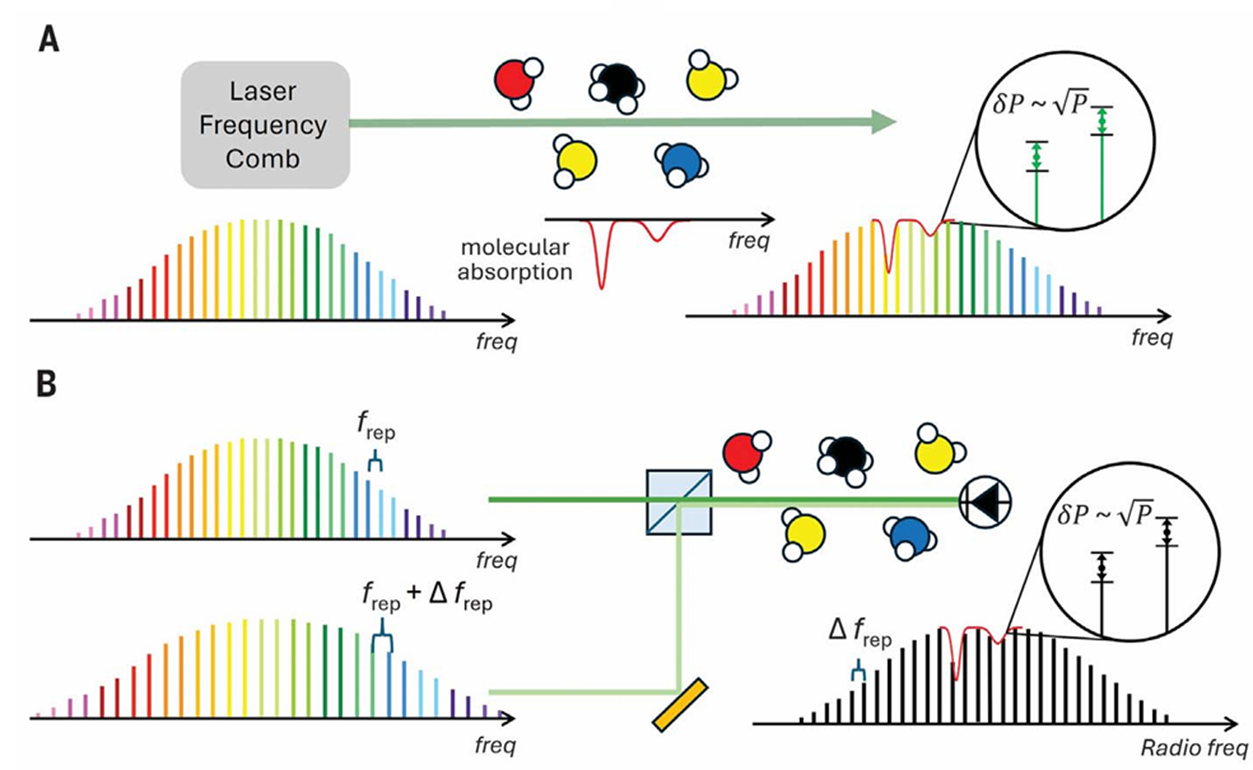

第二步：拆解方案 A 和 B—— 为何它们都逃不出 SNL 的束缚？

方案 A 和 B 的技术路径不同（光学域直接探测 vs 射频域拍频探测），但核心共性是 “均依赖相干态光场，且探测过程均为‘线性光学过程’”—— 这直接决定了它们无法突破 SNL。

1. 方案 A（直接光学吸收探测）：相干态的 “线性衰减” 不改变量子噪声特性

方案 A 的流程是：相干态频率梳 → 分子线性吸收 → 光学探测器接收。整个过程中，光场的量子态没有被 “重构”，仅发生了线性功率衰减。

分子吸收是 “线性过程”：分子只按比例吸收部分光子（形成吸收凹陷），但没有改变光子的统计分布 ——相干态经过线性吸收后，仍然是相干态。
探测器接收的仍是相干态：探测器测量的是衰减后相干态的光子流，其统计涨落依然遵循散粒噪声的规律（\(\delta P \sim \sqrt{P}\)）。
结论：方案 A 从光源到探测的全链路，都基于相干态的线性演化，噪声下限天然是 SNL，无法突破。

2. 方案 B（拍频探测）：“频率转换” 不改变噪声的量子本质

方案 B 的核心是 “光学 - 射频转换”，流程是：相干态信号梳 + 相干态参考梳 → 拍频（干涉） → 射频探测器接收。拍频是典型的线性光学干涉过程，同样不改变光场的量子态特性。

拍频的本质是 “频率平移”：参考梳与信号梳的频率差形成射频信号（如光学域 193 THz 的信号，与偏移 100 kHz 的参考梳拍频后，转换为 100 kHz 的射频信号）。但这个过程只是 “把光学信号的频率‘搬’到了射频域”，没有改变信号的噪声统计特性。
射频域的噪声仍是 “光学散粒噪声的平移”：射频信号的噪声，本质上是光学域相干态散粒噪声的 “镜像”—— 虽然频率降低了，便于电子学处理（如滤波、放大），但噪声的 “下限” 依然是光学域带来的 SNL。
结论：方案 B 只是 “换了个频率域处理信号”，没有改变光场的量子态（始终是相干态），也没有抑制散粒噪声的物理机制，因此同样被限制在 SNL。

第三步：关键总结 ——“达到极限” 的本质原因

方案 A 和 B 之所以达到 SNL，根本原因不是 “技术不够先进”，而是它们的设计逻辑完全基于 “经典相干态光场” 和 “线性光学过程”，这两条路径从根本上被量子力学的基本规律束缚：

光源的量子态限制：两者均使用相干态频率梳，而相干态的散粒噪声是经典光源的理论下限，无法通过经典手段消除。
探测过程的线性限制：无论是直接吸收（方案 A）还是拍频干涉（方案 B），都是线性光学过程 —— 线性过程只能 “传递或衰减信号 / 噪声”，不能 “重构光场的量子涨落”（而突破 SNL 恰恰需要重构量子涨落，如压缩态）。

打个通俗的比方：相干态光场的 SNL 就像 “一张纸的厚度”，方案 A 是 “直接用这张纸画画”，方案 B 是 “把这张纸复印到另一张薄纸上再画”—— 无论怎么操作，纸的基础厚度（SNL）都没变。只有换一张 “更薄的纸”（如压缩态光场），才能突破这个厚度极限。

延伸：如何突破 SNL？

正是因为 A、B 这类经典方案被 SNL 卡住，才有了原文提到的 “引入压缩态” 的思路：通过非线性光学过程（如光学参量振荡器）生成 “压缩态光场”—— 这种光场打破了相干态的量子涨落分布，能将某一正交分量（如幅度）的噪声抑制到 SNL 以下（代价是另一分量噪声增加，仍满足不确定性原理）。只有这种 “量子态调控”，才能真正突破相干态的固有噪声极限。

极化和非线性

χ⁽²⁾（二阶）和 χ⁽³⁾（三阶）非线性是非线性光学中最核心的两类非线性效应，其本质是光与介质相互作用时，介质的 “极化响应” 与入射光强的非线性关系（区别于线性光学中极化与光强成正比的关系）。二者的核心差异体现在响应阶数、依赖的介质特性、物理过程及工程实现难度上，这也直接解释了原文中 “选择更易获取的 χ⁽³⁾非线性” 的原因。

一、先明确基础：什么是 “极化率 χ⁽ⁿ⁾”？

当光（电磁波）入射到介质中时，会使介质中的原子 / 分子产生 “电极化”（电荷分布发生偏移，形成电偶极子），这种 “极化强度”（P）与入射光的电场强度（E）的关系，决定了介质的光学特性：

线性光学：极化强度仅与电场的一次方成正比，即 \(P = \chi^{(1)} E\)，其中 χ⁽¹⁾是 “一阶极化率”（对应折射、反射等经典现象）；
非线性光学：当入射光强足够高时（如激光），极化强度会出现与电场的高次方成正比的项，即：\(P = \chi^{(1)} E + \chi^{(2)} E^2 + \chi^{(3)} E^3 + \dots\)这里的 χ⁽²⁾（二阶）、χ⁽³⁾（三阶）就是 “高阶非线性极化率”，对应的项就是非线性效应的来源 ——阶数越高，非线性效应越弱，需要的入射光强越强。

二、χ⁽²⁾（二阶）非线性：依赖 “非中心对称介质” 的效应

1. 核心特点：介质必须 “非中心对称”

χ⁽²⁾非线性的产生有一个严格前提：介质不具有中心对称性（即空间反演后，介质的物理性质发生改变）。

举例：石英晶体（SiO₂，非中心对称）、铌酸锂（LiNbO₃，常用非线性晶体）、磷酸二氢钾（KDP）等；
反例：玻璃、普通光纤（SiO₂，中心对称结构）、水等 —— 这类介质的 χ⁽²⁾=0，无法产生二阶非线性效应。

这是因为中心对称介质中，“电场 E 和 - E 产生的极化响应完全相同”，而 \(E^2\) 项在 E 和 - E 下结果一致，会被介质的对称性 “抵消”，导致二阶极化项消失。

2. 典型物理过程（与压缩光相关）

χ⁽²⁾非线性会引发 “频率转换” 类效应，是生成宽频压缩光的经典途径：

光学参量振荡（OPO）：入射的强激光（泵浦光）通过 χ⁽²⁾晶体，分裂为两束频率更低的光（信号光和闲频光），且信号光与闲频光存在量子关联 —— 通过调控 OPO，可生成覆盖几十到几百 THz 带宽的压缩态光场（这就是原文 “较宽光学带宽内实现压缩” 的来源）。
倍频（SHG）：泵浦光通过 χ⁽²⁾晶体后，产生频率为泵浦光 2 倍的光（如 1064 nm 激光倍频为 532 nm 绿光），虽不直接生成压缩光，但可作为 OPO 的泵浦源。
和频 / 差频：两束不同频率的光（E₁=ω₁，E₂=ω₂）入射晶体，产生频率为 ω₁+ω₂（和频）或 |ω₁-ω₂|（差频）的光。

3. 优势与局限

优势：非线性效应相对较强（比 χ⁽³⁾容易激发），可生成宽带宽的压缩光（如 OPO 生成的压缩光带宽能匹配光学频率梳的覆盖范围）；
局限：介质获取和使用门槛高 —— 非线性晶体需精确切割（保证相位匹配）、镀膜（减少反射损耗），且对温度、振动极敏感（相位失配会快速削弱效应），系统集成性差、成本高。

三、χ⁽³⁾（三阶）非线性：“中心对称 / 非对称介质均可产生” 的效应

1. 核心特点：无介质对称性限制

χ⁽³⁾非线性的产生不依赖介质的中心对称性—— 无论是中心对称还是非中心对称介质，只要光强足够高，都能激发三阶非线性效应。

举例：普通单模光纤、高非线性光纤（HNLF，中心对称 SiO₂结构）、半导体材料（如 GaAs）、玻璃、甚至空气等；
原因：三阶项 \(E^3\) 在 E 和 - E 下符号相反，不会被中心对称介质抵消，因此所有介质都有 χ⁽³⁾（只是大小不同）。

2. 典型物理过程（与压缩光相关）

χ⁽³⁾非线性主要引发 “自作用” 或 “互作用” 类效应，是光纤中生成压缩光的主流途径：

克尔效应（Kerr Effect）：光自身的电场改变介质的折射率（折射率随光强变化：\(n = n_0 + n_2 I\)，n₂是克尔系数），导致不同频率的光产生相位耦合 —— 在光纤中，克尔效应会引发 “自相位调制（SPM）” 和 “交叉相位调制（XPM）”，通过调控光强和光纤长度，可实现对光学频率梳的幅度压缩（这是原文方案的核心）。
四波混频（FWM）：两束泵浦光（ω₁、ω₂）入射介质，通过 χ⁽³⁾非线性产生两束新光（ω₃=ω₁+ω₂-ω₄，ω₄），新光与泵浦光存在量子关联，可用于生成多频梳模的压缩光。
拉曼散射（Raman Scattering）：光与介质分子振动相互作用，通过 χ⁽³⁾非线性产生频移的散射光，可用于增强特定梳模的非线性响应。

3. 优势与局限

优势：介质 “极易获取”—— 光纤是最常见的 χ⁽³⁾介质，成本低、柔性好、易集成（可直接接入光学频率梳系统），且对环境扰动的容忍度高于晶体；
局限：非线性效应较弱（比 χ⁽³⁾弱 1-2 个量级），需要更高的入射光强（通常是毫瓦至瓦级）才能激发；且光纤的非线性带宽受色散限制，宽频压缩的难度略高于 χ⁽²⁾晶体。

四、核心对比：χ⁽²⁾ vs χ⁽³⁾非线性（表格总结）

维度	χ⁽²⁾（二阶）非线性	χ⁽³⁾（三阶）非线性
介质对称性要求	必须非中心对称（如铌酸锂晶体）	无要求（中心 / 非中心对称均可，如光纤、玻璃）
典型介质	非线性晶体（LiNbO₃、KDP）、非对称半导体	光纤（HNLF）、玻璃、半导体、空气
非线性强度	较强（易激发，低光强即可）	较弱（难激发，需高光强）
典型物理过程	光学参量振荡（OPO）、倍频、和频 / 差频	克尔效应、四波混频、拉曼散射
压缩光带宽能力	较宽（可覆盖数百 THz）	中等（受介质色散限制，光纤中可达数十 THz）
工程实现难度	高（晶体需精确对准、控温，集成性差）	低（光纤易获取、易集成，环境容忍度高）
成本	高（特种晶体价格昂贵）	低（光纤等介质廉价）

五、结合原文语境：为什么选择 χ⁽³⁾非线性？

原文明确提到 “尽管 χ⁽²⁾可实现宽频压缩，但选择更易获取的 χ⁽³⁾”，核心原因就是χ⁽³⁾的 “工程实用性” 远高于 χ⁽²⁾：

介质易获取：无需依赖昂贵的特种晶体，普通高非线性光纤（HNLF）即可实现，成本仅为晶体的 1/10-1/100；
系统易集成：光纤可直接与光学频率梳的光路对接（无需复杂的晶体对准结构），且抗振动、抗温度扰动能力更强，适合搭建稳定的光谱探测系统；
适配实用功率：原文目标是 “微瓦至毫瓦级实用功率”，χ⁽³⁾虽需高光强，但现代光纤放大器可轻松实现毫瓦级泵浦，无需极端实验条件。

简言之，χ⁽²⁾是 “性能优先”（宽带宽），但 χ⁽³⁾是 “实用优先”（易获取、低成本、易集成）—— 对于追求 “简便方案” 的研究而言，χ⁽³⁾非线性是更现实的选择。

【什么玩意，孤子？】

“孤子压缩技术”（Soliton Squeezing Technology）是一种利用光学孤子的特殊稳定性和非线性特性，实现光场量子涨落抑制（即量子压缩）的前沿技术。它结合了 “光学孤子” 的经典波形稳定性与 “量子压缩” 的噪声调控能力，尤其在光学频率梳、精密计量、量子通信等领域具有重要应用潜力。

一、先明确两个核心基础概念

要理解孤子压缩技术，需先厘清 “光学孤子” 和 “量子压缩” 的关联：

光学孤子（Optical Soliton）：是一种在传播过程中形状、幅度、速度保持不变的特殊光脉冲 / 光束。其本质是介质的非线性效应（如 χ⁽³⁾克尔效应）与色散效应（不同频率光传播速度不同）相互抵消的平衡态 —— 非线性使脉冲自聚焦（幅度增强处折射率升高，压缩脉冲），色散使脉冲展宽，二者抵消后形成 “自稳定” 的孤子。举例：光纤中的 “时间孤子”（脉冲在时间维度上稳定传播）、光晶格中的 “空间孤子”（光束在空间维度上不发散）。
量子压缩（Quantum Squeezing）：指通过调控光场的量子态，将某一正交分量（如幅度、相位）的噪声抑制到散粒噪声极限（SNL）以下（代价是另一分量噪声增加，满足量子不确定性原理），核心目标是突破经典相干态的噪声天花板。

二、孤子压缩技术的核心原理：“孤子的非线性关联” 驱动量子压缩

孤子压缩技术的本质是：利用孤子形成过程中强烈的非线性相互作用（主要是 χ⁽³⁾克尔效应），使孤子内的光子产生量子关联，进而重构光场的量子涨落分布，实现压缩。

具体过程可拆解为 3 步：

1. 孤子的形成：构建非线性 - 色散平衡态

通过高功率激光泵浦非线性介质（如高非线性光纤、微谐振器），使入射光的克尔非线性效应（χ⁽³⁾）与介质色散达到精确平衡，形成稳定的光学孤子。

例如：在微谐振器中，泵浦光激发的 “耗散孤子”（Dissipative Soliton）—— 不仅平衡了非线性与色散，还平衡了增益与损耗，能长期稳定存在，是生成孤子频率梳的核心。

2. 孤子内的量子关联：光子间的 “协同作用”

孤子并非孤立的光子流，其内部光子因强烈的非线性耦合（如交叉相位调制、四波混频）产生量子纠缠或经典关联—— 这种关联打破了相干态中光子的随机统计分布，使光子的到达时间 / 幅度呈现 “协同性”。

通俗理解：相干态的光子像 “随机下落的雨滴”（噪声随机），而孤子中的光子像 “整齐列队的士兵”（部分维度的涨落被同步抑制）。

3. 量子涨落的重构：实现压缩

孤子内的量子关联直接导致光场量子涨落的重新分配：

若调控孤子的形成条件（如泵浦功率、介质色散、孤子阶数），可使孤子光场的幅度正交分量噪声被抑制（幅度压缩），或相位正交分量噪声被抑制（相位压缩）。
例如：光纤中传播的时间孤子，其幅度涨落因克尔非线性的 “自稳定作用” 被抑制，可实现 1-3 dB 的幅度压缩；微谐振器中的孤子梳，通过优化谐振腔参数，能实现多梳模的同步压缩。

三、孤子压缩技术的关键特点（与传统压缩方案对比）

相较于传统的 “光学参量振荡器（OPO，基于 χ⁽²⁾非线性）压缩”，孤子压缩技术具有 3 个核心优势：

对比维度	传统 OPO 压缩（χ⁽²⁾）	孤子压缩技术（χ⁽³⁾）
介质要求	需非中心对称晶体（如 LiNbO₃），成本高、易损坏	中心对称介质即可（如光纤、微谐振器），易获取、易集成
压缩带宽	较宽（但受晶体带宽限制）	极宽（孤子频率梳可覆盖 THz 量级，支持多梳模压缩）
稳定性	对温度、振动敏感，需精密控温	孤子自身具有 “自稳定性”，系统更鲁棒
与频率梳兼容性	需额外耦合到频率梳，集成复杂	可直接生成 “压缩孤子频率梳”，一步实现梳状光谱与压缩
典型压缩度	较高（可达 10 dB 以上）	中等（目前实验可达 3-6 dB，仍在提升）

四、主要应用场景（结合光学频率梳与计量需求）

孤子压缩技术的核心价值在于 **“宽频、稳定、易集成的量子压缩光源”**，尤其适配光学频率梳的计量需求：

量子增强双梳光谱：生成 “压缩孤子频率梳”，直接应用于模式分辨双梳光谱（DCS）—— 通过抑制梳模的幅度噪声，突破散粒噪声极限，提升分子吸收谱的信噪比（SNR）和测量精度，可用于痕量气体检测、生物分子指纹分析。
精密时间 / 频率计量：孤子压缩光场的相位噪声可被抑制，用于优化光学原子钟的 “光钟激光” 稳定性，或提升微波光子学中 “光 - 电频率转换” 的精度。
量子通信与量子计算：孤子压缩频率梳的多梳模特性，可作为 “多通道量子资源”—— 每个梳模对应一个量子比特，用于构建高维度量子通信系统或集成化量子计算芯片。

五、当前研究进展与挑战

1. 研究突破

2021 年，美国国家标准与技术研究院（NIST）团队在高非线性光纤中实现了1 GHz 重复频率的孤子压缩频率梳，压缩度达 2.8 dB，成功应用于分子光谱探测；
2023 年，中国科学技术大学团队通过微谐振器生成 “耗散孤子压缩梳”，实现了50 THz 带宽内的多模同步压缩，为宽频光谱应用奠定基础。

2. 核心挑战

压缩度提升：目前孤子压缩度（3-6 dB）低于 OPO 方案（10 dB 以上），需优化非线性介质（如低损耗氮化硅微谐振器）和孤子调控策略；
损耗控制：光纤 / 微谐振器的传输损耗会削弱量子关联，需发展超低损耗介质；
室温稳定运行：部分孤子压缩系统仍需低温环境（抑制热噪声），室温下的长期稳定性待突破。

总结：孤子压缩技术的本质

孤子压缩技术是“经典孤子的自稳定特性” 与 “量子压缩的噪声调控目标” 的结合—— 通过非线性与色散的平衡构建稳定孤子，再利用孤子内的量子关联实现噪声抑制。它解决了传统压缩方案 “集成难、带宽窄” 的痛点，是推动光学频率梳从 “经典计量” 迈向 “量子增强计量” 的关键技术之一。

【激光线宽的定义与观测方式】

1. 激光线宽的含义

激光线宽（Laser Linewidth）是指激光光谱的半高全宽（FWHM, Full Width at Half Maximum），即光谱强度降至峰值一半时对应的频率或波长范围。它反映了激光的单色性和相干性：线宽越窄，激光频率越单一，相干时间越长（相干性越高）。

例如，若激光峰值光强为 100，线宽是光强为 50 时两个频率点的差值（类似电子学中的 “带宽”，但针对光信号）。

2. 观测域的选择：线性域 vs 对数域

（1）线性域（光强 - 频率 / 波长呈线性刻度）

必要性：线宽的标准定义（FWHM）要求光强以线性比例（如 0% 到 100% 峰值）展示。在线性域中，“半高” 直接对应光强为峰值的 50%，能准确测量 FWHM 的真实宽度。
适用场景：所有需要严格符合 FWHM 定义的场景，如评估激光的相干性、谐振腔品质因数（Q 值）等。

（2）对数域（光强取对数，如 dB 刻度）

可行性：对数域可用于辅助分析，但需明确标注刻度类型，否则会混淆线宽的定义：
- 若在对数域测量 “半高”，实际是光强为峰值的 1/10（-10dB）或 1/2（-3dB），与线性域的 “50% 峰值” 不同。
- 对数域的优势是能压缩高功率部分、拉伸低功率部分，便于观察弱旁瓣或宽谱范围（如激光的边模抑制比）。
特殊场景：
- 测量窄线宽激光器时，常采用 **“-20dB 处的宽度”** 间接估算线宽（如自外差法）。此时需说明是 “-20dB 宽度”，而非传统 FWHM。

3. 总结

标准线宽（FWHM）必须在线性域测量：这是线宽定义的核心要求，确保 “半高” 对应 50% 峰值光强。
对数域可用于辅助分析：但需明确标注刻度类型（如 “-3dB 宽度”“-20dB 宽度”），避免与标准 FWHM 混淆。

例如，某激光器在线性域的 FWHM 为 10 MHz，而在对数域（-20dB）的宽度可能为 50 MHz，两者物理意义不同，需根据需求选择观测方式。

【这个CEO不是那个CEO】

载波 - 包络偏置频率（Carrier-Envelope Offset Frequency，简称 fₒₑₒ 或 “偏频”）是超短脉冲激光（尤其是飞秒激光） 特有的核心参数，本质上描述了激光脉冲的 “快振荡载波” 与 “慢变化包络” 之间的相位关系随时间的变化率。要理解它，需要先从超短脉冲的结构入手。

一、先搞懂：超短脉冲的 “载波” 与 “包络”

飞秒激光不是连续光，而是一串极短的脉冲序列（脉冲宽度通常为 10⁻¹⁵~10⁻¹² 秒）。每个脉冲的光场由两部分构成：

包络（Envelope）：脉冲的 “轮廓”，决定了脉冲的强度分布（比如高斯型轮廓），变化速度较慢（对应脉冲的持续时间）。
载波（Carrier）：在包络内部快速振荡的光波，频率极高（对应光的颜色，比如近红外光的载波频率约为 10¹⁴ Hz），类似 “轮廓里的涟漪”。

下图是直观类比：包络像 “海浪的浪头”，载波像 “浪头里的高频振动”。

二、fₒₑₒ的本质：载波与包络的 “相位偏移率”

1. 核心矛盾：“包络重复” 与 “载波重复” 的不匹配

飞秒激光的脉冲序列有两个关键频率：

包络重复频率（fᵣ）：脉冲串中相邻两个脉冲包络的峰值间隔对应的频率（比如 100 MHz，即每秒产生 1 亿个脉冲）。
载波频率（f꜀）：包络内部载波的振荡频率（比如近红外光 f꜀≈3×10¹⁴ Hz）。

理想情况下，若每个脉冲的载波都 “对齐” 包络（比如载波峰值刚好落在包络峰值上），则相邻脉冲的载波相位一致。但实际中，载波的振荡周期与包络的重复周期并非整数倍关系—— 假设每个包络周期内有 N 个载波振荡，剩余了一小段 “相位偏移”，这个偏移会在每个脉冲中累积。

2. fₒₑₒ的定义：累积偏移的 “频率化表达”

这种相邻脉冲间的载波 - 包络相位差（CEP） 会随时间线性变化，其变化率就是 fₒₑₒ。数学上可表示为：fₒₑₒ = f꜀ - N·fᵣ其中：

N 是 “每个包络周期内的载波振荡整数次”（比如 N≈3000，对应 f꜀=3×10¹⁴ Hz、fᵣ=100 MHz）；
fₒₑₒ就是 “载波频率” 与 “包络重复频率整数倍” 的差值，通常在 10 kHz~100 MHz 之间（远低于 f꜀和 fᵣ）。

三、通俗理解：fₒₑₒ是载波的 “滑动速度”

可以把脉冲包络想象成一个 “移动的窗框”，载波是窗框里 “快速转动的齿轮”：

若 fₒₑₒ=0：齿轮每转 N 圈，窗框刚好移动一次，齿轮的 “齿尖” 始终对准窗框中心（CEP 稳定，载波与包络完全同步）。
若 fₒₑₒ≠0：齿轮每转 N 圈后，还差一小段才对齐窗框，下次脉冲时齿轮的位置就 “滑” 了一点 ——fₒₑₒ越大，滑动越快，直到齿轮位置循环一周（对应 CEP 的 “缠绕”）。

四、为什么 fₒₑₒ重要？

fₒₑₒ直接决定了超短脉冲的载波 - 包络相位（CEP）稳定性，而 CEP 是强场激光物理、阿秒科学等领域的 “核心开关”：

例如，高次谐波生成（阿秒脉冲的来源） 中，电子在激光场中的加速 / 电离轨迹完全由 CEP 决定 —— 只有锁定 fₒₑₒ（让 fₒₑₒ=0 或稳定在固定值），才能产生稳定的阿秒脉冲。
再如，量子调控、激光核聚变等场景，也需要精确控制 CEP，而 fₒₑₒ是调控 CEP 的 “抓手”。

总结

概念	核心含义
载波 - 包络	超短脉冲的 “快振荡内核” 与 “慢变化轮廓”
fₒₑₒ（偏频）	载波频率与包络重复频率整数倍的差值，反映载波相对于包络的 “滑动速率”
物理意义	决定 CEP 稳定性，是超短脉冲激光 “高精密应用” 的关键参数

简单说：fₒₑₒ就是超短脉冲里 “快波” 和 “慢波” 的 “节奏差”，这个差值虽小，却能决定激光在极端物理场景中的性能。

【怎么稳定fceo？】

稳定载波 - 包络偏置频率f_ceo是超短脉冲激光技术的核心挑战之一，其稳定性直接影响到阿秒科学、光学频率梳应用（如光学原子钟）以及精密光谱学等领域的性能。以下是目前主流的稳定技术及最新进展：

一、基础技术框架：自参考干涉与锁相环（PLL）

f-2f 自参考干涉法
- 原理：将激光光谱展宽至至少一个倍频程（如通过高非线性光纤或纳米光子波导），分离低频部分并倍频，与高频部分拍频得到f_ceo信号。
- 反馈控制：通过锁相环（PLL）将 f_ceo 信号与参考射频源（如 10 MHz 晶振）比较，产生误差信号反馈至激光器的泵浦电流、腔长或相位调制器，实现闭环锁定。
- 优势：技术成熟，可达到 \(10^{-17}\) 量级的秒级稳定度。
- 局限：传统方案需脉冲能量 >1 nJ，限制了其在低功率或高重复频率（如 GHz）激光器中的应用。

二、前沿技术突破

1. 纳米光子波导技术（COSMO 模块）

技术革新：Octave Photonics 开发的 COSMO 模块采用硅基纳米光子波导，将超连续谱产生与二次谐波生成集成在芯片上，使 f_ceo 检测所需的脉冲能量降至 <200 pJ（平均功率 <200 mW），信噪比>35 dB。
应用案例：
- 与 Menhir Photonics 的 1 GHz 飞秒激光器结合，在 1000 秒内实现 \(10^{-20}\) 量级的频率稳定度。
- 简化系统搭建：模块通过标准光纤连接器连接，无需复杂光路对准，可在几分钟内完成 f_ceo 锁定。

2. 前置反馈锁定技术

原理：在激光输出路径中插入声光调制移频器（AOFS），直接将 f_ceo 误差信号调制到激光频率上，实时补偿相位漂移。
优势：
- 高频噪声抑制：无 PID 滤波环节，带宽可达 10 GHz，积分相位噪声（1 Hz-1 MHz）低至 79.3 mrad，比传统 PLL 降低 70%。
- 兼容性强：不影响激光器原有结构，适用于全固态 Yb:CYA 等多种激光系统。

3. 时域外差干涉法

原理：利用空间延迟线使脉冲序列自干涉，提取不同光谱区域的外差相位差，间接锁定 f_ceo 。
特点：
- 无需倍频程光谱，适用于窄谱激光器。
- 稳定度中等（秒级相对阿伦方差 \(10^{-9}\)），但成本较低且动态响应快。

三、系统级优化策略

环境噪声隔离
- 采用保偏光纤（PMF）和恒温封装，减少温度波动和机械振动对光路的影响。
- 在高频应用中（如 1 GHz），使用超低噪声射频源（如 Vescent SLICE-OPL）提升反馈精度。
多参数协同锁定
- 同时锁定重复频率 f_rep和 f_ceo ，例如：
  - 通过 PID 电路分别控制泵浦电流（ f_ceo ）和腔长（ f_rep）。
  - 使用 Moku:Pro 等多功能仪器并行处理两个闭环反馈。
参考源升级
- 将 f_ceo锁定至超稳激光（如锁定到 972 nm 超稳 F-P 腔），可将长期稳定度提升至 \(10^{-18}\) 量级，适用于光学原子钟。

四、典型应用场景与方案选择

应用场景	推荐技术方案	稳定度指标（秒级）
阿秒脉冲产生	前置反馈锁定（AOFS）+ 超稳激光参考	\(<10^{-18}\)
1 GHz 高频光频梳	COSMO 模块 + Vescent SLICE-OPL	\(10^{-20}\)
低成本实验室演示	时域外差干涉法 + 射频源（如 Agilent 8648C）	\(10^{-9}\)
工业级高精度计量	传统 f-2f + 保偏光纤系统 + 恒温控制	\(10^{-17}\)

五、最新进展与趋势

片上集成化：基于氮化镓（GaN）等材料的光子芯片实现片上超连续谱展宽和 f-2f 自参考，功耗低至微瓦级。
智能化反馈：机器学习算法优化 PID 参数，动态适应环境变化，提升长期稳定性。
多自由度控制：结合电光调制器（EOM）和 PZT，同时补偿相位和幅度噪声，实现全噪声抑制。

通过上述技术的组合与优化，目前 f_ceo 稳定度已突破 \(10^{-20}\) 量级，为下一代精密测量技术奠定了基础。具体方案需根据应用需求（如稳定度、成本、系统复杂度）综合选择。

【拍频是相加还是相乘？】

理解 “为什么相乘能产生携带信息的拍频信号”，需要从 **“光的波动本质”和“探测器的工作原理”** 两个层面逐步拆解，核心是：拍频信号来自 “两束光的频率差”，而探测器的 “平方律响应”（对应数学上的 “相乘”）是提取这个频率差的关键。

一、先明确：什么是 “拍频”？

拍频（Beat Frequency）是两个频率接近的波动叠加后，形成的 “强度周期性变化” 现象，本质是 “频率差” 的体现。

举个生活中的例子：

两个音叉分别发出频率为 440Hz 和 442Hz 的声音（频率接近），人耳听到的不是两个高频声音，而是 “强弱交替的嗡嗡声”，其强弱变化的频率是 2Hz（442-440）—— 这就是 “声拍频”，频率等于两个原始频率的差。

光的拍频原理完全相同：两束频率接近的光叠加后，光强会以 “两光频率差” 的频率周期性变化，这个变化频率就是 “光拍频”。

二、为什么 “电场相加” 得不到可测的拍频信号？

光作为电磁波，两束光相遇时，电场确实是 “相加” 的（波动叠加原理），但这个 “相加” 的结果是高频的，探测器根本 “看不懂”。

具体来说：设两束光的电场为（简化为标量，忽略偏振）：\(E_1(t) = A_1 \cos(2\pi f_1 t)\)\(E_2(t) = A_2 \cos(2\pi f_2 t)\)其中 \(f_1、f_2\) 是光的频率（约 \(10^{14}\ \text{Hz}\)，远高于电子设备的响应速度），\(A_1、A_2\) 是振幅。

叠加后的总电场是：\(E_{\text{总}}(t) = E_1(t) + E_2(t) = A_1 \cos(2\pi f_1 t) + A_2 \cos(2\pi f_2 t)\)

这个总电场的频率仍是 \(10^{14}\ \text{Hz}\) 量级（光学高频），而任何电子探测器（如光电二极管）的响应速度都远低于这个频率（最快的探测器也只能响应到 \(10^{11}\ \text{Hz}\) 左右），无法直接 “跟随” 这么快的变化，只能测量其 “平均强度”—— 因此，直接对电场 “相加” 的结果进行探测，会丢失所有高频信息，更得不到拍频。

三、为什么 “平方律探测”（对应数学上的 “相乘”）能得到拍频信号？

光探测器的核心特性是 “平方律响应”：它输出的电信号强度与 “光的强度” 成正比，而光强与电场的平方成正比（\(I \propto |E|^2\)）。

对总电场平方后，奇迹发生了：高频成分被 “过滤”，低频的拍频成分被提取出来。

具体推导：光强 \(I(t) \propto |E_{\text{总}}(t)|^2 = (E_1 + E_2)^2\)，展开后：\(\begin{align*} I(t) &\propto E_1^2 + E_2^2 + 2E_1E_2 \\ &= A_1^2 \cos^2(2\pi f_1 t) + A_2^2 \cos^2(2\pi f_2 t) + 2A_1A_2 \cos(2\pi f_1 t)\cos(2\pi f_2 t) \end{align*}\)

用三角函数公式化简每一项：

第一项 \(\cos^2(2\pi f_1 t) = \frac{1 + \cos(4\pi f_1 t)}{2}\)，包含 “直流成分”（1/2）和 “2 倍频高频成分”（\(\cos(4\pi f_1 t)\)）；
第二项同理，也包含直流成分和 2 倍频高频成分；
第三项（交叉项）用积化和差公式：\(2\cos(2\pi f_1 t)\cos(2\pi f_2 t) = \cos[2\pi(f_1 + f_2)t] + \cos[2\pi(f_1 - f_2)t]\)

四、关键：只有 “频率差成分” 能被探测器捕捉

上述展开式中，存在三类成分：

直流成分：不随时间变化（来自 \(\cos^2\) 中的 1/2 项）；
高频成分：频率为 \(2f_1、2f_2、f_1 + f_2\)（都是 \(10^{14}\ \text{Hz}\) 量级，探测器无法响应）；
低频成分：频率为 \(|f_1 - f_2|\)（即两光的频率差，若 \(f_1 \approx f_2\)，这个差可以是 \(10^3 \sim 10^6\ \text{Hz}\)，属于射频范围，探测器可响应）。

探测器会 “过滤掉所有高频成分”（只保留低频和直流），因此最终输出的电信号主要由 “频率差成分” 决定：\(I_{\text{输出}}(t) \propto \text{直流项} + \cos[2\pi(f_1 - f_2)t]\)

这个 “\(\cos[2\pi(f_1 - f_2)t]\)” 就是我们需要的拍频信号，其频率等于两束光的频率差 \(|f_1 - f_2|\)，携带了两光频率差的信息。

五、代码中 “相乘” 的意义：直接提取拍频核心项

代码中 beat_signal = comb1 .* comb2 是对上述物理过程的简化模拟：

comb1 和 comb2 对应两束光的电场 \(E_1(t)\) 和 \(E_2(t)\)；
它们的乘积 \(E_1(t) \cdot E_2(t)\) 直接对应展开式中的 “交叉项核心”（忽略系数后，就是 \(\cos(2\pi f_1 t)\cos(2\pi f_2 t)\)）；
这个乘积经过三角函数变换后，直接包含拍频信号 \(\cos[2\pi(f_1 - f_2)t]\)，省去了计算平方和过滤高频的步骤（因为高频成分在仿真中不影响对拍频的观察）。