机器学习——决策树详解

一、决策树简介

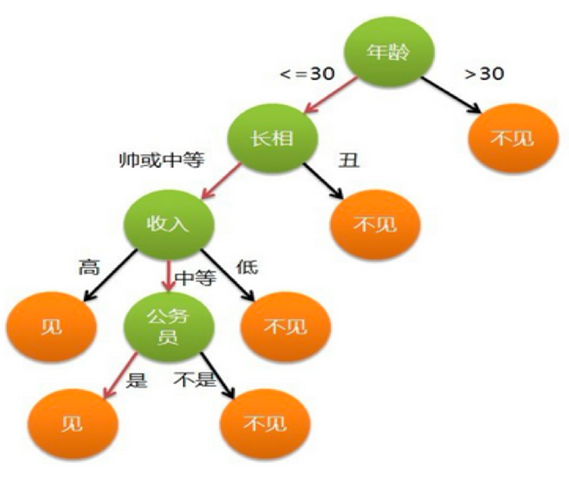
1. 定义：决策树是一种树形结果，树中每个内部节点表示一个特征上的判断，每个分支代表一个判断结果的输出每个叶子节点代表一种分类结果
2. 决策树建立过程：

• 特征选择：选取有较强分类能力的特征
• 决策树生成：根据选择的特征生成决策树
• 决策树也容易过拟合，采用剪枝的方法环节过拟合

二、ID3树

1. 定义：一种基于信息增益构建的决策树
2. 信息熵（Entropy）：信息论中代表随机变量不确定度的度量

• 熵越大，数据的不确定性度越高，信息越多
• 熵越小，数据的不确定性越低
• 计算公式：$\mathsf{H}(x)=-{\sum }_{i=0}^{n}P(x_i){\log }_{2}P(x_i)$
  • 其中$P(x_i)$表示数据中类别出现的概率，$H(x)$表示信息的信息熵值

计算数据$\alpha (ABCDEFGH)$信息熵，其中每个字符出现概率均为$\frac{1}{8}$：$$\mathsf{H}(\alpha )=-\sum _{i=0}^{n}P(x_i){\log }_{2}P(x_i)=(-\frac{1}{8}{\log }_2\frac{1}{8})\ast 8=3$$
计算数据$\beta (AAAABBCD)$信息熵：
$$\mathrm{H}(\mathrm{B})=-\sum _{i=0}^{n}P(x_i){\log }_{2}P(x_i)=(-\frac{1}{2}{\log }_2\frac{1}{2})+(-\frac{1}{4}{\log }_2\frac{1}{4})+(-\frac{1}{8}{\log }_2\frac{1}{8})\ast 2=\frac{1}{2}\ast 1+\frac{1}{4}\ast 2+\frac{1}{8}\ast 3\ast 2=1.75$$

3. 信息增益：特征a对训练数据集D的信息增益$g(D,a)$，定义为集合D的熵$H(D)$与特征a给定条件下D的熵$H(D|a)$之差

• 计算公式：$g(H,A)=H(D)-H(D|A)，信息增益=熵-条件熵$
• 条件熵：$$\mathrm{H}(\mathrm{D}\mid \mathrm{A})=\sum _{v=1}^n\frac{D^V}{D}\mathrm{H}(D^V)=\sum _{v=1}^n\frac{D^V}{D}\sum _{\mathrm{k}=1}^{\mathrm{k}}\frac{C^{kV}}{D^V}log\frac{C^{kV}}{D^V}$$

已知6个样本，根据特征A：
$\alpha$部分对应的目标值为：AAAB
$\beta$部分对应的目标值为：BB

• 条件熵为$\alpha$：$(-\frac{3}{4}lo{g}_2\frac{3}{4})+(-\frac{1}{4}lo{g}_2\frac{1}{4})=0.81$
• 条件熵为$\beta$：$(-\frac{2}{2}lo{g}_2\frac{2}{2})=0$
• 条件熵：$\alpha$部分占据$\frac{4}{6}$，$\beta$部分占据$\frac{2}{6}$，则$\frac{4}{6}\cdot 0.81+\frac{2}{6}\cdot 0=0.54$
• 熵：$(-\frac{3}{6}lo{g}_2\frac{3}{6})+(-\frac{3}{6}lo{g}_2\frac{3}{6})=1$
• 信息增益：$熵-条件熵=1-0.54=0.46$

4. ID3决策树构建流程：

• 计算每个特征的信息增益
• 使用信息增益最大的特征将数据集拆分为子集
• 使用该特征（信息增益最大的特征）作为决策树的一个节点
• 使用剩余特征重复以上过程

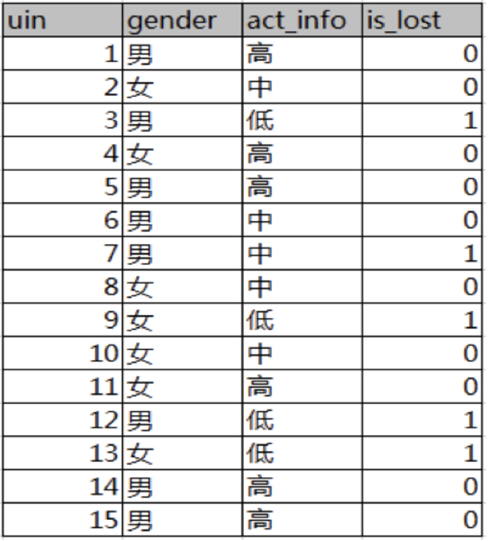
已知某一论坛客户流失率数据，要求考察性别、活跃度特征哪个特征对流失率大

• 计算熵：$\mathrm{H}(\mathrm{D})=(-\frac{5}{15}{\log }_2\frac{5}{15})+(-\frac{10}{15}{\log }_2\frac{10}{15})=0.9812$
• 计算性别条件熵：$H(D，性别)=(\frac{8}{15})(-\frac{3}{8}{\log }_2\frac{3}{8}-\frac{5}{8}{\log }_2\frac{5}{8})+(\frac{7}{15})(-\frac{2}{7}{\log }_2\frac{2}{7}-\frac{5}{7}{\log }_2\frac{5}{7})=0.9748$
• 计算性别信息增益：$g(D,\alpha )=H(D)-H(D|\alpha )=0.9812-0.9748=0.0064$
• 计算活跃度条件熵：$H(D，活跃度)=(\frac{6}{15})(0)+(\frac{5}{15})(-\frac{1}{5}{\log }_2\frac{1}{5}-\frac{4}{5}{\log }_2\frac{4}{5})+(\frac{4}{15})=0.3036$
• 计算活跃度信息增益：$g(D,\alpha )=H(D)-H(D|\alpha )=0.9812-0.3036=0.6776$
• 结论：活跃度的信息增益比性别的信息增益大，对用户流失的影响比性别大

三、C4.5树

我们发现上述例子中，若将uin也作为一个特征，那么根据ID3的公式，uin的信息增益会很大，因此ID3树的不足在于其更偏向于选择种类多的特征作为分裂依据，因此C4.5树将信息增益改为了信息增益率

1. $信息增益率=\frac{信息增益}{特征熵}$
2. 本质：

• 特征的信息增益 / 特征的内在信息
• 相当于对信息增益进行修正，增加一个惩罚系数
• 特征取值个数较多时，惩罚系数较小；特征取值个数较少时，惩罚系数较大
• 惩罚系数：数据集D以特征a作为随机变量的熵的倒数

现在希望求特征a、b的信息增益率

• 对于特征a的信息增益率：
  • 信息增益：$(-\frac{3}{6}{\log }_2\frac{3}{6}-\frac{3}{6}{\log }_2\frac{3}{6})-(\frac{4}{6}\cdot (-\frac{3}{4}{\log }_2\frac{3}{4}-\frac{1}{4}{\log }_2\frac{1}{4})-\frac{2}{6}\cdot (-0))=1-0.54=0.46$
  • 信息熵：$-\frac{4}{6}{\log }_2\frac{4}{6}-\frac{2}{6}{\log }_2\frac{2}{6}=0.92$
  • 信息增益率：$信息增益/信息熵=0.46/0.92=0.5$
• 特征b的信息增益率：
  • 信息增益：$(-\frac{3}{6}{\log }_2\frac{3}{6}-\frac{3}{6}{\log }_2\frac{3}{6})-6\cdot 0=1$
  • 信息熵：$-\frac{1}{6}{\log }_2\frac{1}{6}\cdot 6=2.58$ * 信息增益率：$信息增益/信息熵=1/2.58=0.39$

四、CART决策树

1. 什么是CART决策树：

• Cart模型是一种决策树的模型，它即可以用于分类，也可以用于回归
• Cart回归树使用平方误差最小化策略
• Cart分类生成树采用的基尼指数最小化策略

2. 基尼值（Gini）：从数据集D中随机抽取两个样本，其类别标记不一致的概率

• 计算公式：$Gini(D)={\sum }_{k=1}^{|y|}{\sum }_{k\ne k}{p}_k{p}_k=1-{\sum }_{k=1}^{|y|}{p}_k^2$
• 基尼值越小，代表数据集D的纯度越高

3. 基尼指数（Gini_index）：选择使划分后基尼系数最小的属性作为最优化分属性

• 计算公式：$Gin{i}_{-}index(D,a)={\sum }_{v=1}^V\frac{D^v}{D}Gini(D^v)$
• 信息增益（ID3）、信息增益率（C4.5）越大，则说明优先选择该特征；但基尼指数（cart）越小，则说明优先选择该特征

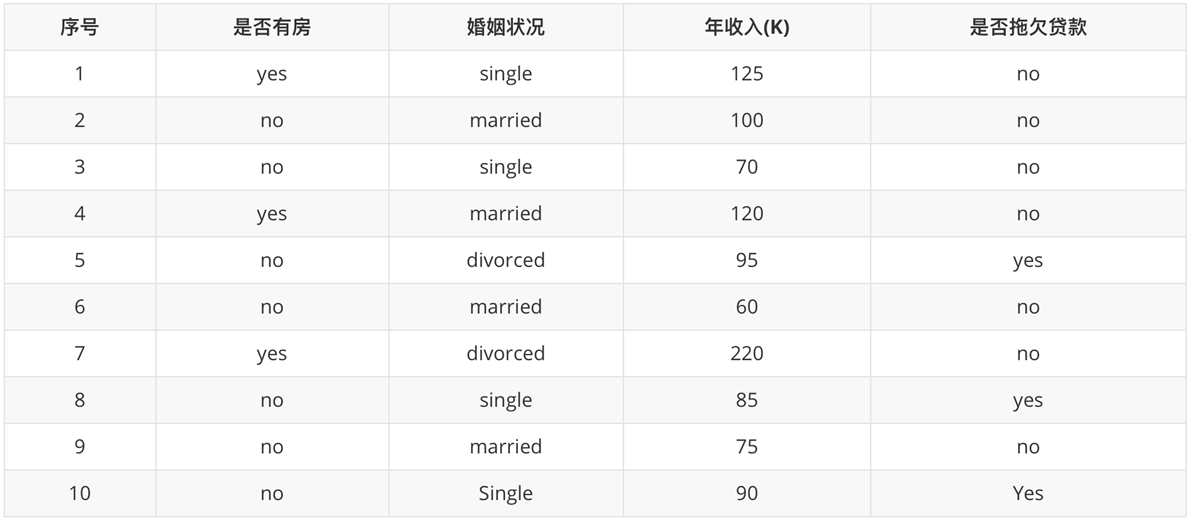
现在希望计算各特征的基尼指数，选择最优分裂点

• 是否有房：

  • 有房子的基尼值：有房子有1、4、7共计三个样本，对应：3个no、0个yes
  • $Gini(\text{是否有房,yes })=1-{\left(\frac{0}{3}\right)}^2-{\left(\frac{3}{3}\right)}^2=0$
  • 无房子的基尼值:无房子有2、3、5、6、8、9、10共七个样本，对应：4个no、3个yes
  • $Gini(\text{是否有房,no})=1-{\left(\frac{3}{7}\right)}^2-{\left(\frac{4}{7}\right)}^2=0.4898$
  • 基尼系数：第一部分样本占了总样本的3/10、第二部分样本占了总样本的7/10
  • ${\mathrm{Gini}}_{-}index(D,\text{ 是否有房 })=\frac{7}{10}\ast 0.4898+\frac{3}{10}\ast 0=0.343$

• 婚姻情况（由于婚姻情况有三个值，我们需要将其变为两个值）：

  • 1、计算{married}和{single,divorced}情况下的基尼指数
    • 结婚的基尼值，有2、4、6、9共4个样本，并且对应目标值全部为no:
    • $\mathrm{Gini}(D,\text{ married })=0$
    • 不结婚的基尼值，有1、3、5、7、8、10共6个样本，并且对应3个no，3个yes：
    • $\mathrm{Gini}(D,\mathrm{singfe},\mathrm{divorced})=1-{\left(\frac{3}{6}\right)}^2-{\left(\frac{3}{6}\right)}^2=0.5$
    • 以 married 作为分裂点的基尼指数:
    • $\mathrm{Gini}\mathrm{index}(D,\mathrm{married})=\frac{4}{10}\ast 0+\frac{6}{10}\ast 0.5=0.3$
  • 2、计算{single}|{married,divorced}情况下基尼指数
  • $\mathrm{Gin}{\mathrm{i}}_{\mathrm{i}}\mathrm{ndex}(D,\text{ 婚姻状况 })=\frac{4}{10}\ast 0.5+\frac{6}{10}\ast \left[1-{\left(\frac{1}{6}\right)}^2-{\left(\frac{5}{6}\right)}^2\right]=0.367$
  • 3、计算{divorced}|{single,married}情况下基尼指数
  • $\mathrm{Gin}{\mathrm{i}}_{-}\mathrm{index}(D,\text{婚姻状况 })=\frac{2}{10}\ast 0.5+\frac{8}{10}\ast \left[1-{\left(\frac{2}{8}\right)}^2-{\left(\frac{6}{8}\right)}^2\right]=0.4$
  • 结论：{married}和{single,divorced}情况下的基尼指数为0.3最小，选择其为分裂点

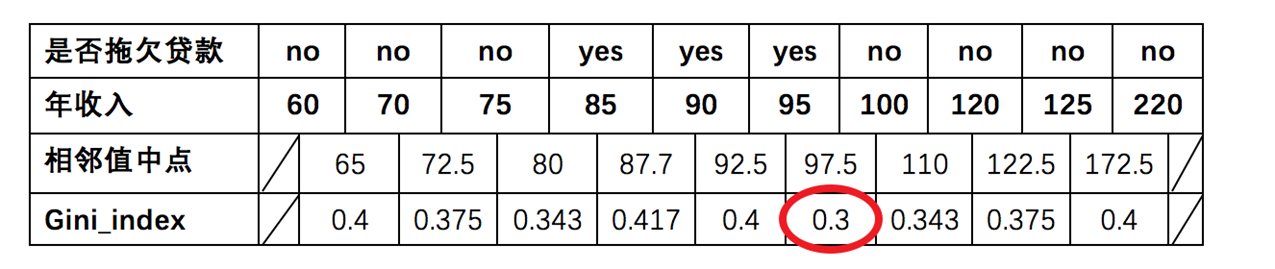
• 年收入（为连续值）：

  • 由于为连续值，因此需要取两点之间的平均值作为待分裂点：65、72.5、80、87.7、92.5、97.5、110、122.5、172.5
  • 以年收入为65将样本分为小于65和大于65两部分，计算基尼指数：
  • 节点为 65 时:{ 年收入 }=110∗0−910∗[1−(69)2−(39)2]=0.4\text{节点为 65 时}:\{\text{ 年收入 }\}=\frac{1}{10}*0-\frac{9}{10}*\left[1-\left(\frac{6}{9}\right)^2-\left(\frac{3}{9}\right)^2\right]=0.4节点为 65 时:{ 年收入 }=101​∗0−109​∗[1−(96​)2−(93​)2]=0.4
  • 以此类推计算所有分割点的基尼指数，最小为0.3

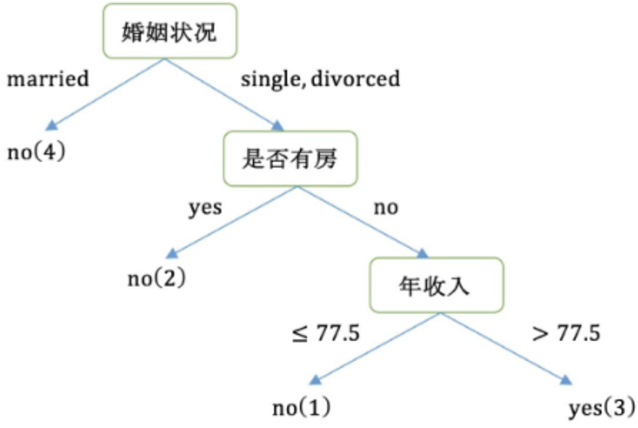
• 第一轮结果：

  • 以是否有房作为分裂点的基尼指数：0.343
  • 以婚姻状况为分裂特征、以married作为分裂点的基尼指数：0.3
  • 以年收入作为分裂特征，以97.5作为分裂点的基尼指数：0.3

• 第二轮：

  • 样本2、4、6、9样本的类别都是no，已经达到最大纯度所以，该节点不需要再继续分裂
  • 样本1、3、5、7、8、10样本中仍然包含4个no，2个yes该节点并未达到要求的纯度,需要继续划分
  • 右子树的数据集变为：1、3、5、7、8、10，在该数据集中计算不同特征的基尼指数，选择基尼指数最小的特征继续分裂

五、三种分类树对比

名称	分支方式	特点
ID3	信息增益	1.ID3只能对离散属性的数据集构成决策树 2.倾向于选择取值较多的属性
C4.5	信息增益率	1.缓解了ID3分支过程中总喜欢偏向选择值较多的属性 2.可处理连续数值型属性,也增加了对缺失值的处理方法 3.只适合于能够驻留于内存的数据集,大数据集无能为力
CART	基尼指数	1.可以进行分类和回归,可处理离散属性,也可以处理连续属性 2.采用基尼指数,计算量减小 3.一定是二叉树

六、CART回归决策树

1. CART回归树和CART分类树的区别：

• CART分类树预测输出的是一个离散值，CART回归树预测输出的是一个连续值
• CART分类树使用基尼指数作为划分、构建树的依据，CART回归树使用平方损失
• 分类树使用叶子结点多数类别作为预测类别，回归树采用叶子节点里均匀值作为预测输出

2. CART回归树的平方损失：$\mathrm{Loss}(y,f(x))=(f(x)-y{)}^2$

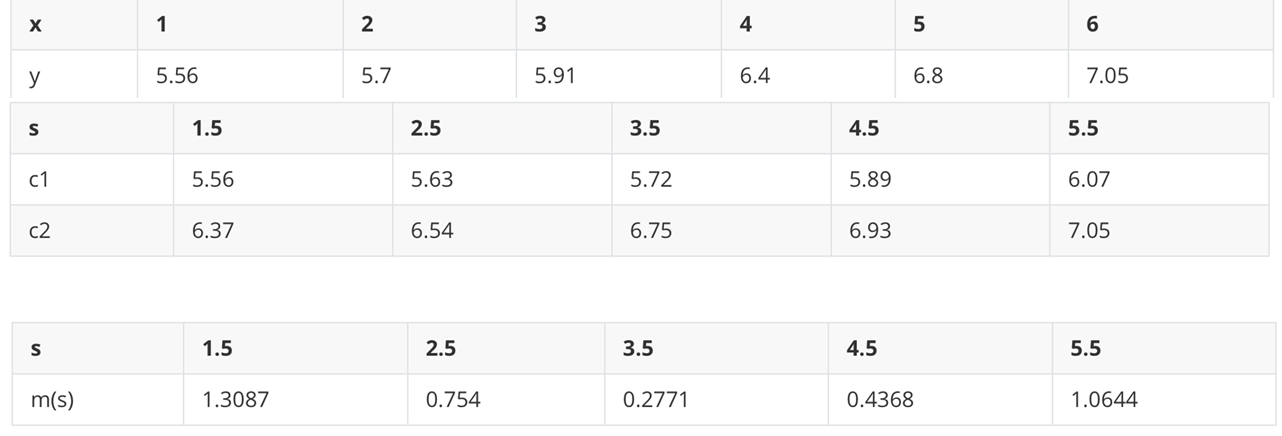
已知数据集只有1个特征x，目标值为y，现需根据平方损失，构建CART回归树

• 先划分待分裂点

• 计算划分点1.5的平方损失:

  • R1为小于1.5的样本个数，数量为1，输出值为：$R1=5.56$
  • R2为大于1.5的样本个数，数量为9：$R2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.50$
  • 计算该划分点的平方损失：$$L(1.5)=(5.56-5.56{)}^2+\left[(5.7-7.5{)}^2+(5.91-7.5{)}^2+\dots +(9.05-7.5{)}^2\right]=0+15.72=15.72$$

• 以此类推计算2.5、3.5的划分点的平方损失：

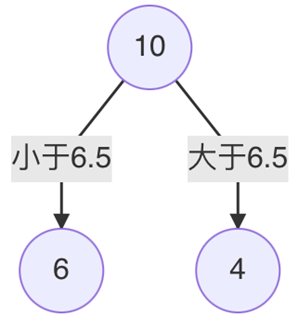
• 当划分点s=6,5时，m（s）最小，所以第一个切分点为6.5
  
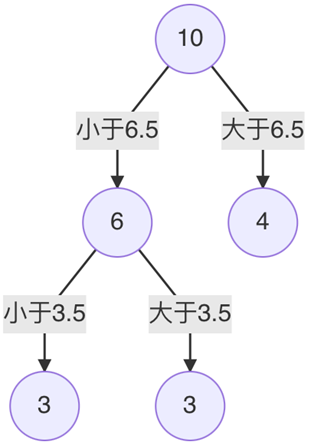
  这里是引用

• 对左子树的6个节点计算每个划分点的平方损失，找出最优划分点 在这里插入图片描述

• 因此当s=3.5时，m（s）最小，所以左子树继续以3.5进行分裂
  

• 以此类推

4. 案例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
# 创建数组
x = np.array(range(1,11)).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
# 实例化模型
estimator1 = DecisionTreeRegressor(max_depth=3)
estimator2 = DecisionTreeRegressor(max_depth=5)
estimator3 = LinearRegression()
# 模型数量
estimator1.fit(x,y)
estimator2.fit(x,y)
estimator3.fit(x,y)
# 模型预测
x_test = np.arange(0.0, 10.0, 0.01).reshape(-1, 1)
y_pre1 = estimator1.predict(x_test)
y_pre2 = estimator2.predict(x_test)
y_pre3 = estimator3.predict(x_test)
# 图像
plt.figure(figsize=(16,8))
plt.plot(x_test,y_pre1,'r-',label='max_depth=3')
plt.plot(x_test,y_pre2,'b-',label='max_depth=5')
plt.plot(x_test,y_pre3,'y-',label='liner')
plt.legend(loc='best')
plt.show()

发现深度为5的CART决策树过拟合，而线性回归泛化性更好

七、决策树剪枝

1. 剪枝是指将一颗子树的子节点全部删掉，利用叶子节点替换子树(实质上是后剪枝技术)，也可以（假定当前对以root为根的子树进行剪枝）只保留根节点本身而删除所有的叶子，以下图为例：
   

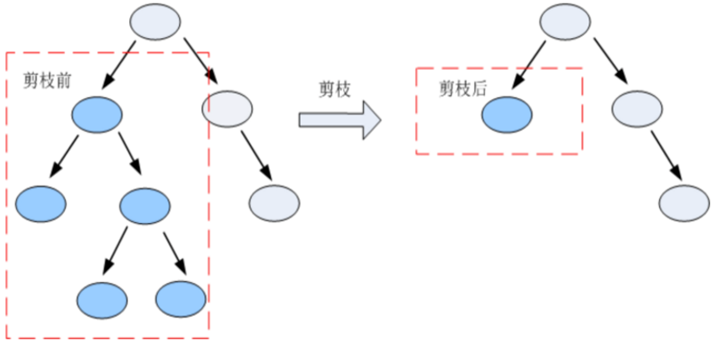
7.1 剪枝方法

1. 预剪枝：指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点
   

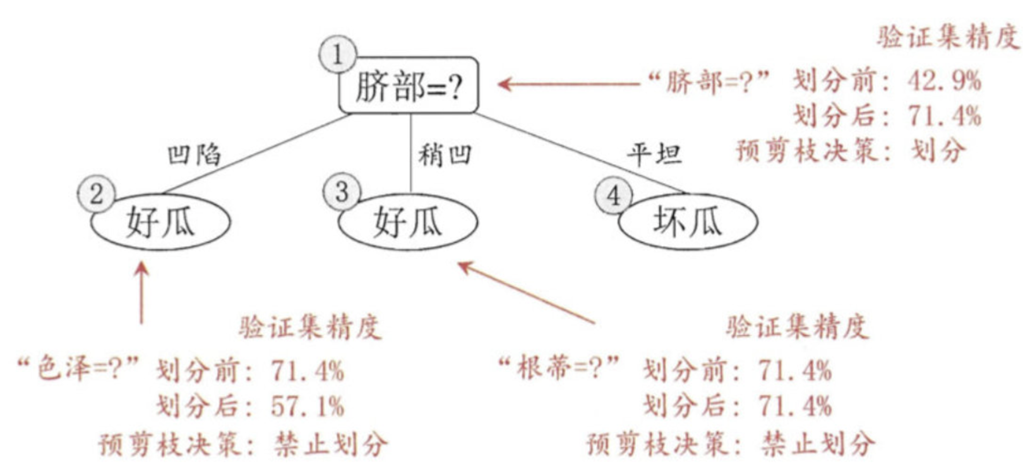
2. 后剪枝：先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点
   

7.2 对比

	预剪枝	后剪枝
优点	预剪枝使决策树的很多分支没有展开，不单降低了过拟合风险，还显著减少了决策树的训练、测试时间开销	比预剪枝保留的更多的分支，一般情况下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝
缺点	有些分支的当前划分虽不能提上泛化性能，但后续划分却有可能显著提高性能，预剪枝决策树也带来了欠拟合的风险	后剪枝先生成树，训练时间开销比未剪枝的决策树和预剪枝的决策树都要大很多