基础组合计数（三道例题）

整理了三个难度适中的组合数学题目，码蹄杯省赛和国赛的题目以及以及一道div2D难度依次递增。

组合数模板代码

#define ll long long
const ll N = 200010, mod = 998244353;
ll fac[N], invf[N];ll qmi(ll a, ll b ){ll res = 1;a %= mod;while(b){if(b & 1)res = res * a % mod;b >>= 1;a = a * a % mod;}return res;
}ll inv(ll x){return qmi(x, mod - 2);
}void init(){fac[0] = 1;for (ll i = 1; i < N; i ++)fac[i] = fac[i - 1] * i % mod;for (ll i = 0; i < N; i ++){invf[i] = inv(fac[i]);}
}ll C(ll m  ,ll n ){if( n < 0 || m < 0 || m < n )return 0;return fac[m] * invf[m - n] % mod * invf[n] % mod;
}

8、誊改文书

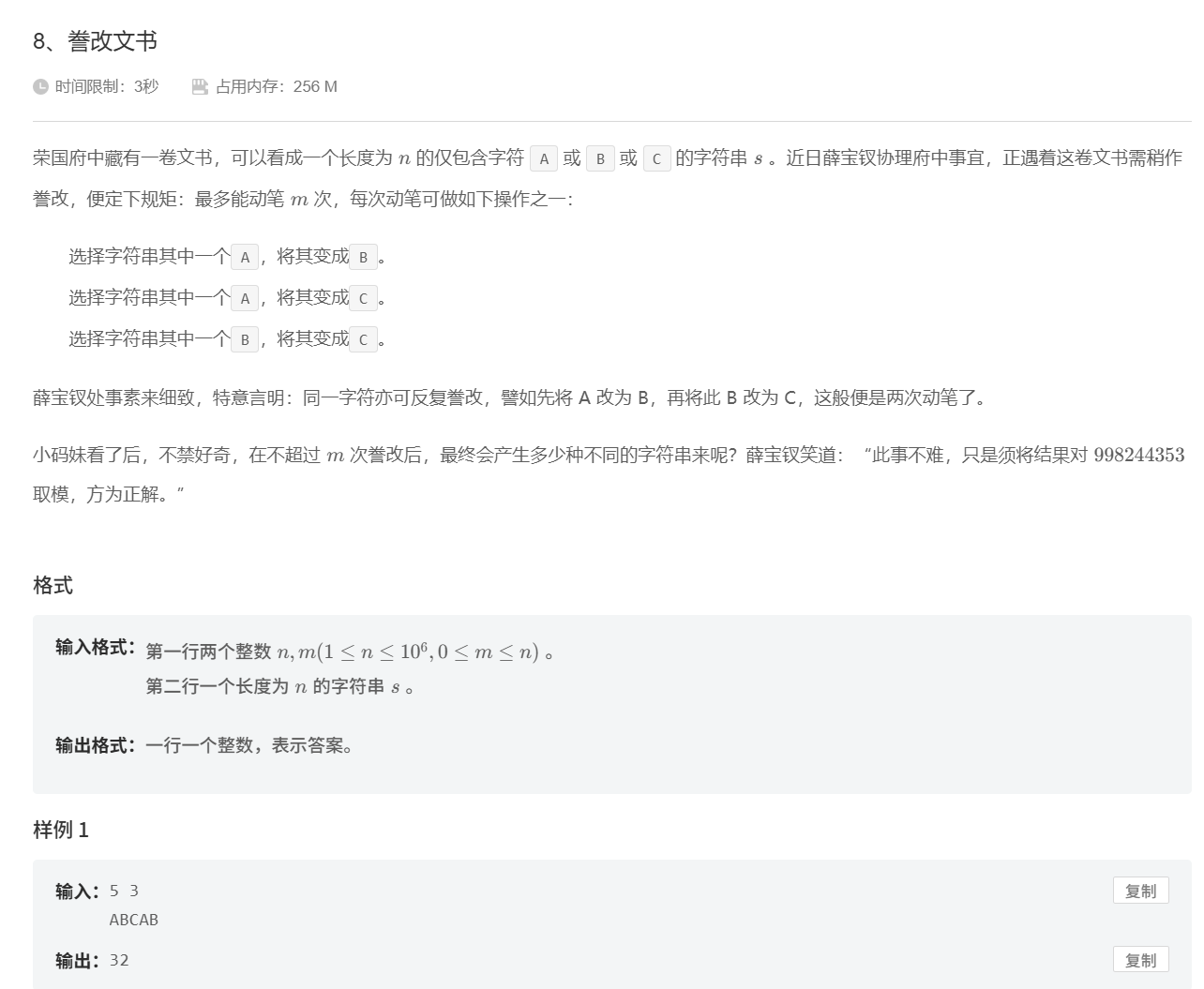
分析：码蹄杯国赛题目质量还是挺高的，通过读题我们发现只有三种操作A->B A->C B->C ，A->B->C是可以忽略掉的，因为明明少一次操作就可以完成，为什么要多一次呢，然后我们枚举对A的操作数，再对B进行前缀和的操作就可以了。

详细思路如下：

• 问题转化: 将问题从“模拟操作”转化为一个组合计数问题。最终的字符串由 “哪些'A'被改了”、“它们变成了什么”以及“哪些'B'被改了”这三个因素唯一确定。

• 核心枚举: 代码的核心思想是枚举要修改的 'A' 的数量，我们设这个数量为 x。x 的取值范围是从 0 到 min(总'A'数, 总操作数m)。

• 分步计算 (乘法原理): 对于每一个确定的 x，分两步计算方案数：

  • 第一步 (处理 'A'):

    • 计算从所有'A'中选出 x 个的方案数：C(总’A’数,x)。

    • 这 x 个'A'，每个都有'B'或'C'两种变化，总变化方案数：2x。

  • 第二步 (处理 'B'):

    • 修改'A'用掉了 x 次操作，还剩下 m-x 次。

    • 用这 m-x 次操作去修改'B'。我们可以选择修改 0 个'B'、1 个'B'、...、最多 min(m−x,总’B’数) 个'B'。这部分的总方案数是 ∑C(总’B’数,i)。

• 预处理与优化: 直接在循环中计算第二步的组合数之和效率很低。因此，代码通过预处理计算出组合数的前缀和 (pre数组)，使得在循环内只需 O(1) 的时间就能查询到结果，从而优化了整体算法的效率。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
// 对于一个组合数需要计算的就是 C(m , n )
// 就是 m 的 阶乘  乘 n的阶乘的逆元 乘 m - n 的阶乘的逆元
const int N = 1e6 + 10 , mod = 998244353;
ll fac[N] , pre[N] , invf[N];ll qmi( ll a , ll  b){a = a % mod;ll res = 1 ;while(b){if(b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}ll inv(ll x){return qmi(x , mod - 2 );
}void init(){fac[0] = 1;for(int i = 1; i < N ; i ++){fac[i] = fac[i-1] * i % mod;}for(int i = 0 ; i < N ; i ++){invf[i] = inv(fac[i]);  //求出阶乘的逆元}
}ll C(int m ,int n){return fac[m] * invf[n] % mod  * invf[m-n] % mod;
}void prem(int b){pre[0] = 1;for(int i = 1 ; i <= b ; i ++){pre[i] = (pre[i-1] + C(b , i)) % mod;}
}void solve(){int n , m ;string s;cin >> n >> m ;cin >> s;int suma = 0 , sumb = 0 ;for(int i =0  ;  i< n ;i ++){if( s[i] == 'A') suma ++ ;else if( s[i] == 'B') sumb ++ ;}prem(sumb);ll ans = 0 ;//预处理阶乘for(int x = 0 ; x  <= min(suma , m) ; x ++){int mx = min(m - x , sumb);ans = (ans + qmi(2 , x) * C(suma , x) % mod * pre[mx] % mod) % mod;}cout << ans << endl;
}   int main(){init();ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);solve();return 0;
}

MC0476 营救子龙

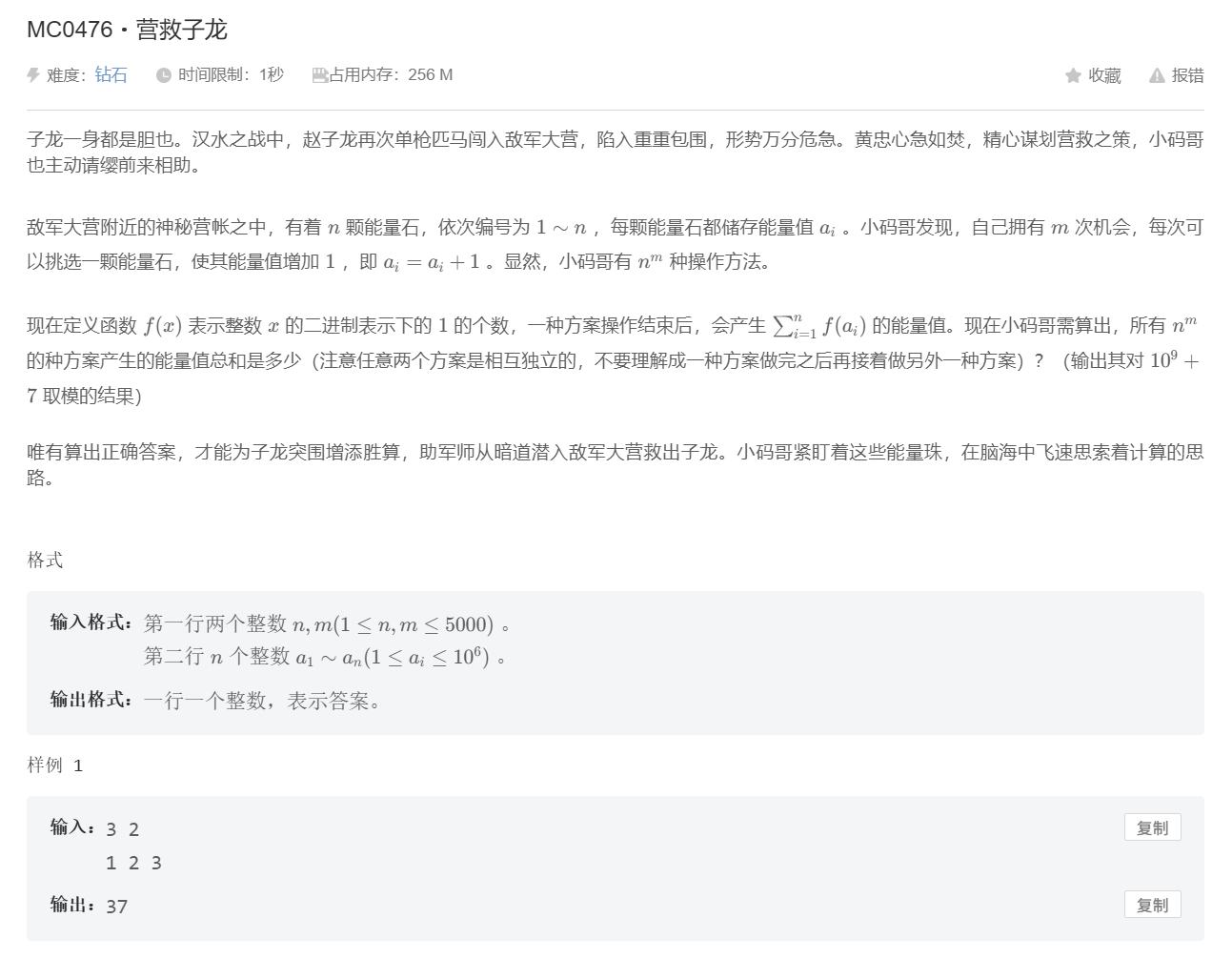
• 核心思想：贡献法 由于总方案数 nm 巨大，无法直接枚举。因此转换思路，不再计算“每种方案的能量和”，而是反过来计算“每个能量石在所有方案中贡献的能量总和”，最后将所有能量石的贡献相加。

• 计算单体贡献 对单个能量石 i，我们枚举它在 m 次操作中被增加了 j 次（j 的范围是 0 到 m）。

  • 能量值: 当它被增加 j 次时，其能量值为 f(ai​+j)。

  • 方案数: 利用组合数学计算这种情况出现了多少次。在 m 次操作中选 j 次给它，有 Cmj​ 种选法；剩下 m-j 次操作分配给其它 n-1 个石头，有 种方法。总方案数即为

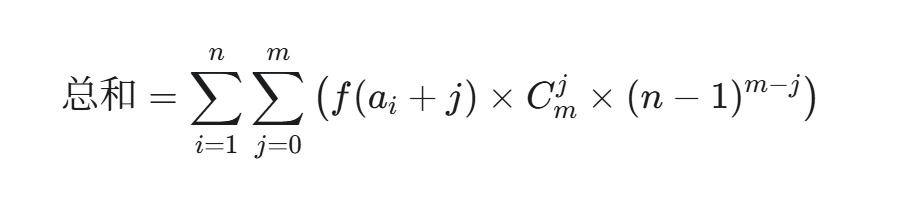
#include<bits/stdc++.h>
using namespace std;
typedef long long ll ;
#define endl "\n"
const int N = 5010 , mod = 1e9 + 7;
ll a[N]; 	// 对前i个数字 j次 得到的值
ll b[N][N] ,qm[N]; // 记录 i个数字操作 了 j次有几个 1
ll c[N];
int cl(ll x){int cnt = 0 ;while(x){if(x&1) cnt ++ ;x/=2;}return cnt;
}
ll qmi(ll a, ll b){ll res = 1;while(b){if(b & 1) res = res * a % mod;a = a *a % mod;b >>= 1;}return res;
}
void solve(){int n , m ;cin >>n >>m ;for(int i = 0 ; i<n ; i ++)cin >>a[i];c[0] = 1;for(int j = 1 ; j <= m ; j ++){c[j] = c[j- 1] *( m - j + 1) %mod  * qmi( j , mod - 2) %mod ;                                }for(int i = 0 ; i <= m; i++){qm[i] = qmi(n -1 , i);}for(int i = 0 ; i < n ; i++){b[i][0] = cl(a[i]);for(int j = 1 ; j <= m; j ++){a[i] ++;b[i][j] = cl(a[i]);}}ll ans = 0 ;for(int i = 0 ; i < n ;i ++){for(int j = 0 ; j <=m ; j ++){ans = (ans + b[i][j] * c[j] % mod * qm[ m - j ] % mod) % mod;}}cout <<ans << endl;return ;
}signed main(){ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);	solve();return 0 ;
}

D. Grid Counting

分析：读题多举例子可以发现需要满足的是每列有且只有一个，且第一行全能放，第二行左右第一个格子不能放，第三行左右前两个格子不能放以此类推，且需要满足放的格子数量等于n。计算组合数，这里有一个非常巧妙的技巧技巧就是从下到上依次增加我们能放的列，且放当前的列，这样最后放完之后一定是每列都放过了的。

将复杂的二维网格约束问题，转化为了一个一维的、逐层解锁可用槽位并进行组合选择的计数问题，极大地简化了求解过程。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long
const ll N = 200010, mod = 998244353;
ll fac[N], invf[N];ll qmi(ll a, ll b ){ll res = 1;a %= mod;while(b){if(b & 1)res = res * a % mod;b >>= 1;a = a * a % mod;}return res;
}ll inv(ll x){return qmi(x, mod - 2);
}void init(){fac[0] = 1;for (ll i = 1; i < N; i ++)fac[i] = fac[i - 1] * i % mod;for (ll i = 0; i < N; i ++){invf[i] = inv(fac[i]);}
}ll C(ll m  ,ll n ){if( n < 0 || m < 0 || m < n )return 0;return fac[m] * invf[m - n] % mod * invf[n] % mod;
}void solve(){ll n ;cin >> n;vector<ll>a(n + 1);for(ll i = 1; i <= n ; i ++ )cin >> a[i];ll x = 0;ll ans = 1; for(ll i = n ;  i > 0 ; i --){if( (n & 1) && i == (n + 1 ) / 2)x += 1;if( i <= n / 2)x += 2;ans = ans * C(x, a[i]) % mod , x-= a[i];}if(x == 0 )cout << ans << endl;elsecout << 0 << endl;
}int main(){ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);init();ll t;cin >>t;while(t--) solve();return 0;
}