算法专题（三）01背包问题理论

零、动规五部曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

题目：

一、dp的含义

dp[i][j]表示第0个到第i-1个的物品中放入容量为j的背包中的最大价值

二、确定递推公式

分为两个部分：不放物品i和放物品i

1、不放物品i

dp[i][j]=dp[i-1][j]

就是说容量没变化（从dp[i-1][j-1]到dp[i-1][j]），但是只放入了0到i-1中的物品，最后赋值给dp[i][j]

2、放物品i

dp[i][j]=dp[i-1][j-weight[i]]+value[i]

就是说硬塞进物品i，容量得减去第i个物品的重量，剩下的也是0到i-1中的物品，然后再加上i的价值，最后赋值给dp[i][j]

3、最终递推公式：

dp[i][j]=Max（dp[i-1][j]，dp[i][j]=dp[i-1][j-weight[i]]+value[i]）

三、dp数组如何初始化

因为是二维数组，我们从递推公式也可以看出，[i][j]只和[i][j-1]、[i-1][j-weight[i]]有关，意思就是数据只会从左上来，所以我们只考虑第一行和第一列

数组：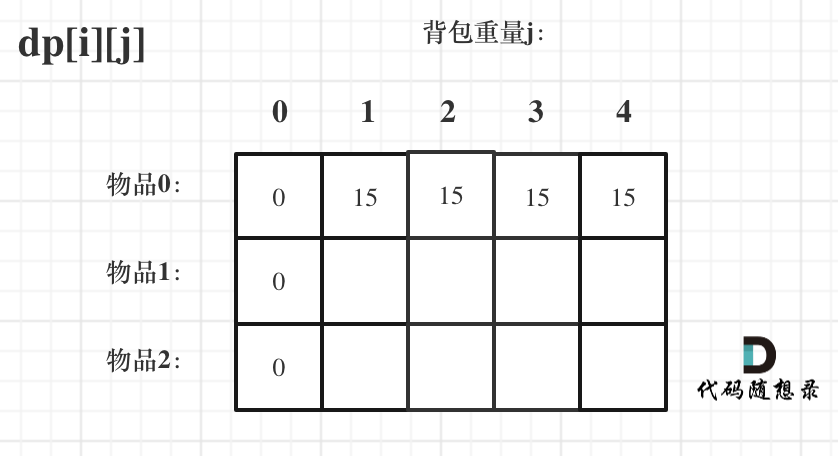

第一列背包重量为j=0，所以价值都是0

第一行从能放入物品0开始都是物品0的重量

因此初始化完成

四、确定遍历顺序

        for (int i = 1; i < n; i++) {for (int j = 0; j <= bagweight; j++) {if (j < weight[i]) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}}

这道题因为只和左上有关系，所以先背包还是先物品都可以

五、举例推导dp数组

自行推导

资源来源：代码随想录