【杀鸡焉用牛刀？】基于模板匹配的极简OCR实现

@[toc]
1.引言
2.什么是OCR？
3.图像预处理与字符分割
4.模板匹配算法
5.后处理与识别矫正
6.*对数据的理解

引言

本文的写作动机是近代物理实验课程中因为没有更智能的设备所以要求实验者拍摄某个显示屏并进行OCR以提取我们需要的数据，并进行曲线绘制。

OCR，即Optical Character Recognition，光学字符识别。似乎这已经是一件司空见惯、随手就能够做的事情，网上肯定有大把大把现成的开源库。但是事实上，笔者尝试了诸如$\text{paddleocr}$ , $\text{Tesseract-OCR}$等等一众知名开源OCR库后，却惊讶地发现他们都做不好这样一个问题。

按照一般的解决，如果我们使用传统方法解决不了问题，那么就势必上深度学习了。于是下一步就应该是打开Github，仔细检索是否有做相关字体的OCR的预训练完成的深度学习模型…

但是，真的有必要吗？如果的确那么做了，除了是更熟练地会点击download之外1，似乎没有别的益处了。况且，图片中的数字很清晰，也不存在较大幅度的位移，一定能够有更简单的办法完成。

经过一小会儿时间的思考与检索之后，最终敲定了模板匹配这样一个方法。在正式介绍方法之前，不妨先让我们对OCR有一个最基本的了解：

如果读者嫌弃CSDN的奇怪排版，可以移步公众号：【杀鸡焉用牛刀？】基于模板匹配的极简OCR实现

什么是OCR？

OCR，全称为光学字符识别（Optical Character Recognition），是一种通过图像处理和模式识别技术，将图像中的印刷或手写文字转换为可编辑、可搜索的数字文本的过程。它本质上涉及从像素级别的视觉数据中提取语义信息，通常包括：

1. 图像预处理（如二值化、去噪和校正倾斜）

2. 字符分割、特征提取（如边缘检测或统计特征）

3. 最终分类识别步骤。

4. 后处理与识别矫正

这项技术的发展可追溯到20世纪50年代初，当时的系统主要针对特定字体，如银行支票上的磁性墨水字符（MICR），采用光学扫描结合模板匹配的方法，准确率依赖于图像质量和字体标准化。随着数字计算能力的提升，70年代引入了更先进的特征提取技术，如傅里叶描述子，而80年代的统计模式识别进一步提高了鲁棒性。进入21世纪，机器学习尤其是深度神经网络（如卷积神经网络CNN和循环神经网络RNN）的应用，使得OCR能够处理多语言、变体字体乃至自然场景下的文本，例如倾斜、模糊或背景复杂的图像，如街头标志或历史文献扫描件。

然而，在特定应用中，如我们实验中显示屏上的固定数字字体，现成OCR库的泛化能力有时不足以应对高度结构化的简单场景。这也突显了OCR的科学基础：它不仅是工程工具，更是计算机视觉与人工智能的交叉领域，强调从图像中推断结构化信息的算法效率，而非一味依赖复杂模型。

我们不妨简单地介绍一下对于目前笔者遇到的任务，笔者进行OCR处理的思路：

1. 在视频中按一定的间隔切取图片：

2. 对图片进行预处理并进行分割出目标区域，再将目标区域等分为五部分：

我们需要的是字符与字符相匹配，所以要切出字符

3. 最终的分类识别步骤：
   • 我们首先将一部分图像存做模板。因为我们的识别结果只可能为十二种:$\text{0123456789-E}$
   • 对于输入的视频，进行预处理和切分之后，对于每个位置的数字，我们计算其与模板之间的向量相似度。大家不妨简单地理解为，我们可以将图片展平为一个一维的向量，计算两个向量之间的$\cos \theta$即可得到相似度。

图像预处理与字符分割

首先，我们简要介绍一下计算机如何存储图片的基本知识：数字图像本质上是一个二维（或三维，包括颜色通道）像素阵列，每个像素由整数值表示亮度或颜色。通常，灰度图像每个像素用8位（0-255）表示黑白强度，而彩色图像（如RGB）则有三个通道，每个通道独立存储红、绿、蓝分量。图像存储为位图（raster），像素按行和列排列，形成矩阵结构。在处理中，我们常使用OpenCV等库操作这些矩阵，实现变换、滤波和分割。

针对本实验中显示屏数字的OCR任务，我们采用以下预处理流程，以优化图像质量并隔离感兴趣区域。并且好消息是，下面的几个步骤在$\text{OpenCV}$库中都有现成的实现。

1. 转换为灰度图：原始帧通常是彩色（BGR格式，在OpenCV中），但颜色信息对数字识别往往冗余且可能引入噪声。将图像转换为灰度（单通道）简化了数据，聚焦于亮度差异，便于后续阈值化和边缘检测。这减少了计算复杂度，同时保留了字符的结构信息。

2. 应用高斯模糊以减少噪声：高斯模糊是一种低通滤波器，使用高斯核（如(3,3)大小）对图像进行卷积，平滑像素值以抑制随机噪声（如相机抖动或光照不均引起的颗粒）。这有助于防止噪声被误识别为字符边缘，同时保持整体轮廓完整，避免过度模糊导致细节丢失。

   高斯模糊的核心是用高斯核 $G(x,y)$ 对图像 $I(x,y)$ 做卷积：

   $$I^{\prime }(x,y)=\sum _{u=-k}^k\sum _{v=-k}^{k}I(x+u,y+v)G(u,v)$$

   其中，高斯核定义为：

   $$G(x,y)=\frac{1}{2\pi {\sigma }^2}\exp (-\frac{x^2+y^2}{2{\sigma }^2})$$

3. 应用自适应阈值处理：自适应阈值（如Gaussian C方法）将灰度图像二值化为黑白（0或255），根据局部像素统计动态计算阈值（块大小11，常数2）。相比全局阈值，这更适合光照不均匀的场景，能更好地分离前景（数字）和背景，提高字符的清晰度。

   在自适应阈值中，每个像素点 $(x,y)$ 的二值化结果取决于其邻域均值（或高斯加权均值）：

   $$I’(x,y) =
   \begin{cases}
   1, & I(x,y) > \frac{1}{|N|}\sum_{(u,v)\in N(x,y)} I(u,v) - C $KaTeX parse error: Expected 'EOF', got '&' at position 10: 6pt] 0, &̲ \text{otherwis…$

   其中，$N(x,y)$ 表示邻域窗口，$C$ 为常数修正项。

4. 使用形态学操作进行“去噪”和“填充”：形态学操作基于结构元素（这里是3x3矩形核）。开运算（MORPH_OPEN）先腐蚀后膨胀，用于去除小噪声点和孤立像素；闭运算（MORPH_CLOSE）先膨胀后腐蚀，用于填充字符内部的小孔或连接断开的笔画。这两个操作结合，能平滑字符边界，增强连通性，提高后续分割的鲁棒性。

   形态学操作基于集合运算，常见定义如下：

   • 腐蚀（erode）：
     $$(A\ominus B)(x)=\underset{b\in B}{\min }A(x+b)$$

   • 膨胀（dilate）：
     $$(A\oplus B)(x)=\underset{b\in B}{\max }A(x-b)$$

   • 开运算（open）：
     $$A\circ B=(A\ominus B)\oplus B$$

   • 闭运算（close）：
     $$A\bullet B=(A\oplus B)\ominus B$$

   这里 $A$ 是图像，$B$ 是结构元素（如 $3\times 3$ 矩形核）

5. 图像反转（如果必要）：通过检查中心区域的平均亮度（>127表示偏亮），决定是否 bitwise_not 反转图像。这适应不同显示屏的颜色方案（如黑底白字或白底黑字），确保前景（数字）始终为白色、背景为黑色，便于统一处理和模板匹配。

预处理后，我们进一步裁剪数字区域（使用预定义ROI参数，如CROP_ROI_X等），避免无关部分干扰OCR。这一步通过边界检查确保有效性，若ROI无效则回退到整图。裁剪后图像即为OCR输入，准备进行字符分割：假设数字固定为五位，我们等分区域（如前文所述），每个子区域对应一个字符，便于独立匹配模板。

这些步骤构成了一个典型的OCR预处理管道，强调从原始像素数据中逐步提取结构化特征，最终为模板匹配铺平道路。在实际实现中，可根据具体图像特性微调参数，以最大化准确率。

模板匹配算法

大家不妨简单地理解为，我们可以将图片展平为一个一维的向量，计算两个向量之间的$\cos \theta$即可得到相似度。

虽然在上文中告诉了大家“简单理解”，但如果实际计算中这么操作，效果肯定不会很好（毕竟太过于粗糙了）。这种时候，几乎可以肯定的是，一定存在更合理的算法，只是看我们选择什么：

OpenCV 提供了多种模板匹配方式，主要区别在于相似度的计算公式。

在以下公式中：

• $I(x,y)$ 表示原始图像的像素值
• $T(x,y)$ 表示模板图像的像素值
• $(x,y)$ 是模板在原图中的左上角位置
• $\bar{T}$ 表示模板像素的均值
• ${\bar{I}}_{x,y}$ 表示图像在窗口 $(x,y)$ 内的均值

---

1. 平方差匹配（Squared Difference）

• 方法：cv2.TM_SQDIFF
• 归一化版本：cv2.TM_SQDIFF_NORMED
• 公式：
  $$R(x,y)=\sum _{x^{\prime },y^{\prime }}(T(x^{\prime },y^{\prime })-I(x+x^{\prime },y+y^{\prime }){)}^2$$
  值越小表示匹配度越高。

---

2. 相关匹配（Cross Correlation）

• 方法：cv2.TM_CCORR
• 归一化版本：cv2.TM_CCORR_NORMED
• 公式：
  $$R(x,y)=\sum _{x^{\prime },y^{\prime }}(T(x^{\prime },y^{\prime })\cdot I(x+x^{\prime },y+y^{\prime }))$$
  归一化形式：
  $$R_{norm}(x,y)=\frac{{\sum }_{x^{\prime },y^{\prime }}T(x^{\prime },y^{\prime })\cdot I(x+x^{\prime },y+y^{\prime })}{\sqrt{{\sum }_{x^{\prime },y^{\prime }}T(x^{\prime },y^{\prime }{)}^2\cdot {\sum }_{x^{\prime },y^{\prime }}I(x+x^{\prime },y+y^{\prime }{)}^2}}$$
  值越大表示匹配度越高。

---

3. 相关系数匹配（Correlation Coefficient）

• 方法：cv2.TM_CCOEFF
• 归一化版本：cv2.TM_CCOEFF_NORMED
• 公式：
  $$R(x,y)=\sum _{x^{\prime },y^{\prime }}(T(x^{\prime },y^{\prime })-\bar{T})\cdot (I(x+x^{\prime },y+y^{\prime })-{\bar{I}}_{x,y})$$
  其中：
• $\bar{T}$ = 模板均值
• ${\bar{I}}_{x,y}$ = 图像在窗口 $(x,y)$ 内的均值

归一化形式：
$$R_{norm}(x,y)=\frac{{\sum }_{x^{\prime },y^{\prime }}(T(x^{\prime },y^{\prime })-\bar{T})\cdot (I(x+x^{\prime },y+y^{\prime })-{\bar{I}}_{x,y})}{\sqrt{{\sum }_{x^{\prime },y^{\prime }}(T(x^{\prime },y^{\prime })-\bar{T}{)}^2\cdot {\sum }_{x^{\prime },y^{\prime }}(I(x+x^{\prime },y+y^{\prime })-{\bar{I}}_{x,y}{)}^2}}$$

归一化后结果在 $[-1,1]$ 之间，越接近 1 表示匹配越好。

后处理与识别矫正

经过上面的操作，我们显然已经得到了我们需要的数据。但是，存在一个很直接的问题：我们真的信得过吗？

比如，在我们的问题场景（气压随时间的变化中），数据一定是单调的。但是如果我们识别的数据不单调应该这么办？这就涉及到（几乎是最重要的）后处理与识别矫正。

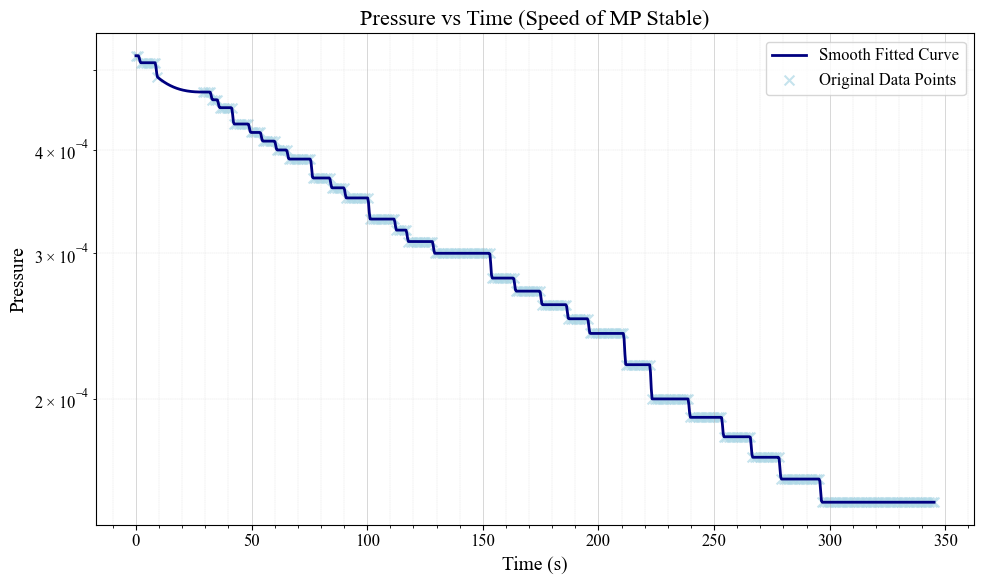
这几乎是一个专门的学问，不可能在一篇文章中说清。但是，不妨借由我们的问题，来为大家介绍两种最常用的方法（不用担心，文末的代码仓库包含了这一部分）。

首先明确，我们的任务是：保证单调性（不希望看见小幅度的忽上忽下），扣除（太离谱的）离群点。

在开始数学公式前，先统一说明文中出现的符号（只解释一次，避免重复）：

• $x$ 或 $t$：自变量（例如时间点）
• $y$ 或 $p$：观测值（例如原始或有效的压力值）
• $T_q$：第 $q$ 百分位数（例如 $T_{25}$ 为第 25 百分位）
• $\mathrm{IQR}$：四分位距，$\mathrm{IQR}=T_{75}-T_{25}$
• $k$：用于扩展 IQR 的倍数系数（例如常用 $k=1.5$ 或更保守的 $k=3$）
• $\hat{f}$：拟合得到的单调函数（或序列）
• $w_i$：权重（若未指定一般取 $1$）
• 索引 $i$、$a,b$：表示序列中的位置或区间端点

---

一、IQR 离群点检测

核心思想：用第 25 和第 75 百分位定义数据的“箱体”，把远离箱体外部的点视作离群点。公式非常直接。

1. 计算下四分位与上四分位：
   $$T_{25}=\text{percentile}(y,25),T_{75}=\text{percentile}(y,75)$$

2. 计算四分位距：
   $$\mathrm{IQR}=T_{75}-T_{25}$$

3. 计算离群点判定上下界：
   $$\text{lower\_bound}=T_{25}-k\cdot \mathrm{IQR},\text{upper\_bound}=T_{75}+k\cdot \mathrm{IQR}$$

4. 离群点掩码（布尔数组）：
   $${\text{is\_outlier}}_i=(y_i<\text{lower\_bound})\vee (y_i>\text{upper\_bound})$$

5. 过滤得到的非离群点序列：
   yfiltered={yi:¬is_outlieri}y_{\text{filtered}} = \{y_i: \neg \text{is\_outlier}_i\} yfiltered​={yi​:¬is_outlieri​}

直观说明与小提示：

• 常用 $k=1.5$（较严格）或 $k=3$（较宽松），你脚本中用 $k=3$ 更保守地只删极端值，适合含噪但不想丢太多点的场景。
• IQR 方法对偏态分布或带有季节/趋势的数据可能会误判（因为它基于分位数而非全局模型）。在你的场景中，先用 IQR 快速去极端值再拟合单调模型是一个稳妥的工程折衷。
• 如果过滤后点太少（例如少于 2 个），应回退到不滤除或降低 $k$，你脚本里已做了这种鲁棒处理，很棒。

---

二、单调回归与 PAV 算法

目标（数学形式）

你想拟合一个满足单调性约束的序列 $\hat{f}=({\hat{f}}_1,{\hat{f}}_2,\dots ,{\hat{f}}_n)$，在 L2 意义下最接近观测 $y=(y_1,\dots ,y_n)$。若期望单调递减（increasing=False），问题可以写作：

$$\hat{f}=\arg \underset{f}{\min }\sum _{i=1}^n{w}_i(y_i-f_i{)}^2\text{subject to}{f}_1\ge f_2\ge \cdots \ge f_n.$$

（若要单调递增，只需把不等号反过来。）

这里 $w_i$ 是权重（默认 $w_i=1$）。

Pool Adjacent Violators算法

PAV 算法是求解上述问题的经典线性时间近似算法（严格说是最优且常用的算法）。核心思路：

• 从左到右把每个点当作一个「块（block）」，块内值取该块的加权平均；
• 若相邻两个块违反单调性约束（比如希望递减但左块均值小于右块均值），就把这两个块合并成一个更大的块并用合并后的加权平均替代；
• 持续合并直到所有相邻块满足单调性。

若区间 $[a,b]$ 被合并为一个块，则该块的加权平均为：

$${\bar{y}}_{a:b}=\frac{{\sum }_{i=a}^b{w}_i{y}_i}{{\sum }_{i=a}^b{w}_i}$$

PAV 的最终输出就是把每个块内所有位置的 ${\hat{f}}_i$ 都设为该块的 ${\bar{y}}_{a:b}$，保证最小二乘与单调性同时成立。

算法复杂度与性质

• PAV 在一般实现下是 $O(n)$（均摊）或接近线性的，效率很高。
• 得到的 $\hat{f}$ 是观测向量 $y$ 在单调序列锥（monotone cone）上的正交投影（L2 投影），因而是全局最优解。
• 如果输入的 $x$（自变量）不是严格等间隔，Sklearn 的 IsotonicRegression 会考虑 $x$ 的顺序并在预测时对新 $x$ 做线性插值；out_of_bounds='clip' 会把预测点 $x$ 超出训练范围时的值裁剪到边界值。

sklearn 实现的一些工程细节

• 我的代码中使用的是 IsotonicRegression(increasing=False, out_of_bounds='clip')：表示你拟合单调递减函数，并在预测 $x$ 越界时使用边界值进行裁剪（不会外推）。
• fit(x, y) 时，输入 $(x_i,y_i)$ 的顺序很重要：PAV 基于 $x$ 的排序来合并相邻点。通常确保 $x$ 是递增的（或按时间排序），就像你的 t_fit。
• predict(t_all) 会对 t_all 中位于训练 $x$ 范围内的点做插值（或返回块常数值），范围外的点被裁剪到训练域的端点（当 out_of_bounds='clip'）。

---

三、工程建议（小而实用）

• 在 IQR 阶段：若数据有明显趋势（例如单调下降的压力），考虑先在局部窗口内做 IQR（分段检测），以避免把趋势性边缘点误判为离群点。
• 在 Isotonic 拟合前：确保用于拟合的点具有代表性（脚本中当过滤后点 < 2 时回退的做法非常合理）。
• 可视化：画出原始点、被判为离群点的点、拟合曲线（$\hat{f}$），这样能直观判断是否过度去除数据或拟合过度平滑。
• 如果希望保留局部波动但仍要求单调趋势，可以在拟合前对 $y$ 做小幅平滑（例如用小窗口中位数滤波），然后再做 Isotonic；或者在拟合时使用权重 $w_i$ 反映观测置信度。

---

四、示例伪代码（PAV 思路，帮助记忆）

初始化：把每个位置 i 当作一个单点块，块均值 m_i = y_i, 块权重 W_i = w_i从左到右扫描：如果当前块 m_{j} 与前一块 m_{j-1} 满足单调性（例如 m_{j-1} >= m_j 对于递减），继续否则（违反单调性）：合并前两块为新块，新的均值 = (W_{j-1}*m_{j-1} + W_j*m_j) / (W_{j-1} + W_j)新的权重 = W_{j-1} + W_j将合并后的块与更前面的块再次检查是否违反单调性（可能需要回溯合并）
结束后：每个块内的所有位置都被赋值为该块的均值，得到最终单调序列

*对数据的理解

我们采用的OCR方法十分粗糙，可以预见的是，我们一定会遇到各种各样的问题。比如笔者在运行过程中就发现，每次判别最后一位数字时，置信度就会奇低。然而还不太敢随便放宽对于最后一位置信度的审查，毕竟这设计到数量级的问题；再比如，受限于预处理、图片质量等问题，模板匹配的方法对于"-"符号的识别效果奇差

这种时候，我们的重点不应该是死磕**“我到底应该怎么提高准确度”** ，而是回到我们的数据本身，研究我们的数据特性。譬如，针对第一个问题，我们在观看视频之后，发现总是会在某一两个数量级上停留的时间较长。那么在该时间间隔内，我们就可以直接省去对于第五位的判断。

同样的道理，第三位恒定为$\text{E}$,完全也不必判定…

显然，数据本身的特性肯定不止笔者提到的几点。如果需要获取全部代码的读者可以访问Github仓库：

https://github.com/HorseRunningWild/7SD_Template_Matching_Ocr