详细案例说明AI所用的算法,列出公式,用Python代码说明用法
我们来详细拆解一个最经典、最基础的 AI 算法 ——线性回归 (Linear Regression)。它是理解几乎所有更复杂 AI 模型(如神经网络)的基石。
我会按照以下结构为你讲解:
- 核心思想与生活案例:用一个具体的例子让你明白它在做什么。
- 数学原理与所有公式:清晰地列出并解释每个公式。
- 代码实现与用法:使用 Python 和
scikit-learn库来演示如何应用。 - 算法总结:回顾线性回归的优缺点和适用场景。
1. 核心思想与生活案例
核心思想:线性回归的目标是,在一堆看似杂乱的数据点中,找到一条最佳拟合直线(或高维空间中的超平面),使得这条线到所有数据点的总误差最小。
生活案例:预测房价
假设你想根据房子的面积来预测它的价格。你收集了一些数据:
| 房子面积 (平方米) | 价格 (万元) |
|---|---|
| 50 | 100 |
| 70 | 140 |
| 80 | 165 |
| 100 | 220 |
| 120 | 260 |
如果我们把这些数据画在图上,横轴是面积 (X),纵轴是价格 (Y),会得到一些分散的点。
线性回归要做的事,就是画一条直线 y = mx + b,让这条线尽可能地 “穿过” 这些点。其中:
x是特征 (Feature),在这里是房子面积。y是目标 (Target),在这里是房子价格。m是直线的斜率 (Slope),代表面积每增加 1 平方米,价格预计会上涨多少。b是直线的截距 (Intercept),代表理论上面积为 0 时的房价(虽然在这个例子里没有实际意义)。
我们的任务就是找到最优的 m 和 b 的值。
2. 数学原理与所有公式
我们用更通用的数学符号来表示:
- 输入特征:
x_i(比如第 i 个房子的面积) - 真实输出:
y_i(比如第 i 个房子的真实价格) - 预测输出:
ŷ_i(读作 y-hat,是模型对第 i 个房子价格的预测值) - 模型参数:
w(权重 / 斜率) 和b(偏置 / 截距)
公式 1: 线性回归模型 (The Model)
这就是我们要找的那条直线的方程。

是特征向量。
公式 2: 损失函数 (Loss Function)
我们需要一个标准来衡量一条直线的 “好坏”,这个标准就是损失函数(也叫成本函数)。它计算的是所有预测值与真实值之间的总误差。
最常用的是均方误差 (Mean Squared Error, MSE)。

公式 3: 优化算法 (Optimization Algorithm)
如何找到使损失函数最小的 w 和 b最常用的方法是梯度下降 (Gradient Descent)。
核心思想:想象一下,损失函数 \(J(w, b)\) 是一座山,我们站在山上的某个位置(代表当前的 w 和 b 值)。梯度下降就像我们一步步往下走,每次都朝着坡度最陡的方向(梯度的反方向)迈一小步,直到走到山谷最低点。
更新规则 (Update Rules):
我们通过计算损失函数对每个参数的偏导数(梯度)来找到这个 “最陡的方向”,然后更新参数。

计算偏导数 (Calculating the Partial Derivatives):

这个过程会不断重复,直到损失函数的值不再显著下降,或者达到预设的迭代次数。
3. 代码实现与用法
我们使用 Python 和强大的机器学习库 scikit-learn 来实现。scikit-learn 已经封装好了所有复杂的数学计算。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression# 房子面积 (特征)
X = np.array([50, 70, 80, 100, 120]).reshape(-1, 1)
# reshape(-1, 1) 是为了把一维数组变成二维数组,因为scikit-learn的模型期望输入是2D的 (样本数, 特征数)# 房子价格 (目标)
y = np.array([100, 140, 165, 220, 260])# 1. 创建一个线性回归模型的实例
model = LinearRegression()# 2. 使用训练数据来“拟合”模型 (fit the model)
# 这个过程内部就是在执行梯度下降(或其他优化算法)来找到最优的w和b
model.fit(X, y)# 查看斜率 (w)
# coef_ 是 coefficient (系数) 的缩写
w = model.coef_[0]
print(f"模型找到的斜率 (w): {w}")# 查看截距 (b)
# intercept_ 是截距的意思
b = model.intercept_
print(f"模型找到的截距 (b): {b}")# 输出:
# 模型找到的斜率 (w): 2.075
# 模型找到的截距 (b): -3.75# 预测一个90平米的房子价格
new_area = np.array([[90]]) # 同样需要是2D数组
predicted_price = model.predict(new_area)print(f"预测一个90平米的房子价格为: {predicted_price[0]} 万元")# 预测多个房子的价格
areas_to_predict = np.array([[60], [110]])
predicted_prices = model.predict(areas_to_predict)
print(f"预测60平米和110平米的房子价格分别为: {predicted_prices} 万元")# 输出:
# 预测一个90平米的房子价格为: 183.0 万元
# 预测60平米和110平米的房子价格分别为: [120.75 224.5 ] 万元# 1. 绘制原始数据点
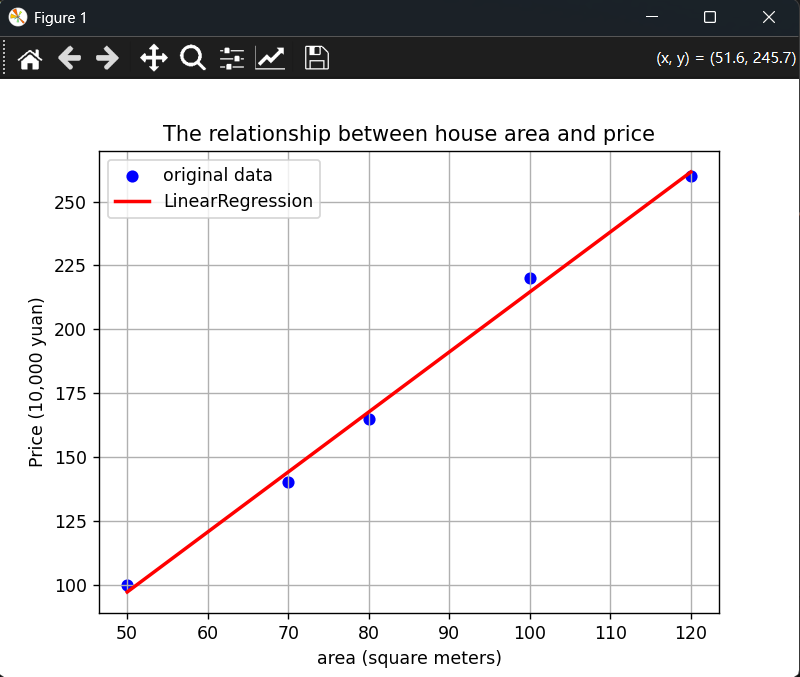
plt.scatter(X, y, color='blue', label='original data')# 2. 绘制拟合出的直线
# 使用模型的predict方法来生成直线上的点,这样最准确
y_pred = model.predict(X)
plt.plot(X, y_pred, color='red', linewidth=2, label='LinearRegression')# 3. 添加图表元素
plt.title('The relationship between house area and price')
plt.xlabel('area (square meters)')
plt.ylabel('Price (10,000 yuan)')
plt.legend() # 显示图例
plt.grid(True) # 显示网格
plt.show()