模块化神经网络

本文参考文章： Modular Deep Learning

什么是Modular Deep Learning

模块化神经网络（Modular Neural Network）是一种将复杂的深度学习系统分解为一系列功能相对独立、可重复使用的子网络（称为“模块”或“专家”）的架构设计；其核心思想是通过一个动态的“路由”机制，针对不同的输入或任务，灵活地选择并组合一个或多个最相关的专用模块进行计算，而非让整个庞大的网络处理所有信息，从而在实现​​功能专业化​​（每个模块专注于学习一项特定技能或知识）、​​参数高效性​​（无需为每个新任务训练整个模型，只需训练或调用小型模块）和​​系统组合性​​（将不同模块像乐高积木一样组装以解决新问题）之间取得平衡，最终目标是提升模型的泛化能力、可扩展性以及可解释性。

一个简单的例子：多语言翻译系统

为了让这个概念更加具体易懂，我们以一个​​多语言机器翻译系统​​为例，来拆解模块化是如何工作的。

背景与挑战

假设我们有一个强大的核心翻译模型（基座模型），我们希望它既能翻译英文到中文（En->Zh），也能翻译法文到德文（Fr->De）。传统的做法是分别对同一个基座模型进行两次完整的微调，得到两个独立的模型副本。这会导致：

• ​​参数低效​​：存储两个几乎一样大的模型，浪费存储空间。
• 知识隔离​​：两个模型学到的翻译知识无法共享，例如它们都可能从“学习正确的语法结构”中受益，但却各自为政。
• ​​负迁移​​：如果在单一模型上混合训练所有语言对，性能可能会因不同语言数据的干扰而下降。

模块化解决方案

我们采用模块化设计，具体采用​​适配器（Adapter）和​​ 固定路由（Fixed Routing）的策略。

• 基座模型（Shared Core）​​：一个在大规模多语言文本上预训练好的模型，拥有强大的通用语言理解和生成能力。​​其参数保持冻结（Frozen）​​，不被更新。

• ​​模块（Modules）​​：我们为每种目标语言引入一个小的适配器模块。例如：

  • Adapter_ZH：专门学习如何生成地道的中文。
  • Adapter_DE：专门学习如何生成地道的德文。

• ​​路由（Routing）​​：路由策略非常简单直接（​​固定路由​​）。系统根据用户指定的​​目标语言​​来选择对应的适配器。

  • 当用户请求翻译成​​中文​​时，路由机制激活 Adapter_ZH。
  • 当用户请求翻译成​​德文​​时，路由机制激活 Adapter_DE。

• 工作流程​​：

用户输入一句英文或法文句子。基座模型处理输入句子，生成一个中间的、与语言无关的语义表示。​​路由机制​​根据用户选择的“翻译为中文”或“翻译为德文”指令，​​自动选择​​并调用相应的目标语言适配器（Adapter_ZH或 Adapter_DE）。被选中的适配器接收基座模型的中间表示，并负责将其转换为符合目标语言习惯的最终输出。最终生成流畅的中文或德文译文。

模块化带来的优势

• 参数高效​​：我们只需要存储一个庞大的基座模型和几个轻量的适配器。新增语言（如日文）只需训练一个新的 Adapter_JA，成本极低。
• 避免干扰​​：训练Adapter_ZH（用英中数据）和Adapter_DE（用法德数据）互不干扰，因为它们是完全独立的参数集。
• 组合性与零样本泛化​​：这是最强大的优势。假设我们只有英中平行语料和法德平行语料，​​没有​​英德平行语料。传统方法无法直接做英德翻译。但模块化系统可能通过组合​​基座模型（的通用能力） + Adapter_DE​​ 来实现合理的​​零样本（Zero-shot）​​ 英德翻译，因为基座模型学到了某种程度的语言间对齐，而Adapter_DE知道如何生成德文。这就实现了1+1>2的组合效应。

符号系统：统一模块化研究的数学语言​​

基础模型的形式化​​

首先，作者将一个普通的神经网络 fθ​:X→Y定义为一组子函数（如神经网络层）的组合（∘）：

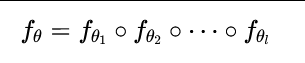
其中，θi​是第 i个子函数的参数。

模块化改造的核心：三大组合方式​​

作者明确指出，对于任何一个子函数 fθi​​，可以通过以下三种基本方式引入模块化参数 ϕ：

• ​​参数组合（parameter composition）：​​
  
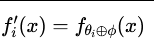
  • 操作​​：⊕代表参数层面的操作，如元素加法。
  • ​​实例​​：LoRA (Low-Rank Adaptation) 是典型代表。它通过低秩分解 θi​+BA来修改原始权重，实现高效适配。
  • 优势​​：极其参数高效，推理时无需改变模型结构。
• ​​输入组合（parameter composition）：​
  
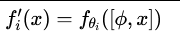
  • ​​操作​​：[⋅,⋅]代表拼接。将模块参数 ϕ作为额外输入与原始输入 x拼接。
  • ​​实例​​：Prompt Tuning、Prefix Tuning。通过拼接可学习的提示（prompt）向量来引导模型行为。
  • 优势​​：概念简单，但可能因增加序列长度而影响训练和推理效率。
• ​​函数组合：
  
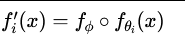
  • ​​操作​​：∘ 代表函数组合。将一个全新的函数（模块）插入到原有计算图中。
  • ​实例​​：Adapter Layers。在Transformer层中插入一个带有降维-非线性-升维结构的瓶颈层。
  • ​​优势​​：功能强大，性能优异，但会增加计算图和参数量。

路由与聚合的形式化​​

有了模块后，就需要管理它们。为此，作者引入了路由和聚合函数的数学表述：

• ​​路由函数 r(⋅)​​：其核心是产生一个​​路由分数向量 α​​。这个函数可以：
  • 是​​固定的​​（基于专家知识，如任务ID、语言ID）。
  • ​可学习的​​ rρ​(⋅)，参数为 ρ（通过输入 x或表征 h动态计算）。
  • 输出 α可以是​​硬路由​​（二进制向量，α∈{0,1}∣M∣）、​​软路由​​（概率分布，α∈[0,1]∣M∣）或​​未归一化的分数​​。
• 聚合函数 g(⋅)​​：接收路由分数 α和所有模块的输出集合 H，将其融合为最终输出 y。方式多样，可以是加权平均、注意力机制或简单的拼接。

这是对模块化计算的终极抽象：

从四个独立视角阐述该问题

本文通过四大维度分类现有方法：
1.​​计算函数（Computation）​​：模块如何实现（参数组合、输入组合、函数组合）。
2.​​路由函数（Routing）​​：如何选择激活模块（固定路由、学习路由）。
3.​​聚合函数（Aggregation）​​：如何合并模块输出（参数平均、表示平均等）。
4.​​训练设置（Training）​​：如何训练模块（多任务学习、持续学习、参数高效微调）。

计算函数（Computation）

Parameter Composition

路由函数（Routing）

聚合函数（Aggregation）

训练设置（Training）