9.9元奶茶项目:matlab+FPGA的cordic算法(双曲线向量模式)计算对数log
闲言碎语
知识无价,但学习有价,计划推出食品级FPGA项目系列。
* 4.9冰淇淋项目:只要少吃一个冰淇淋,就可以解锁一个 冰淇淋项目(matlab+fpga)。
* 9.9奶茶项目:只要少点一杯奶茶,就可以解锁一个奶茶项目(matlab+fpga)。
* 19.9咖啡项目:只要少点一杯咖啡,就可以解锁一个咖啡项目(matlab+fpga)。
* 29.9汉堡项目:只要少点一个汉堡,就可以解锁一个汉堡项目(matlab+fpga)。
……
目录
一、cordic算法计算自然对数log的原理
二、Matlab+FPGA仿真验证结果
三、代码
1、百度网盘链接
2、Matlab代码
3、FPGA代码
4、FPGA仿真代码
一、cordic算法计算自然对数log的原理
在 MATLAB 和 FPGA 上使用 CORDIC 算法计算自然对数 (ln) 是一项高效且资源友好的技术。CORDIC 通过简单的移位和加法操作来逼近数学函数,非常适合在硬件中实现。我会为你解释其核心原理、步骤,并提供 MATLAB 和 FPGA (Verilog) 的实现代码。
CORDIC 算法在双曲向量模式 (Hyperbolic Vectoring Mode) 下可以计算自然对数。其核心思想是通过一系列预定义的微旋转(迭代),将初始向量旋转至某个目标状态,从而提取出角度信息,该信息即为对数值。
计算自然对数的关键步骤和公式如下:
1. 预处理与范围调整: CORDIC 双曲模式计算 ln(x) 时,其收敛范围有限。为了处理更一般的正输入 x,需要先将其规格化:
* 将输入 x 分解为:x = m * 2^k (其中 k 为整数,m 为规格化后的尾数,通常调整到区间 [0.5, 2)或 [1, 4)等算法收敛范围内)。* 因此,ln(x) = ln(m) + k * ln(2)。* 这样,问题就转化为计算 ln(m)(m在收敛区间内)再加上一个已知常数 k*ln(2) 的缩放
。
2. 双曲向量模式迭代: 对调整后的值 m(处于收敛区间),应用 CORDIC 算法计算 ln(m)。其迭代公式(双曲向量模式)为:
* x_{i+1} = x_i + d_i * (y_i >> i)(>> i表示算术右移 i 位,即乘以 2^{-i})* y_{i+1} = y_i + d_i * (x_i >> i)* z_{i+1} = z_i - d_i * atanh(2^{-i})* 其中,旋转方向 d_i = -sign(y_i)(向量模式下,目标是使 y 趋于 0)。* 在双曲系统中,某些迭代步(如 i=4,13,40,121,... 等,即满足 i=3k+1 的索引)需要重复以确保收敛
。
3. 初始值与结果提取:
* 初始化:通常取 x0 = m + 1, y0 = m - 1, z0 = 0。* 经过 n 次迭代后,y_n将趋近于 0。此时,ln(m) ≈ 2 * z_n
。
* 最终,ln(x) = 2 * z_n + k * ln(2)。
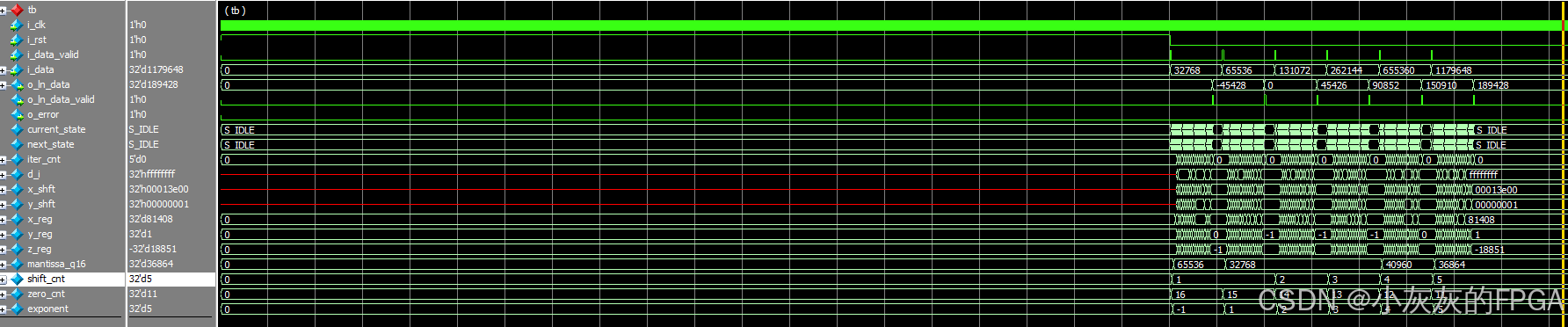
二、Matlab+FPGA仿真验证结果
Matlab中仿真验证结果,通过cordic算法和Matlab自带函数进行比对

FPGA的仿真结果如下:

三、代码

详情见下文:
9.9元奶茶项目:matlab+FPGA的cordic算法(双曲线向量模式)计算对数log
