9.9元奶茶项目：matlab+FPGA的cordic算法(向量模式)计算相位角

闲言碎语
知识无价，但学习有价，计划推出食品级FPGA项目系列。

• 4.9冰淇淋项目：只要少吃一个冰淇淋，就可以解锁一个 冰淇淋项目(matlab+fpga)。
• 9.9奶茶项目：只要少点一杯奶茶，就可以解锁一个奶茶项目(matlab+fpga)。
• 19.9咖啡项目：只要少点一杯咖啡，就可以解锁一个咖啡项目(matlab+fpga)。
• 29.9汉堡项目：只要少点一个汉堡，就可以解锁一个汉堡项目(matlab+fpga)。

……

目录

一、cordic算法求解相位角
二、Matlab+FPGA仿真验证结果
三、代码
1、百度网盘链接
2、Matlab代码
3、FPGA代码
4、FPGA仿真代码

一、cordic算法求解相位角

CORDIC（Coordinate Rotation Digital Computer）算法是一种非常巧妙且高效的计算方法，它主要用加法和移位这两种简单的运算来替代复杂的乘法等运算，从而计算三角函数、双曲函数等多种数学函数，其中包括计算相位角（即向量的角度或反正切值）。
CORDIC算法计算相位角（通常指计算 atan2(y, x)）的核心思想，是通过一系列预先确定的、角度不断减小的旋转（称为“微旋转”）来逼近目标向量（x, y）与X轴正方向的夹角。这些微旋转角度的正切值都是2的负幂次（即 tan(θ_i) = 2^(-i), i = 0, 1, 2, …），这使得复杂的乘法运算可以被高效的移位操作所替代。

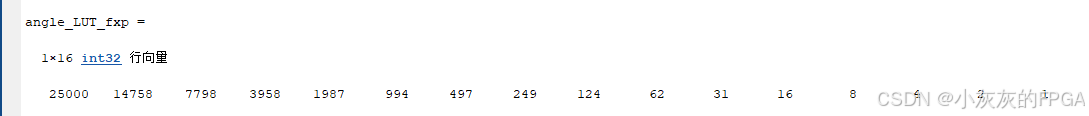
CORDIC算法在计算相位角时，通常采用向量模式（Vectoring Mode）。在向量模式下，CORDIC算法的目的是将一个给定的向量 (x, y) 旋转至X轴正方向（即让旋转后的y坐标趋近于0）。每次微旋转的方向 d_i（取+1或-1）由当前向量的y分量的符号决定：
* 若当前 y_i >= 0，则顺时针旋转（d_i = -1）
* 若当前 y_i < 0，则逆时针旋转（d_i = +1）

每次迭代不仅更新向量的坐标，还会在一个角度累加器（z） 中累加（或减去）本次旋转的角度值。其迭代公式为
* xi+1=xi−di⋅yi⋅2^(-i)
* yi+1=yi+di⋅xi⋅2^(-i)
* zi+1=zi−di⋅arctan(2^(-i))

经过多次（n次）的迭代后，y_n→0，此时角度累加器z_n中存储的值就是原始向量 (x, y) 的相位角估计值（θ≈z_n）
CORDIC算法因其硬件友好性，被广泛应用于：
* 数字下变频(DDC)：用于计算信号的幅度和相位。
* 软件定义无线电(SDR)：用于调制和解调。
* 电机控制：用于矢量变换和控制。
* 图像处理：用于旋转和变换操作。

二、Matlab+FPGA仿真验证结果

输入x=577,y=1000，Matlab仿真结果：

输入x=-577,y=1000，Matlab仿真结果：

输入x=-577,y=-1000，Matlab仿真结果：

输入x=577,y=-1000，Matlab仿真结果：

输入x=1732,y=1000，Matlab仿真结果：

输入x=-1732,y=1000，Matlab仿真结果：

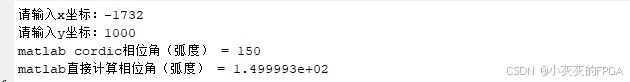
输入x=-1732,y=-1000，Matlab仿真结果：

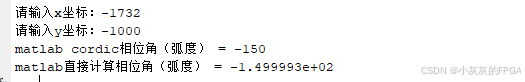
输入x=1732,y=-1000，Matlab仿真结果：

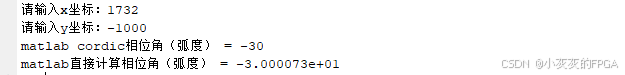
输入x=1000,y=1000，Matlab仿真结果：

输入x=-1000,y=1000，Matlab仿真结果：

输入x=-1000,y=-1000，Matlab仿真结果：

输入x=1000,y=-1000，Matlab仿真结果：

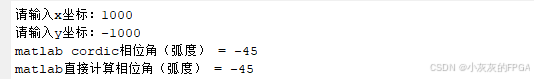
FPGA的仿真结果如下：

三、代码

详情见链接：
9.9元奶茶项目：matlab+FPGA的cordic算法(向量模式)计算相位角