当前位置：首页 > news >正文

解析01背包

news 2025/9/26 9:03:42

一、问题分析与动态规划思路

二、二维DP数组实现（基础版）

三、空间优化（一维DP数组）

四、示例验证

五、总结

01背包问题是动态规划中的经典问题，它的核心是在物品只能选或不选的约束下，求背包能容纳的最大价值（本题中为重量）。下面我们从思路分析、代码实现到空间优化，一步步深入讲解。

一、问题分析与动态规划思路

问题定义

有 n  个物品，每个物品有体积 v_i  和重量 w_i ，背包最大体积为 V 。每个物品只能选或不选，求背包能装的最大重量。

动态规划状态定义

我们定义 dp[i][j]  表示前 i  个物品，背包体积为 j  时的最大重量。

状态转移方程

对于第 i  个物品（注意数组下标从0开始，所以代码中是 i-1  索引），有两种选择：

- 不选： dp[i][j] = dp[i-1][j] （继承前 i-1  个物品的状态）。
- 选：如果当前物品体积 v_i ≤ j ，则 dp[i][j] = dp[i-1][j - v_i] + w_i （选了第 i  个物品，剩余体积 j - v_i  装前 i-1  个物品的最大重量，加上当前物品重量）。

综上，状态转移方程为：

dp[i][j] = \begin{cases}
dp[i-1][j] & \text{if } v_i > j \\
\max(dp[i-1][j],\ dp[i-1][j - v_i] + w_i) & \text{if } v_i \leq j
\end{cases}

二、二维DP数组实现（基础版）

先看基础的二维动态规划实现，代码如下：

#include <vector>
class Solution {
public:int knapsack(int V, int n, vector<vector<int>>& vw) {// dp[i][j]：前i个物品，背包体积j时的最大重量vector<vector<int>> dp(n + 1, vector<int>(V + 1, 0));for (int i = 1; i <= n; i++) {  // 遍历物品for (int j = 1; j <= V; j++) {  // 遍历背包体积if (vw[i-1][0] <= j) {  // 当前物品体积<=背包剩余体积，可选择“选”或“不选”dp[i][j] = max(dp[i-1][j], dp[i-1][j - vw[i-1][0]] + vw[i-1][1]);} else {  // 物品体积超过背包剩余体积，只能“不选”dp[i][j] = dp[i-1][j];}}}return dp[n][V];}
};

思路解释：

- 初始化 dp[0][j] （前0个物品，即没有物品）时，最大重量为0； dp[i][0] （背包体积为0）时，最大重量也为0。
- 外层循环遍历每个物品，内层循环遍历每个可能的背包体积，根据状态转移方程更新 dp 数组。

三、空间优化（一维DP数组）

观察状态转移方程可以发现， dp[i][j] 只依赖于 dp[i-1][...] （即上一层的状态）。因此可以将二维数组优化为一维数组，降低空间复杂度。

优化思路

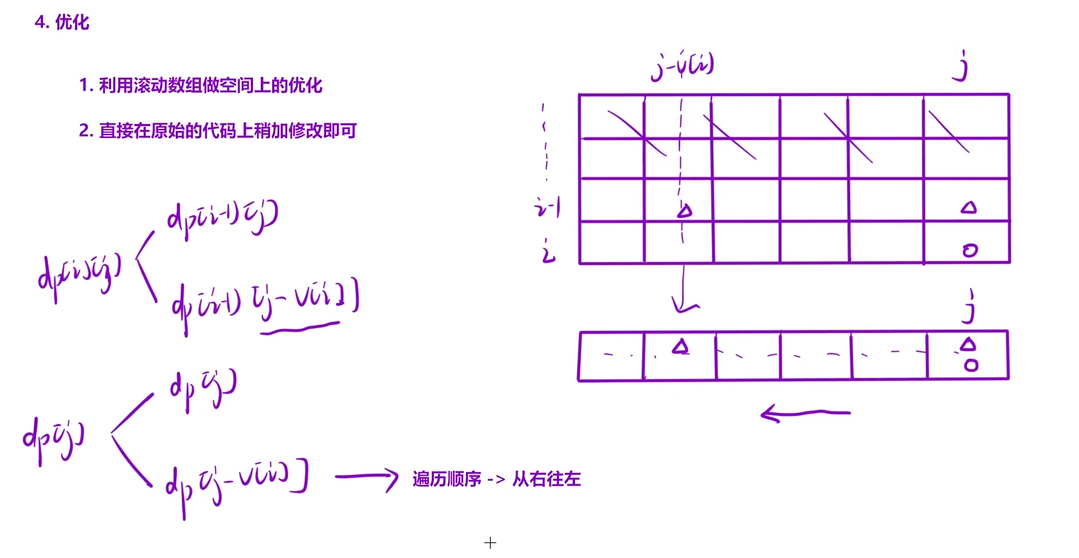
用 dp[j] 表示背包体积为 j 时的最大重量。此时需要逆序遍历背包体积，避免同一物品被重复选择（保证每个物品只选一次，符合01背包的约束）。

优化后的代码如下：


#include <vector>
class Solution {
public:int knapsack(int V, int n, vector<vector<int>>& vw) {// dp[j]：背包体积为j时的最大重量vector<int> dp(V + 1, 0);for (int i = 1; i <= n; i++) {  // 遍历物品// 逆序遍历背包体积，避免物品重复选择for (int j = V; j >= vw[i-1][0]; j--) {dp[j] = max(dp[j[j dp[j - vw[i-1][0]] + vw[i-1][1]);}}return dp[V];}
};

思路解释：

- 逆序遍历背包体积 j ，使得每次更新 dp[j] 时， dp[j - v_i] 还是“上一层”（即不包含第 i 个物品）的状态，保证了每个物品只被选一次。
- 空间复杂度从 O(n \times V) 优化到 O(V)，时间复杂度仍为 O(n \times V)，满足题目“进阶 O(n \cdot v)”的要求。

四、示例验证

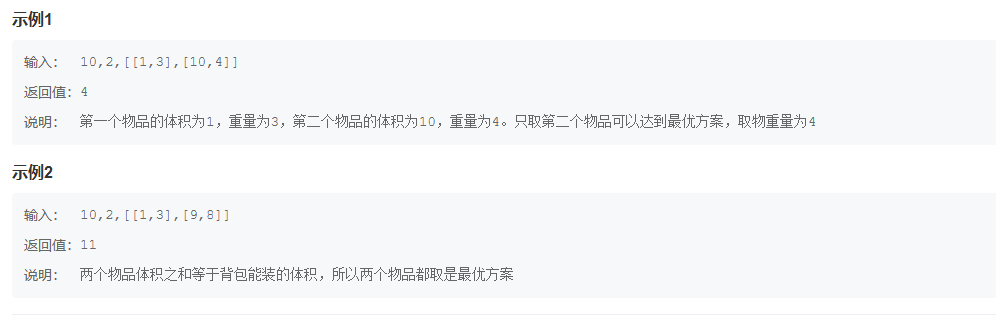
以题目中的示例1为例：

- 输入： V=10, n=2, vw=[[1,3],[10,4]]
- 二维DP过程：
- 当 i=1 （第一个物品，体积1，重量3）：
- 对于 j≥1 ， dp[1][j] = max(dp[0][j], dp[0][j-1]+3) = 3 （因为 dp[0][j]  是0）。
- 当 i=2 （第二个物品，体积10，重量4）：
- 当 j<10  时，只能不选， dp[2][j] = dp[1][j] = 3 ；
- 当 j=10  时， dp[2][10] = max(dp[1][10]=3, dp[1][0]+4=4) ，所以结果为4。
- 一维DP过程：
- 初始 dp = [0,0,0,...,0] （长度11）。
- 处理第一个物品（体积1，重量3）：
- 逆序遍历 j=10  到 j=1 ， dp[j] = max(dp[j[j dp[j-1]+3) ，最终 dp = [0,3,3,...,3] （共10个3）。
- 处理第二个物品（体积10，重量4）：
- 逆序遍历 j=10  到 j=10 ， dp[10] = max(3, dp[0]+4)=4 ，最终结果为4。

两种方法都能正确得到示例的返回值 4 。