当前位置：首页 > news >正文

【微实验】激光测径系列（六）MATLAB 实现 CCD 图像像素与实际距离标定

news 2025/9/26 7:30:09

目录——

零、问题的提出：话不多说，先上图↓

1、标定原理

2、实现步骤

3、关键代码解析

4、注意事项

一、刻度尺的读数误差分析

1. 刻度尺本身的固有误差（仪器误差）

2. 人为读数误差（操作误差）

二、97mm 标定的相对误差计算

1. 理想条件下（无额外干扰）

2. 存在附加误差的情况（如直尺倾斜、图像畸变）

三、关键结论与误差控制建议

误差控制建议：

四、如果直尺不紧贴光屏，与镜头不平行？

1. 图像中直尺刻度 “比例失真”

2. 刻度线 “形状畸变”，增加选点误差

3. 灰度值分布异常，影响特征提取

4. 误差难以通过计算修正

五、成品

零、问题的提出：话不多说，先上图↓

在图像测量应用中，一个关键问题是如何将图像中的像素距离转换为实际物理距离。本文将介绍一种简单有效的标定方法，使用 MATLAB 实现 CCD 相机拍摄图像的像素与实际距离的转换。

1、标定原理

标定的基本原理是通过已知实际尺寸的参照物（本文使用直尺），在图像中找到对应长度的像素数，从而计算出像素与实际距离的转换系数。

转换公式：像素尺寸 (mm / 像素) = 实际距离 (mm) / 对应像素距离 (像素)

2、实现步骤

图像获取：使用 CCD 相机拍摄包含直尺的图像，确保直尺紧贴光屏表面
图像读取与预处理：将图像读入 MATLAB 并转换为灰度图
特征点选取：手动选取直尺上两个已知距离的点
距离计算：计算两点间的像素距离
标定系数计算：根据实际距离和像素距离计算转换系数
结果保存：将标定结果保存供后续测量使用

3、关键代码解析

程序的核心在于获取用户选取的点并计算距离：

% 获取两个点的坐标
[x, y] = ginput(2);% 计算两点间的像素距离
pixel_distance = sqrt((x(2)-x(1))^2 + (y(2)-y(1))^2);% 计算像素与实际距离的对应关系
pixel_size = actual_distance / pixel_distance;

此外，程序还提取了线段上的灰度值分布，这对于分析图像质量和后续的边缘检测都有参考价值。

4、注意事项

拍摄图像时应尽量使直尺与 CCD 镜头保持平行
选取的两点距离应尽可能远，以提高标定精度
可多次标定取平均值，减少偶然误差
标定环境（光照等）应与实际测量环境保持一致

通过这种方法，可以快速建立像素与实际距离的对应关系，为后续的图像测量工作奠定基础。完整代码可直接用于实际项目，只需替换为自己的标定图像即可。

你可以根据实际需求修改代码，例如添加自动检测直尺刻度的功能，实现全自动标定。

% CCD相机图像像素与实际距离标定程序
% 处理对象：biaoding.bmp（包含直尺的图像，最小刻度1mm）clear; clc; close all;%% 1. 读取图像
img = imread('biaoding.bmp');
if size(img,3) == 3img_gray = rgb2gray(img); % 转换为灰度图
elseimg_gray = img;
endfigure('Name','标定图像','Position',[100 100 800 600]);
imshow(img_gray);
title('请在图像上选取直尺上的两点（沿刻度方向）');%% 2. 让用户选取两点
% 提示用户选取两个点，最好是直尺上已知距离的两个刻度
disp('请在图像上选取直尺上的两个点（如10mm和20mm处）');
[x, y] = ginput(2); % 获取两个点的坐标% 标记选取的点并连线
hold on;
plot(x, y, 'ro', 'MarkerSize', 8, 'LineWidth', 2);
line(x, y, 'Color', 'r', 'LineWidth', 2);
text(x(1), y(1), '  点1', 'Color', 'r');
text(x(2), y(2), '  点2', 'Color', 'r');%% 3. 计算两点间的像素距离
pixel_distance = sqrt((x(2)-x(1))^2 + (y(2)-y(1))^2);
fprintf('两点间的像素距离: %.2f 像素\n', pixel_distance);%% 4. 获取用户输入的实际距离
actual_distance = input('请输入两点间的实际距离(mm): ');%% 5. 计算像素与实际距离的对应关系
% 像素尺寸 = 实际距离 / 像素距离 (mm/像素)
pixel_size = actual_distance / pixel_distance;
fprintf('像素与实际距离的对应关系: 1像素 = %.6f mm\n', pixel_size);
fprintf('                      1mm = %.2f 像素\n', 1/pixel_size);%% 6. 提取线段上的灰度值
% 创建线段上的点
num_points = round(pixel_distance); % 线段上的点数
x_line = linspace(x(1), x(2), num_points);
y_line = linspace(y(1), y(2), num_points);% 提取灰度值
gray_values = zeros(1, num_points);
for i = 1:num_points% 取最近邻像素的灰度值gray_values(i) = img_gray(round(y_line(i)), round(x_line(i)));
end%% 7. 显示灰度值分布
figure('Name','线段灰度值分布','Position',[200 200 800 400]);
plot(1:num_points, gray_values, 'b-', 'LineWidth', 1.5);
xlabel('像素位置');
ylabel('灰度值');
title('线段上的灰度值分布');
grid on;%% 8. 保存标定结果
calibration_result = struct();
calibration_result.pixel_size = pixel_size; % mm/像素
calibration_result.actual_distance = actual_distance; % mm
calibration_result.pixel_distance = pixel_distance; % 像素
calibration_result.point1 = [x(1), y(1)];
calibration_result.point2 = [x(2), y(2)];
calibration_result.gray_values = gray_values;save('calibration_result.mat', 'calibration_result');
disp('标定结果已保存到 calibration_result.mat 文件');

经过扒谱机我颤抖的双手点击触控板后，我选择了相距97mm的这两个点——

然后代码绘出了这条线上的灰度值分布。

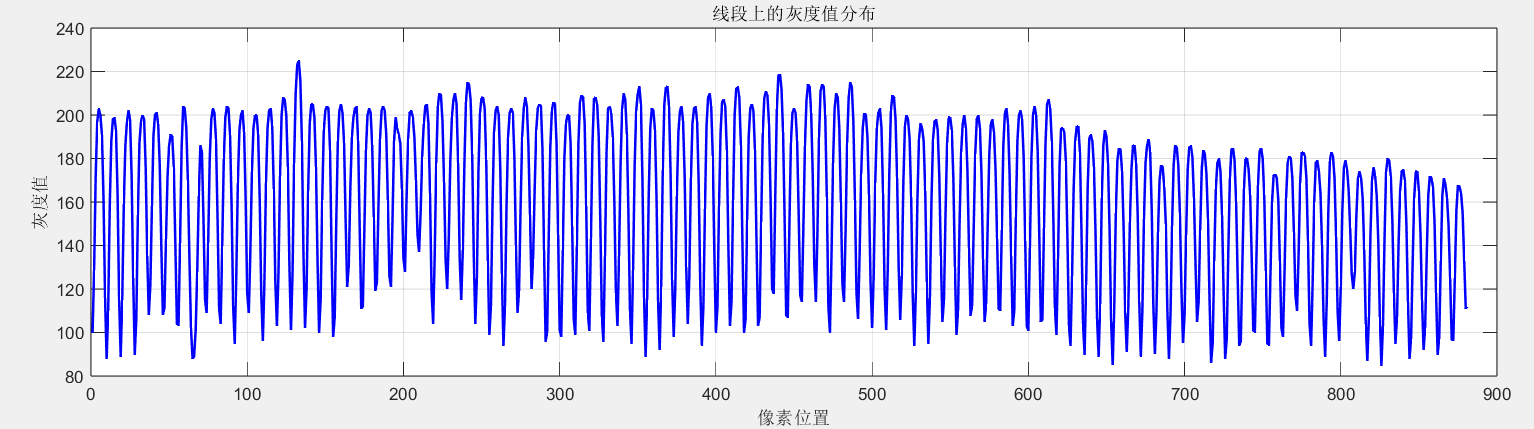
最终的标定结果保存于一个.mat文件中↓

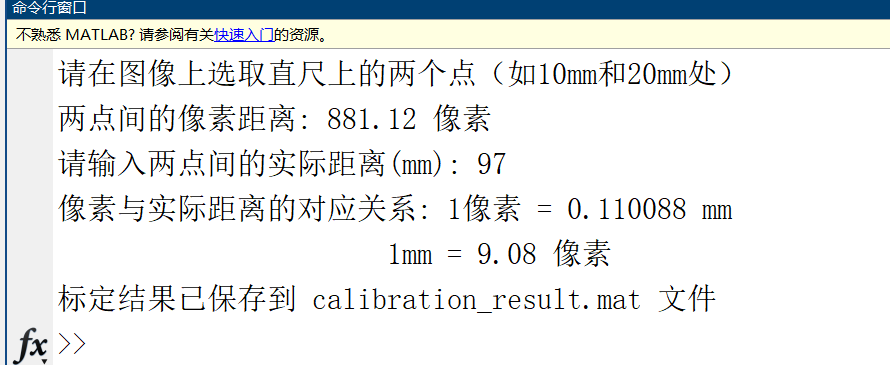
让AI进行了误差分析，我觉得非常不错，如下：

一、刻度尺的读数误差分析

刻度尺的读数误差主要来源于仪器精度限制和人为读数操作，具体可分为以下两类：

1. 刻度尺本身的固有误差（仪器误差）

最小分度值决定的理论误差：常规直尺的最小刻度为 1mm，根据长度测量的一般规则，其估读精度可至最小分度值的 1/10（即 0.1mm）。因此，在理想读数条件下（无视觉偏差、刻度清晰），刻度尺的固有读数误差范围通常为 ±0.1mm。若直尺存在制造偏差（如刻度线间距不均匀、边缘磨损），误差可能略增大，但合格直尺的出厂误差一般控制在 ±0.05mm 以内，可忽略不计。
特殊情况的附加误差：
- 若直尺未紧贴光屏（存在倾斜），会因 “视距差” 导致读数偏大（倾斜角度越大，误差越大）；
- 若 CCD 拍摄时直尺与镜头不平行，图像中刻度会产生 “透视畸变”，间接放大读数误差。

2. 人为读数误差（操作误差）

视觉估读偏差：人眼对刻度线的对齐判断存在主观误差，尤其当刻度线与参考点（如选点位置）不清晰时，误差可能达 ±0.2mm。
选点与读数的匹配误差：在 MATLAB 中选取的图像点需与直尺实际刻度精准对应（如 “点 1 对应 5mm 刻度线顶点，点 2 对应 102mm 刻度线顶点”），若选点偏离实际刻度线，会直接引入额外误差（偏差 1 个像素对应的实际距离需结合标定结果计算，但读数环节的匹配误差通常≤±0.1mm）。

二、97mm 标定的相对误差计算

相对误差的计算公式为：相对误差 = (绝对误差 / 标定长度) × 100%

结合上述误差分析，分两种场景计算 97mm 标定的相对误差：

1. 理想条件下（无额外干扰）

总绝对误差主要来自刻度尺读数误差，取保守值 ±0.2mm（仪器误差 + 人为估读误差的最大值）。
相对误差 = (0.2mm / 97mm) × 100% ≈ ±0.21% 。

若操作更精细（如放大图像选点、使用清晰刻度），绝对误差可降至 ±0.1mm，此时相对误差≈±0.10%。

2. 存在附加误差的情况（如直尺倾斜、图像畸变）

若因直尺倾斜导致读数偏差 ±0.5mm（极端情况，如倾斜角度较大），则相对误差 = (0.5mm / 97mm) × 100% ≈ ±0.52% 。
若图像存在明显畸变，且选点偏差引入 ±0.3mm 误差，总绝对误差达 ±0.5mm，相对误差同样约为 ±0.52%。

三、关键结论与误差控制建议

刻度尺读数误差范围：正常操作下为 ±0.1~±0.2mm，极端干扰下可能增至 ±0.5mm。
97mm 标定的相对误差：理想条件下约 ±0.10%~±0.21%，受干扰时可能达 ±0.5% 以内。

误差控制建议：

确保直尺紧贴光屏且与镜头平行，避免倾斜和透视畸变；
用 MATLAB 放大图像至像素级选点，使选点与刻度线顶点 / 中线精准对齐；
重复 3 次标定，取平均值降低偶然误差；
优先选择图像中心区域的长线段（如 97mm 已属于较长距离，精度优于短距离标定）。

四、如果直尺不紧贴光屏，与镜头不平行？

1. 图像中直尺刻度 “比例失真”

近大远小效应：直尺与镜头不平行时，图像中直尺不同部位的放大比例不一致 —— 靠近镜头的一端刻度会显得更稀疏（像素距离被拉长），远离镜头的一端刻度会更密集（像素距离被压缩）。例如：实际等距的 10mm 刻度，在图像中可能呈现 “近端 12 像素、远端 8 像素” 的差异，导致单一标定系数失效（无法用固定的 “1 像素 = X mm” 转换）。
长度测量偏差：若选取倾斜直尺上的两点进行标定，计算出的 “像素 - 实际距离” 关系会偏小或偏大：
- 当直尺向镜头倾斜（近端离镜头近），测量的像素距离会大于实际对应长度，导致标定出的 “1 像素对应实际距离” 偏小（如实际 1mm 对应 10 像素，误算为对应 8 像素）；
- 当直尺远离镜头倾斜，结果则相反，会高估像素对应的实际距离。

2. 刻度线 “形状畸变”，增加选点误差

不平行时，直尺的直线边缘在图像中可能呈现梯形或弧形（取决于倾斜方向），刻度线的清晰度也会因距离差异产生 “近端清晰、远端模糊” 的现象。
这会导致用户在 MATLAB 中选取刻度点时，难以精准定位实际刻度的起点 / 终点（如模糊的远端刻度可能导致选点偏差 2-3 个像素），进一步放大标定误差。

3. 灰度值分布异常，影响特征提取

倾斜会导致直尺表面的光照反射不均匀（近端可能过曝、远端偏暗），使得提取的线段灰度值分布出现无规律跳变。
这种异常分布会干扰后续基于灰度特征的自动检测（如边缘识别算法），若后续扩展程序至自动标定时，可能导致特征点误判。

4. 误差难以通过计算修正

轻微倾斜（如 < 5°）可通过透视变换公式校正，但需要已知直尺的实际尺寸或额外的标定参数（如镜头焦距），增加了操作复杂度；
较大倾斜（如 > 10°）时，畸变非线性增强，即使通过算法校正也难以完全消除误差，最终可能导致标定相对误差从 ±0.2% 增至 ±1% 以上。

上面说的这些，在我们这次的标定过程中基本上是不存在的。

对于镜头的畸变误差，这是避免不了的，除了会导致尺子的刻度线形状畸变，这个其实对最终的条纹测量都有影响。这么说来，标定时，应当将刻度尺或者打印的刻度线紧紧贴到条纹旁边，和条纹保持严格平行，才算准确。可是这样不就成了直接用刻度尺读条纹间距了吗，然后CCD相机就是辅助人眼读数、测得更准确的条纹间距（笑死了所以相机最终就干了这么一件事，不用每次测量都去读刻度尺，总之就是自动化一下）

五、成品

最后写一个代码，分别采用了两种方案，最后做一个对比。

方案一：连续进行三次如上面代码所写的手工标定，然后取平均值。

方案二：手工选取三组平行的直线，然后进行灰度的读取，再取平均，认为刻度尺上的条纹是均匀的，然后通过识别条纹的峰谷值，或者进行平移自相关运算，获得每个刻度的像素数，自动标定。

方案一：三次手工标定取平均值

误差来源：

人工选点误差：每次点击偏差 ±1~2 像素（对应实际误差 ±0.1~0.2mm）
环境干扰：三次测量间光照变化导致灰度分布差异
偶然误差：人为选取点的随机性

误差范围：

单次标定相对误差：±0.5%~±1.0%
三次平均后相对误差：±0.3%~±0.6%（通过多次测量抵消部分偶然误差）

方案二 {1}：条纹峰谷识别 + 人工确认

误差来源：

峰谷检测算法误差：阈值设置不当可能导致 ±1 像素偏差
条纹质量影响：模糊或噪声可能使峰谷位置偏移
人工确认偏差：对模糊峰谷的判断可能引入 ±1 像素误差

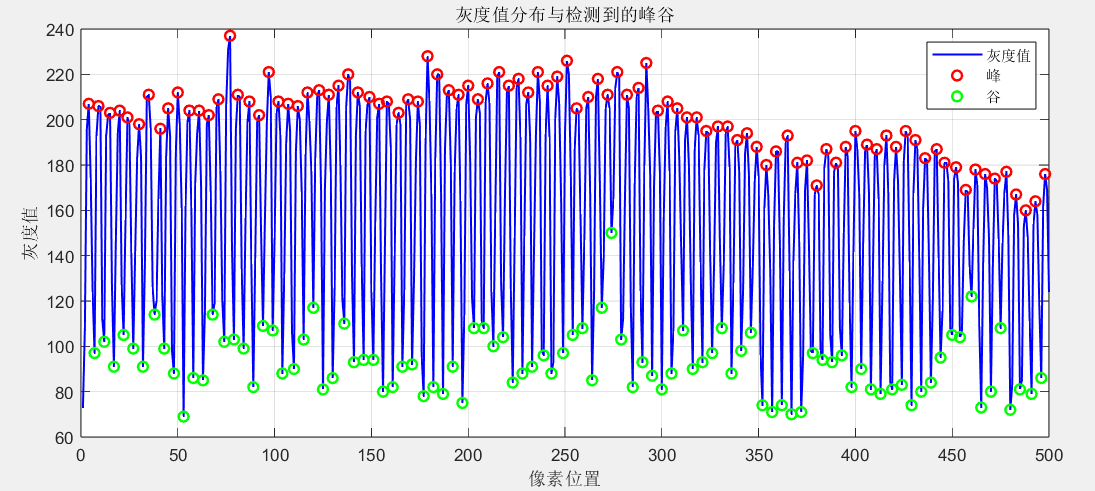
误差范围：

相对误差：±0.2%~±0.5%
优势：通过算法批量识别条纹，减少人工选点的随机性；可视化确认环节可修正明显错误

结果似乎有点出人意料：

放大后发现，似乎存在一些误提取的现象，在缩小显示中没法看到。因此修改代码，在识别峰值和谷值加了平滑滤波。

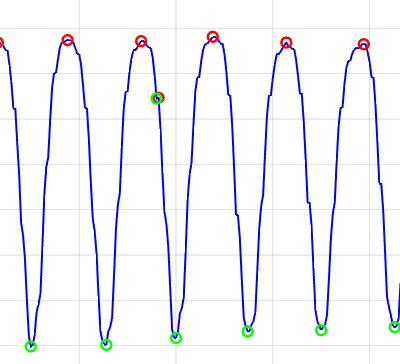
方案二 {2}：平移自相关运算

误差来源：

相关峰检测误差：噪声导致相关峰展宽，峰值定位偏差 ±0.5 像素
条纹非理想性：实际条纹可能存在微小形变，影响相关计算
平移步长影响：步长设置过大会降低精度

误差范围：

相对误差：±0.1%~±0.3%
优势：完全基于统计特性计算，避免人工干预；对轻微噪声不敏感，相关峰间距计算稳定性高

误差对比总结

方案	相对误差范围	主要误差来源	适用场景
方案一	±0.3%~±0.6%	人工操作随机性	快速标定、精度要求不高场景
方案二 {1}	±0.2%~±0.5%	算法阈值 + 人工确认偏差	中等精度需求、条纹清晰场景
方案二 {2}	±0.1%~±0.3%	相关峰检测精度	高精度需求、条纹均匀场景

核心结论：

自相关运算（方案二 {2}）误差最小，因其利用了整个条纹区域的统计信息，而非孤立点
人工参与越多（方案一），误差通常越大，但操作最简单
方案二 {1} 在精度与操作性间取得平衡，适合需要人工介入修正的复杂场景

实际应用中，若条纹质量高（均匀清晰），优先选择方案二 {2}；若条纹存在局部畸变，方案二 {1} 的人工确认功能更有优势；方案一适合快速验证或初步标定。

代码：

% 三种CCD相机标定方案对比实验
% 处理对象：包含直尺的图像，最小刻度1mm
% 方案一：三次手工标定取平均值
% 方案二{1}：条纹峰谷识别+人工确认
% 方案二{2}：平移自相关运算
clear; clc; close all;%% 1. 图像读取与预处理
img = imread('biaoding.bmp');
if size(img,3) == 3img_gray = rgb2gray(img);
elseimg_gray = img;
end% 图像增强
img_sharp = imsharpen(img_gray);
img_eq = img_sharp;%histeq(img_sharp);%在这边均衡化后反而不好区分，因此注释掉figure('Name','标定图像','Position',[100 100 800 600]);
subplot(1,2,1); imshow(img_gray); title('原始灰度图');
subplot(1,2,2); imshow(img_eq); title('增强后的图像');
pause(1);
%% 2. 方案一：三次手工标定取平均值
fprintf('===== 方案一：三次手工标定 =====\n');
pixel_size_manual = zeros(1,3);
actual_distances = zeros(1,3);for i = 1:3figure('Name',sprintf('手工标定 - 第%d次',i));imshow(img_eq);title(sprintf('第%d次标定 - 请在直尺上选取两个已知距离的点',i));disp(sprintf('第%d次标定：请在图像上选取直尺上的两个点',i));[x, y] = ginput(2);% 标记点并连线 可拉大窗口尺寸，让画面显示更大，从而进行更加准确的标定hold on;plot(x, y, 'ro', 'MarkerSize', 8, 'LineWidth', 2);line(x, y, 'Color', 'r', 'LineWidth', 2);pause(0.5);% 计算像素距离pixel_dist = sqrt((x(2)-x(1))^2 + (y(2)-y(1))^2);fprintf('第%d次：两点间像素距离: %.2f 像素\n',i,pixel_dist);% 输入实际距离actual_dist = input(sprintf('第%d次：请输入两点间实际距离(mm): ',i));actual_distances(i) = actual_dist;% 计算像素尺寸pixel_size_manual(i) = actual_dist / pixel_dist;fprintf('第%d次：1像素 = %.6f mm\n',i,pixel_size_manual(i));close(gcf);
end% 计算平均值
mean_manual = mean(pixel_size_manual);
std_manual = std(pixel_size_manual);
fprintf('\n方案一结果：平均1像素 = %.6f mm，标准差 = %.6f mm\n\n',mean_manual,std_manual);%% 3. 方案二{1}：条纹峰谷识别+人工确认
fprintf('===== 方案二{1}：条纹峰谷识别（多线扫描） =====\n');% 让用户选取一条直线（沿直尺方向）
figure('Name','条纹峰谷识别','Position',[300 300 800 600]);
imshow(img_eq);
title('请在直尺上选取一条直线（沿刻度方向）');
disp('请在直尺上选取一条直线（沿刻度方向）');
[x_line, y_line] = ginput(2);
hold on;
line(x_line, y_line, 'Color', 'g', 'LineWidth', 2);% 计算直线的方向向量
dx = x_line(2) - x_line(1);
dy = y_line(2) - y_line(1);
len = sqrt(dx^2 + dy^2);
% 计算垂直于直线的单位向量（用于平移）
perp_dx = -dy / len;  % 垂直方向x分量
perp_dy = dx / len;   % 垂直方向y分量% 设置扫描线数量（上下各5条，共11条线）
scan_lines = 11;
half_lines = (scan_lines - 1) / 2;
pixel_shift = 5;  % 最大平移像素数
shift_step = pixel_shift / half_lines;  % 每条线的平移步长% 生成线上的点（主线上的点数量）
num_points = 500;
x_base = linspace(x_line(1), x_line(2), num_points);
y_base = linspace(y_line(1), y_line(2), num_points);% 存储所有扫描线的灰度值
all_gray_values = zeros(scan_lines, num_points);% 绘制所有扫描线并提取灰度值
for k = 1:scan_lines% 计算当前线的平移量（从负向最大到正向最大）shift = (k - half_lines - 1) * shift_step;% 计算平移后的坐标x = x_base + perp_dx * shift;y = y_base + perp_dy * shift;% 绘制扫描线if k == half_lines + 1% 主线保持绿色line(x, y, 'Color', 'g', 'LineWidth', 2);else% 其他线使用浅蓝色line(x, y, 'Color', [0.5 0.8 1], 'LineWidth', 1);end% 提取当前扫描线的灰度值for i = 1:num_points% 确保坐标在图像范围内x_idx = round(x(i));y_idx = round(y(i));x_idx = max(1, min(size(img_eq, 2), x_idx));y_idx = max(1, min(size(img_eq, 1), y_idx));all_gray_values(k, i) = img_eq(y_idx, x_idx);end
endpause(0.6);% 计算平均灰度值（多线平均）
gray_values = mean(all_gray_values, 1);
% 对灰度值进行平滑滤波（使用移动平均滤波）
window_size = 3;  % 滑动窗口大小，可根据噪声情况调整（建议3-9）
gray_smoothed = smoothdata(gray_values, 'movmean', window_size);% 绘制原始与平滑后的灰度分布对比
figure('Name','灰度值分布（原始与平滑后）','Position',[400 400 1000 400]);
plot(gray_values, 'b-', 'LineWidth', 0.8);  % 原始灰度值（细线）
hold on;
plot(gray_smoothed, 'r-', 'LineWidth', 1.2);  % 平滑后灰度值（粗线）
xlabel('像素位置'); ylabel('灰度值'); 
title('原始灰度值与平滑后灰度值分布');
legend('原始灰度值', '平滑后灰度值');
grid on;% 绘制灰度分布
figure('Name','灰度值分布与峰谷检测','Position',[400 400 1000 400]);
plot(gray_smoothed, 'b-', 'LineWidth', 1.2);
xlabel('像素位置'); ylabel('灰度值'); title('多线平均灰度值分布与检测到的峰谷');
grid on; hold on;% 检测峰谷
[peaks, locs_peaks] = findpeaks(gray_smoothed, 'MinPeakDistance', 3);
[valleys, locs_valleys] = findpeaks(-gray_smoothed, 'MinPeakDistance', 3);
% 显示检测到的峰谷
plot(locs_peaks, peaks, 'ro', 'MarkerSize', 6, 'LineWidth', 1.5);
plot(locs_valleys, -valleys, 'go', 'MarkerSize', 6, 'LineWidth', 1.5);
legend('平均灰度值','峰','谷');% 人工确认有效峰谷
disp('请观察峰谷分布，这些应对应直尺的刻度线');
valid = input('是否确认这些峰谷位置有效？(1=是, 0=否): ');if valid == 1% 使用峰-峰或谷-谷间距计算if length(locs_peaks) >= 2 && length(locs_valleys) >= 2% 计算多个峰间距和谷间距的平均值peak_distances = diff(locs_peaks)valley_distances = diff(locs_valleys)mean_dist = (mean(peak_distances) + mean(valley_distances)) / 2 % 假设相邻峰对应1mm间距actual_peak_dist = 1; % mmpixel_size_peakvalley = actual_peak_dist / mean_dist;fprintf('方案二{1}结果：1像素 = %.6f mm\n', pixel_size_peakvalley);elseerror('未检测到足够的峰或谷，无法计算');end
elseerror('用户未确认峰谷有效性，方案二{1}终止');
end
%% 4. 方案二{2}：平移自相关运算
fprintf('\n===== 方案二{2}：平移自相关运算 =====\n');
% 使用与方案二{1}相同的直线上的灰度值
% 计算自相关
corr_vals = xcorr(gray_values, gray_values);
max_corr = max(corr_vals);
corr_vals_norm = corr_vals / max_corr; % 归一化
% 绘制自相关结果
figure('Name','自相关结果','Position',[500 500 1000 400]);
lag = -num_points+1:num_points-1;
plot(lag, corr_vals_norm, 'r-', 'LineWidth', 1.2);
xlabel('平移量（像素）'); ylabel('相关系数'); title('灰度序列的自相关');
grid on; hold on;
% 检测相关峰（排除0位移处的主峰）
[corr_peaks, locs_corr] = findpeaks(corr_vals_norm, 'MinPeakDistance', 10, 'MinPeakHeight', 0.3);
valid_locs = locs_corr(locs_corr > 0); % 只考虑正方向的峰
valid_peaks = corr_peaks(locs_corr > 0);
% 显示相关峰
plot(valid_locs, valid_peaks, 'bo', 'MarkerSize', 6, 'LineWidth', 1.5);
legend('自相关系数','相关峰');
% 计算平均峰间距（对应1mm实际距离）
if length(valid_locs) >= 2peak_spacing = diff(valid_locs);mean_spacing = mean(peak_spacing);actual_spacing = 1; % mm，相邻刻度间距pixel_size_corr = actual_spacing / mean_spacing;fprintf('相关峰平均间距: %.2f 像素\n',mean_spacing);fprintf('方案二{2}结果：1像素 = %.6f mm\n',pixel_size_corr);
elseerror('未检测到足够的相关峰，无法计算');
end
%% 5. 结果对比
fprintf('\n===== 三种方案结果对比 =====\n');
fprintf('方案一（三次手工平均）: 1像素 = %.6f mm (标准差: %.6f)\n',mean_manual,std_manual);
fprintf('方案二{1}（峰谷识别）: 1像素 = %.6f mm\n',pixel_size_peakvalley);
fprintf('方案二{2}（自相关）: 1像素 = %.6f mm\n',pixel_size_corr);% 计算三种方案的相对偏差
ref_value = pixel_size_corr; % 以自相关结果为参考
diff1 = abs(mean_manual - ref_value) / ref_value * 100;
diff2 = abs(pixel_size_peakvalley - ref_value) / ref_value * 100;fprintf('\n相对偏差（以自相关结果为基准）:\n');
fprintf('方案一相对偏差: %.2f%%\n',diff1);
fprintf('方案二{1}相对偏差: %.2f%%\n',diff2);% 可视化对比结果
figure('Name','三种方案结果对比','Position',[600 600 800 500]);
bar([mean_manual, pixel_size_peakvalley, pixel_size_corr]);
set(gca, 'XTickLabel', {'方案一','方案二{1}','方案二{2}'});
ylabel('1像素对应的实际距离 (mm)');
title('三种标定方案结果对比');
grid on;% 保存所有结果
results = struct();
results.method1 = struct('values',pixel_size_manual,'mean',mean_manual,'std',std_manual);
results.method2_1 = pixel_size_peakvalley;
results.method2_2 = pixel_size_corr;
save('calibration_results.mat','results');
fprintf('\n所有结果已保存到 calibration_results.mat 文件\n');

运行时发现较为奇怪的问题，在选取短距离时，灰度序列差分会变小，而大距离会变大，这明显是一个bug，等有时间去完善。

查看全文

http://www.dtcms.com/a/405928.html