【0基础学算法】前缀和(算法原理+经典例题)
文章目录
- 一维数组前缀和
- 题目链接
- 题目描述
- 解法
- 疑问:为什么下标要从1开始计算?
- 二维数组前缀和
- 题目链接
- 题目描述
- 解法
一维数组前缀和
题目链接
【模板】前缀和
题目描述

解法
解法一:暴力枚举
时间复杂度:O(n2)O(n^2)O(n2)
遍历数组求和即可,用下标0~r元素的和减去0~l元素的和,会超时。
解法二:前缀和
时间复杂度:O(1)O(1)O(1)
前缀和:快速求出数组中某一个连续区间的和
算法原理:
注意:使用前缀和算法的前提是数组的第一个元素下标必须从1开始
对于数组arr,{1,4,7,2,5,8, 3,6, 9}
- 预处理一个前缀和数组
dp,dp的下标也要从1开始
dp[i]表示arr的[1, i]区间的元素和
如何预处理dp呢?
采用递推的方式,因为有dp[1]=arr[1]dp[1] = arr[1]dp[1]=arr[1]的天然已知条件,所以我们可以从左往右依次把dp的所有元素递推出来。
递推公式:
dp[i]=dp[i−1]+arr[i]dp[i]=dp[i-1]+arr[i]dp[i]=dp[i−1]+arr[i]

2. 使用前缀和数组dp
看图:
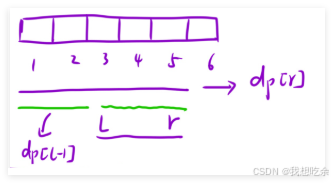
不难看出:
区间[l, r]的元素和为dp[r]−dp[l−1]dp[r] - dp[l-1]dp[r]−dp[l−1]
- 代码
#include <iostream>
#include<vector>
using namespace std;int main()
{//读入数据int n = 0, m = 0;cin >> n >> m;vector<int> arr(n + 1);for(int i = 1; i < n + 1; ++i) cin >> arr[i];//预处理一个前缀和数组vector<long long> dp(n + 1);//long long 防溢出for(int i = 1; i < n + 1; ++i) dp[i] = dp[i-1] + arr[i];//使用前缀和数组解决问题int l = 0, r = 0;while(m--){cin >> l >> r;cout << dp[r] - dp[l-1] << endl;}return 0;
}
疑问:为什么下标要从1开始计算?
其实是为了处理边界情况,初始化递推dp时,需要用上dp[i-1],如果下标从0开始计算,会导致越界访问,因此,我们需要一个在数组头部的辅助节点,这个节点的值必须为0,称作虚拟节点。
二维数组前缀和
题目链接
【模板】⼆维前缀和
题目描述

解法
解法一:暴力枚举
时间复杂度:O(n3)O(n^3)O(n3)
通过遍历二维数组求得目标区间的元素和,会超时
解法二:前缀和
时间复杂度:O(1)O(1)O(1)
与一维数组类似,二维数组下标也从1开始计算
以一个4行3列的二维数组arr为例:
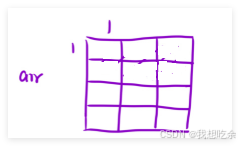
- 预处理一个前缀和矩阵(二维数组)
dp
dp与arr一样大dp[i][j]表示:在arr中,从(1,1)位置到(i,j)位置区间内的元素和
比如,(1,1)~(2,3)的区间和为该阴影区域:
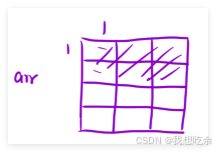
如何递推呢?
我们将dp划分为4个区域A、B、C、D,如图:
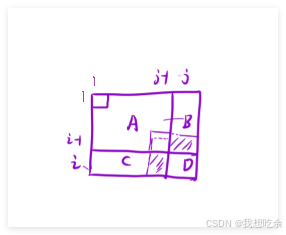
我们的目标是求dp[i][j]dp[i][j]dp[i][j]
dp[i][j]=A+B+C+Ddp[i][j] = A+B+C+Ddp[i][j]=A+B+C+D
直接求似乎并不好求,我们采用间接的方式:
B和C我们还需另外求,而(A+B)和(A+C)是已知的:
dp[i][j]=(A+B)+(A+C)+D−Adp[i][j] = (A+B)+(A+C)+D-A dp[i][j]=(A+B)+(A+C)+D−A
代入得:
dp[i][j]=dp[i−1][j]+dp[i][j−1]+arr[i][j]−dp[i−1][j−1]dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1]dp[i][j]=dp[i−1][j]+dp[i][j−1]+arr[i][j]−dp[i−1][j−1]
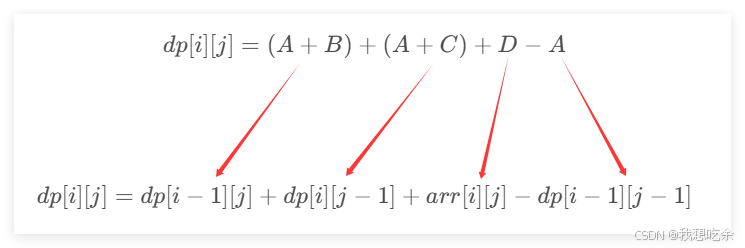
- 使用前缀和矩阵dp
求(x1,y1)~(x2,y2)
将dp划分为4个区域A、B、C、D,如图:
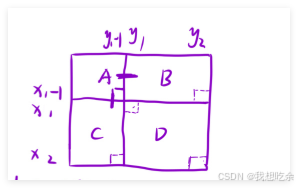
目标是求D区域。
同样是间接求法:
D=(A+B+C+D)−(A+B)−(A+C)+AD=(A+B+C+D) -(A+B)-(A+C)+AD=(A+B+C+D)−(A+B)−(A+C)+A
代入得:
D=dp[x2][y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]D = dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]D=dp[x2][y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]

- 代码
注意这里二维数组的定义方式,巧用匿名对象可以省不少功夫。
#include <iostream>
#include<vector>using namespace std;int main() {//输入int n = 0, m = 0, q = 0;cin >> n >> m >> q;vector<vector<int>> arr(n+1, vector<int>(m+1));for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j) cin >> arr[i][j];//预处理一个前缀和矩阵vector<vector<long long>> dp(n+1, vector<long long>(m+1));for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];//使用dp解决问题int x1 = 0, y1 = 0, x2 = 0, y2 = 0;while(q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;}return 0;
}
