当前位置：首页 > news >正文

机器学习之损失函数

news 2025/9/25 17:35:47

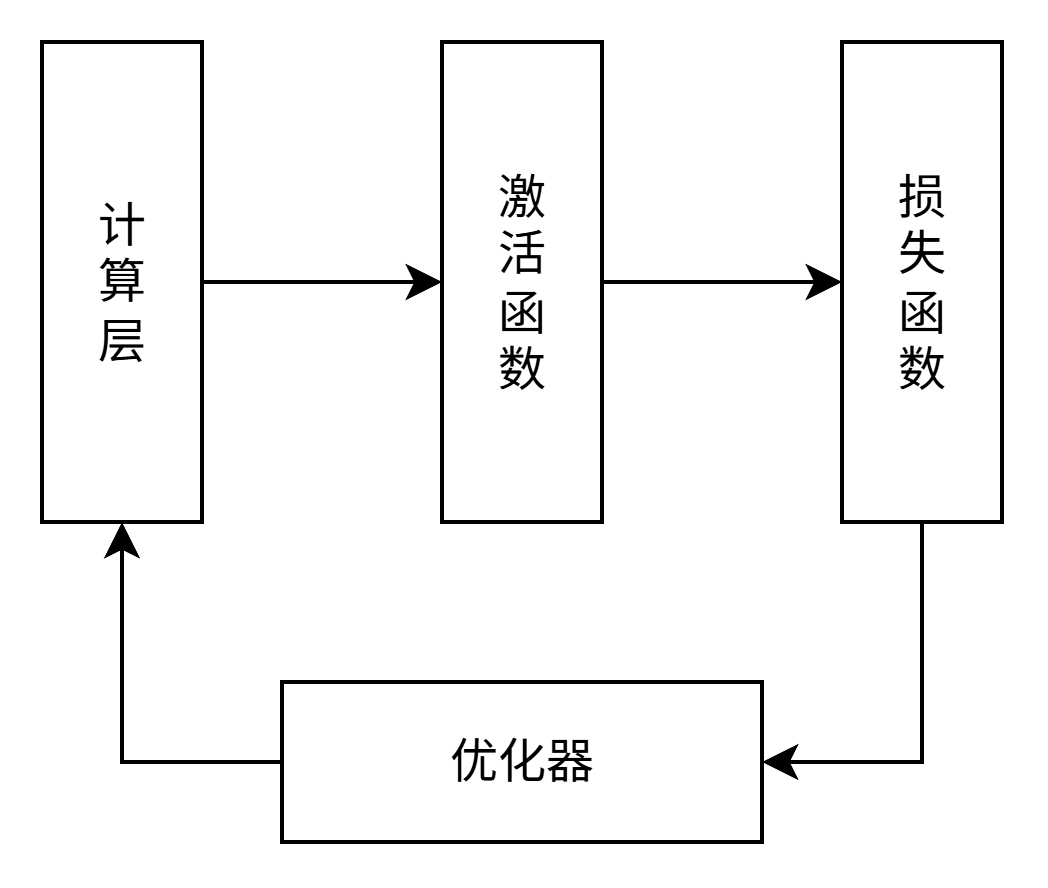
在训练过程中，神经网络模型可以简化为上图中的4部分，今天的主角是损失函数。损失函数的作用是量化模型预测值与真实值之间的差别，也就是负责告诉优化器模型错没错，错的有多离谱。优化器再根据损失函数的结果调整模型参数，模型训练的过程很像是一个负反馈网络。

严格来说，优化器利用的不是损失函数的结果，而是它的导数，也就是梯度。因此损失函数不一定具有零点，但是一定要有最低点(最小值)，也就是它的梯度一定要有零点。其次是它必须可导，这样才能求梯度。我们学到的第一个二次函数 $y=x^2$ 就是这样的函数。

为了方便描述，先对后面要用到的符号做一个说明：

符号	含义
$Y$	真实值(向量)
$Y_i$	真实值(向量)的第 $i$ 个值
$y$	模型预测值(向量)
$y_i$	模型预测值(向量)的第 $i$ 个值
$L$	损失函数

MAE及其变种

我们能想到的最简单的误差计算公式就是做减法， $Y_i-y_i|$ 这就是误差，它的函数图像如下。

损失函数定义为每项误差求和的平均：

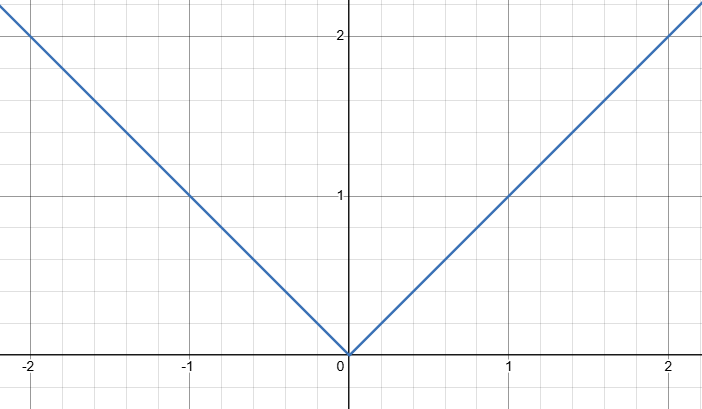
$L=1n∑i=0n∣Yi−yi∣L=\frac{1}{n}\sum_{i=0}^{n}{|Y_i-y_i|}$

这叫平均绝对误差(Mean Absolute Error)，俗称 MAE，也有叫它L1损失函数的。虽然它具有最小值，但是它在最小值处不可导。于是就衍生出了一些 MAE 的变体，它们都是分段函数，主要就是为了解决 MAE 零点不可导问题，比如Smooth L1损失函数。

$L={12(Y−y)2∣Yi−yi∣<1∣Y−y∣−12otherL=\begin{dcases} \frac{1}{2}(Y-y)^2 & |Y_i-y_i|<1 \\ |Y-y|-\frac{1}{2} & other \end{dcases}$

再比如Huber Loss：

$L={12(Y−y)2∣Yi−yi∣<δδ(∣Y−y∣−12δ)otherL=\begin{dcases} \frac{1}{2}(Y-y)^2 & |Y_i-y_i|<\delta \\ \delta(|Y-y|-\frac{1}{2}\delta) & other \end{dcases}$

它们的核心都是通过分段函数解决MAE零点附近不可导的问题，其他地方还是MAE。

MSE

MSE 叫做均方差，Mean Square Error。它是对误差的平方求和取平均，也被叫做L2损失函数。

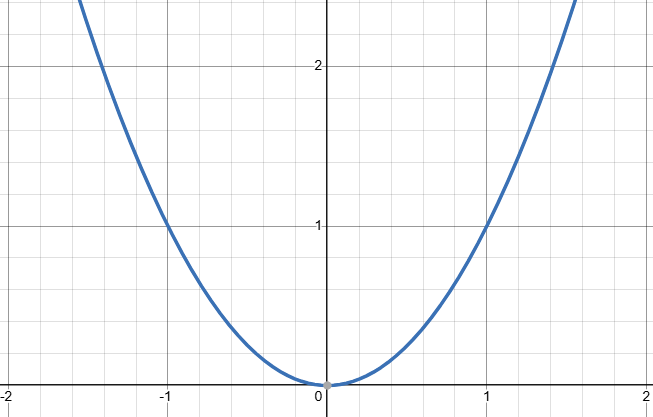
$L=1n∑i=0n(Yi−yi)2L=\frac{1}{n}\sum_{i=0}^{n}{(Y_i-y_i)^2}$

在线性回归中，常用它来拟合函数。它不经具有最小值，而且处处可导。

交叉熵

交叉熵是一种熵，一种什么样的熵呢？一种交叉的熵，什么是交叉的熵呢？首先要理解熵。物理学和信息论里都有熵的概率，这里是信息论中的熵。它的定义是：无损编码事件信息的最小平均编码长度。

关键词：最小，长度。

假设事件A出现的概率为 $p$ ，采用二级制编码，需要的长度为： $n=-\log_2{p}$ 。这也很好理解，所谓编码就是给样本空间中的每一个事件一个编号，事件A出现的概率为 $p$ ，要让事件A出现一次，需要的样本数量就是 $1p\frac{1}{p}$ ，而 $n$ 比特二进制所能表示的总可能性是 $2^n$ ，于是就有：

$2n=1plog⁡22n=log⁡21pn=−log⁡2p\begin{aligned} 2^n&=\frac{1}{p} \\ \log_2{2^n}&=\log_2\frac{1}{p} \\ n&=-\log_2{p} \end{aligned}$

熵其实就是所有事件编码长度的期望：

$E=−∑i=0npilog⁡2piE=-\sum_{i=0}^n{p_i\log_2{p_i}}$

记住这个结果是最小的，如果我们把模型输出结果也看作是一种概率分布，假设 $p_i$ 表示真实分布概率，而 $q_i$ 表示模型预测的概率分布，将上面公式中后面的 $p_i$ 换成 $q_i$ ，于是得到：

$Ec=−∑i=0npilog⁡2qiE_c = -\sum_{i=0}^n{p_i\log_2{q_i}}$

这就是交叉熵！所谓交叉就是把 $p_i$ 换成 $q_i$ ，前面我们说了熵是最小的长度，那么一定有 $Ec≥EE_c \geq E$ ，当且仅当 $q_i=p_i$ 时取等号。如果我们将 $E_c$ 做为损失函数，它也具有最小值，而且可导，这就是交叉熵损失函数。

KL散度

KL是两个人名，库尔贝克和莱布里埃。理解了交叉熵之后，其实KL散度就是交叉熵与熵的差！

$EKL=Ec−E=−∑i=0npilog⁡2qi+∑i=0npilog⁡2pi=∑i=0npilog⁡21qi+∑i=0npilog⁡2pi=∑i=0npilog⁡2piqi\begin{aligned} E_{KL}&=E_c-E\\ &= -\sum_{i=0}^n{p_i\log_2{q_i}}+\sum_{i=0}^n{p_i\log_2{p_i}} \\ &= \sum_{i=0}^n{p_i\log_2{\frac{1}{q_i}}}+\sum_{i=0}^n{p_i\log_2{p_i}} \\ &=\sum_{i=0}^n{p_i\log_2{\frac{p_i}{q_i}}} \end{aligned}$