当前位置：首页 > news >正文

速通ACM省铜第十四天赋源码（Coloring Game）

news 2025/9/25 17:28:01

引言：

Coloring Game

题意分析

逻辑梳理

代码实现

常规实现

优化

结语：

引言：

经过2天的挣扎，我还没开出来，那题的题目链接在这里Come a Little Closer（蒸不动了，你们有兴趣可以看一下这道题，真的神奇，E题我开出来了，D题我想俩天都不知道怎么打）。那么今天我们换一道题来打，今天我们来打一道CF评级1300的一道题

那么接下来，就进入今天的题目讲解啦————————>

Coloring Game

那么，按照惯例，我们先来看题目

题意分析

题目链接在这里Problem - 2112C - Codeforces

不想跳转的可看下图

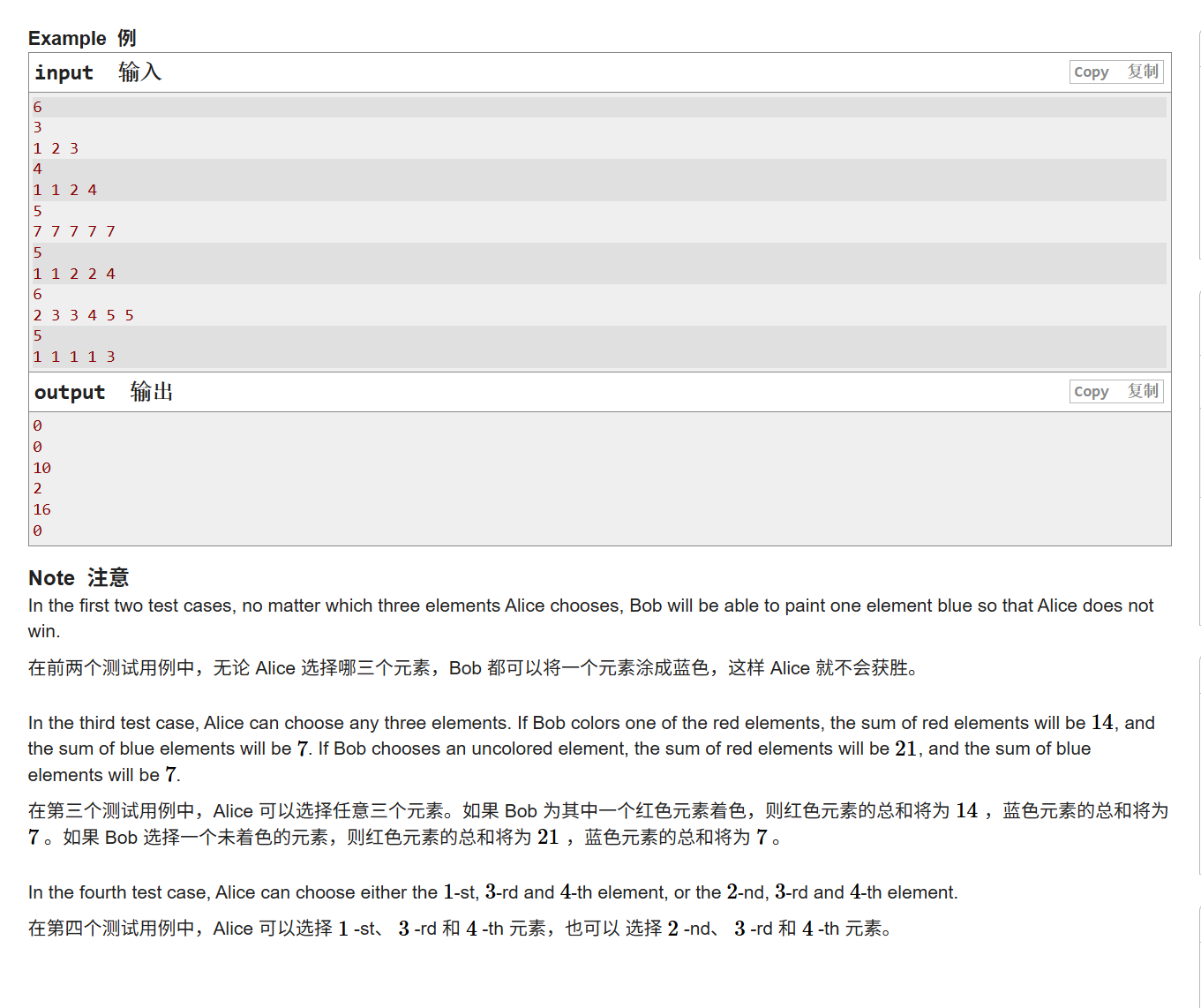
题目意思很简单，就是先给你一个有n个元素的数组，然后有俩个人，其中一个人先任选3个下标变成红色，之后另一个人任选一个下标变成蓝色，该题希望让第一个人获得胜利，胜利的条件时红色的数值加起来比蓝色高

然后让你输出有多少种选择方法可以让第一个人胜利

那么，题目分析完了，我们来梳理一下逻辑

逻辑梳理

首先，第二个人想要获胜，最好的染球的方式有俩种

一种是直接染数字最大的那个元素

还有一种是将第一个人染的三个元素里最大的那个元素的值给染成蓝色

那么想要让第一个人胜利，其实只需要满足俩个条件

1、3个元素中俩个小的元素加起来比3个元素中最大的元素大

2、3个元素加起来比整个数组中最大的元素大

只需要满足这俩个条件，这种选择就是肯定能胜利哒

最后只需要统计完符合条件的次数，然后输出次数即可

那么逻辑就梳理完啦，这道题逻辑很简单，代码实现也很简单，主要难在代码的优化，不优化的话就会TLE，那么接下来，就进入代码的实现环节

代码实现

那么，我们先来看看该题的常规实现的代码，这个代码很简单，那便是用三层循环即可，具体代码如下

常规实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
int a[5010];void solve()
{long long ans = 0;int n;cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];sort(a + 1, a + n + 1);for (int i = 1; i < n - 1; i++){for (int j = i + 1; j <= n - 1; j++){for (int k = j + 1; k <= n; k++){if (a[i] + a[j] > a[k] && a[i] + a[j] + a[k] > a[n])ans++;}}}cout << ans << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}

优化

但不出意外，三层循环，就算数组元素范围只有5000也经不起这么造，果然，TLE4了，如图

那么，我们就要尝试对这个代码进行优化

首先，我们先回归原来的式子，如图

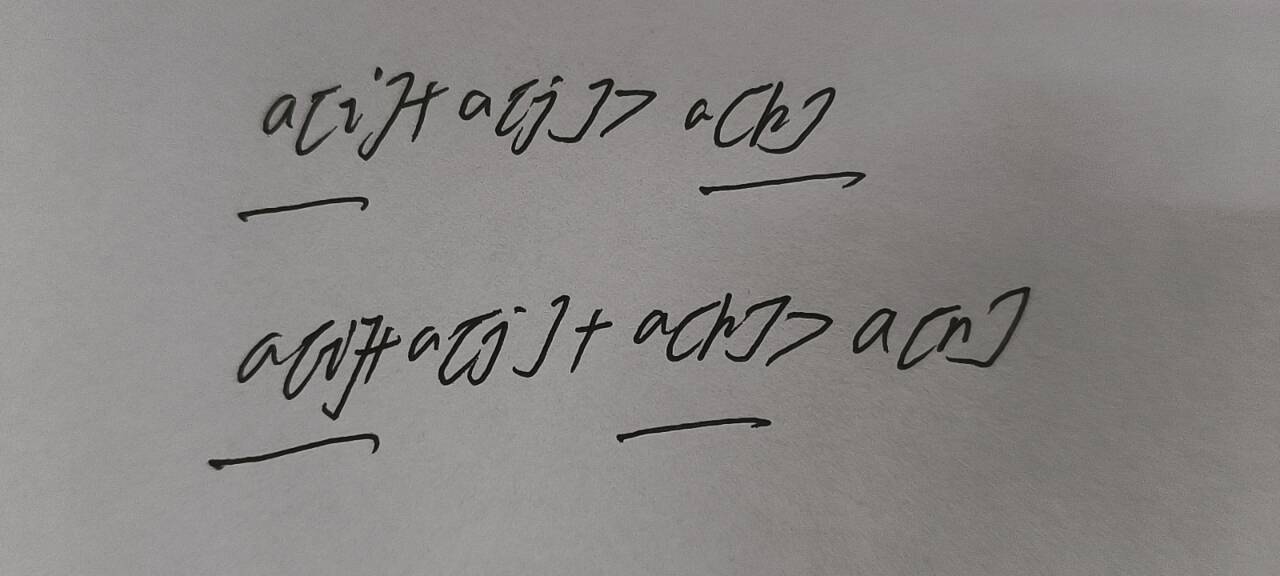
我们可以发现，直接ｉ，ｊ，ｋ这样遍历下去肯定是行不通的

那么，我们可以尝试通过固定俩个下标，然后来寻找第三个下标的下限或者上限，那很清楚，既然都是＞的关系，肯定是要找到下限

那么，我们肯定不能选择将ｉ跟ｊ定死，因为如果讲ｉ跟ｊ定死，ａ［ｋ］与ａ［ｎ］－ａ［ｋ］的这俩个值的关系并不好判断，上下限也不好找

那么这个时候我们可以固定最小的下标以及最大的下标，然后来找中间的下标

那么怎么找中间的下标，很简单，用二分就可以了

如果这俩个条件都满足，就返回一种情况

然后其他情况就返回另一种情况就可以了

只是需要特别注意的是，可能会存在都不符合或者边界也符合的情况，这种时候我们只需要加个特判就可以啦

然后找到最小的满足条件的下标后，返回ｋ－该下标即可，然后再将返回的值加到总值里就好啦

那么，代码的优化就讲解完啦，接下来，请看ＡＣ码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
int a[5010];int erfen(int left, int right, int i, int k, int n)
{if (left >= right){if (left == k)return 0;return k - right;}int mid = left + (right - left) / 2;if (mid == i)return k - right;if (a[i] + a[mid] > a[k] && a[i] + a[mid] + a[k] > a[n])return erfen(left, mid, i, k, n);elsereturn erfen(mid + 1, right, i, k, n);
}void solve()
{long long ans = 0;int n;cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];sort(a + 1, a + n + 1);for (int i = 1; i < n - 1; i++){for (int k = i + 2; k <= n; k++){if (a[k] * 3 <= a[n])continue;ans += erfen(i, k, i, k, n);}}cout << ans << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}

那么，这题就讲解完毕啦