3- 十大排序算法（基数排序、归并排序、快速排序、堆排序）

3- 十大排序算法（基数排序、归并排序、快速排序、堆排序）

七、基数排序(Radix sort)

• 基数排序：在位数比较小的情况下，即所有的数字差不多大时，是很好的方法。

• 以排序{5,47.23,19,17.31}为例。

• 第1步:先按个位的大小排序，得到(31，23,05,47，17,19}。

• 第2步:再按十位的大小排序，得到(05，17，19，23，31，47}。

def radix_sort(arr):# 如果数组为空，直接返回空列表if not arr:return arr# 找到数组中的最大值max_val = max(arr)# 从最低位开始，依次按位进行排序exp = 1  # exp 是当前排序位的权值，从1开始（个位）while max_val // exp > 0:# 根据当前位进行计数排序arr = counting_sort_by_digit(arr, exp)exp *= 10  # 移动到更高位return arrdef counting_sort_by_digit(arr, exp):# 创建一个计数数组，用来记录各个数字的出现次数n = len(arr)output = [0] * n  # 输出数组，存放排序后的结果count = [0] * 10  # 计数数组，用来统计每个数字（0-9）的出现次数# 统计每个数字的出现次数，放入计数数组for i in range(n):index = arr[i] // exp % 10  # 获取当前位上的数字count[index] += 1# 对计数数组进行累加，得到每个数字的最终位置for i in range(1, 10):count[i] += count[i - 1]# 根据计数数组将元素放到正确的位置i = n - 1while i >= 0:index = arr[i] // exp % 10  # 获取当前位上的数字output[count[index] - 1] = arr[i]count[index] -= 1i -= 1# 将排序后的数组复制回原数组for i in range(n):arr[i] = output[i]return arr# 输入一个数字列表
arr = list(map(int, input("请输入数字，用空格分隔：").split()))
sorted_arr = radix_sort(arr)  # 调用基数排序函数
print("排序后的列表：", sorted_arr)  # 输出排序后的列表

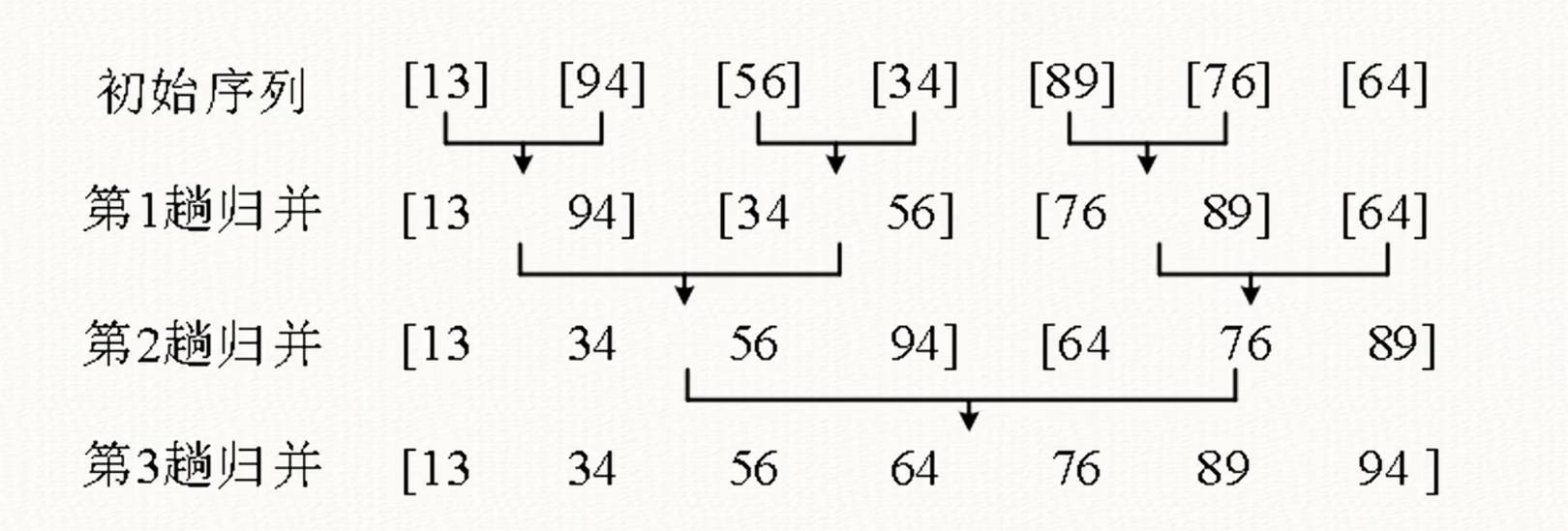
八、归并排序(Merge sort)

• 归并排序(Merge sort)：分治的妙用共logn趟归并每趟归并有0(n)次比较计算量0(nlogn)
• (1)分解。把初始序列分成长度相同的左右两个子序列，然后把每个子序列再分成更小的两个子序列.， 直到子序列只包含1个数。
• (2)求解子问题，对子序列排序。
• (3)合井。归井两个有序的子序列。

def merge_sort(arr):# 如果数组长度小于等于1，直接返回该数组（递归的终止条件）if len(arr) <= 1:return arr# 分治：将数组从中间分成两个子数组mid = len(arr) // 2left_half = arr[:mid]  # 左半部分right_half = arr[mid:]  # 右半部分# 递归调用merge_sort，对左右子数组分别排序left_half = merge_sort(left_half)right_half = merge_sort(right_half)# 合并两个已排序的子数组return merge(left_half, right_half)def merge(left, right):# 用于合并两个已排序的数组sorted_arr = []i = j = 0# 比较两个子数组的元素，按顺序放入新数组while i < len(left) and j < len(right):if left[i] < right[j]:sorted_arr.append(left[i])i += 1else:sorted_arr.append(right[j])j += 1# 如果左子数组中还有元素，直接将剩余部分添加到新数组while i < len(left):sorted_arr.append(left[i])i += 1# 如果右子数组中还有元素，直接将剩余部分添加到新数组while j < len(right):sorted_arr.append(right[j])j += 1return sorted_arr# 输入一个数字列表
arr = list(map(int, input("请输入数字，用空格分隔：").split()))
sorted_arr = merge_sort(arr)  # 调用归并排序函数
print("排序后的列表：", sorted_arr)  # 输出排序后的列表

九、快速排序(Merge sort)

• 快速排序:影响最大的排序算法，“The Top 10 Algorithms”，20世纪十大算法之一。分治的妙用计算量0(nlogn)。

• 思路：思路:把序列分成左右两部分，使得左边所有的数都比右边的数小;递归这个过程，直到不能再分为止。

• 如何把序列分成左右两部分?最简单的办法是设定两个空间X、Y和一个基准数t检查序列中所有的元素，比t小的放在X中，比t大的放在Y中。

  def quick_sort(arr):# 如果数组长度小于等于1，直接返回该数组（递归的终止条件）if len(arr) <= 1:return arr# 选择基准元素，这里选择数组的最后一个元素作为基准pivot = arr[-1]# 将数组分为两部分，左部分小于基准，右部分大于基准left = [x for x in arr[:-1] if x < pivot]  # 小于基准的元素right = [x for x in arr[:-1] if x >= pivot]  # 大于等于基准的元素# 递归地对左部分和右部分排序，并将排序结果与基准合并return quick_sort(left) + [pivot] + quick_sort(right)# 输入一个数字列表
  arr = list(map(int, input("请输入数字，用空格分隔：").split()))
  sorted_arr = quick_sort(arr)  # 调用快速排序函数
  print("排序后的列表：", sorted_arr)  # 输出排序后的列表
  

十、堆排序(Heap sort)

• 堆排序：用二又堆来排序，计算量0(nlogn)。

• 二叉堆:一棵二叉树，如果是一棵最小堆，那么树根是最小值。

• 性质:把树根取出后，新的树根仍然是剩下的树上的最小值。

• 把要排序的n个数放进二叉堆，然后依次取出树根，就从小到大排好了序。

• 堆是一种特殊的完全二叉树，具有以下性质

  • 1.完全二叉树结构:堆必须是一棵完全二叉树，即除了最后一层外，每一层都被完全填满，并且最后一层的节点从左到右填充。
  • 2.堆属性:
    • 大顶堆:每个节点的值都大于或等于其左右子节点的值。这意味着堆的根节点是所有节点中的最大值。
    • 小顶堆:每个节点的值都小于或等于其左右子节点的值。这意味着的根节点是所有节点中的最小值。

def heapify(arr, n, i):largest = i  # 假设当前节点为最大值left = 2 * i + 1  # 左子节点索引right = 2 * i + 2  # 右子节点索引# 如果左子节点比当前节点大，则将 largest 更新为左子节点if left < n and arr[left] > arr[largest]:largest = left# 如果右子节点比当前节点大，则将 largest 更新为右子节点if right < n and arr[right] > arr[largest]:largest = right# 如果 largest 发生变化，说明当前节点需要交换if largest != i:arr[i], arr[largest] = arr[largest], arr[i]  # 交换元素# 递归地对交换后的子树进行堆化heapify(arr, n, largest)def heap_sort(arr):n = len(arr)# 建立最大堆，从最后一个非叶子节点开始堆化for i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# 一个一个地提取元素（交换堆顶和堆尾），并对剩下的堆进行堆化for i in range(n - 1, 0, -1):arr[0], arr[i] = arr[i], arr[0]  # 交换堆顶和当前最后元素heapify(arr, i, 0)  # 对堆顶进行堆化# 输入一个数字列表
arr = list(map(int, input("请输入数字，用空格分隔：").split()))
heap_sort(arr)  # 调用堆排序函数
print("排序后的列表：", arr)  # 输出排序后的列表