学习2025.9.24

空洞卷积（Dilated Convolutions）

本质

在小卷积核的基础上提高感受野

计算

假设空洞卷积卷积核大小为，空洞数为，其等效卷积核大小为，则：

例如，一个3*3的卷积核，每一条边的空洞数为2，即每两个卷积像素之间有一个空洞，其等效卷积核大小为：

对于当前层的感受野，在已知上一层的感受野的情况下，可以得到：

表示当前层（i+1）之前所有层步长的乘积，即：

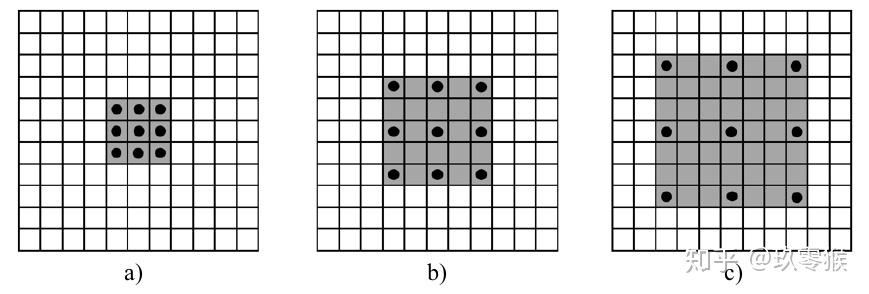
例如，在上面的图中，输入图像的感受野为1，第一层卷积（a）的感受野为3，第二层卷积（b）的计算如下：

第三层卷积（c）的感受野计算如下：

具体感受野的变化情况可以参考：

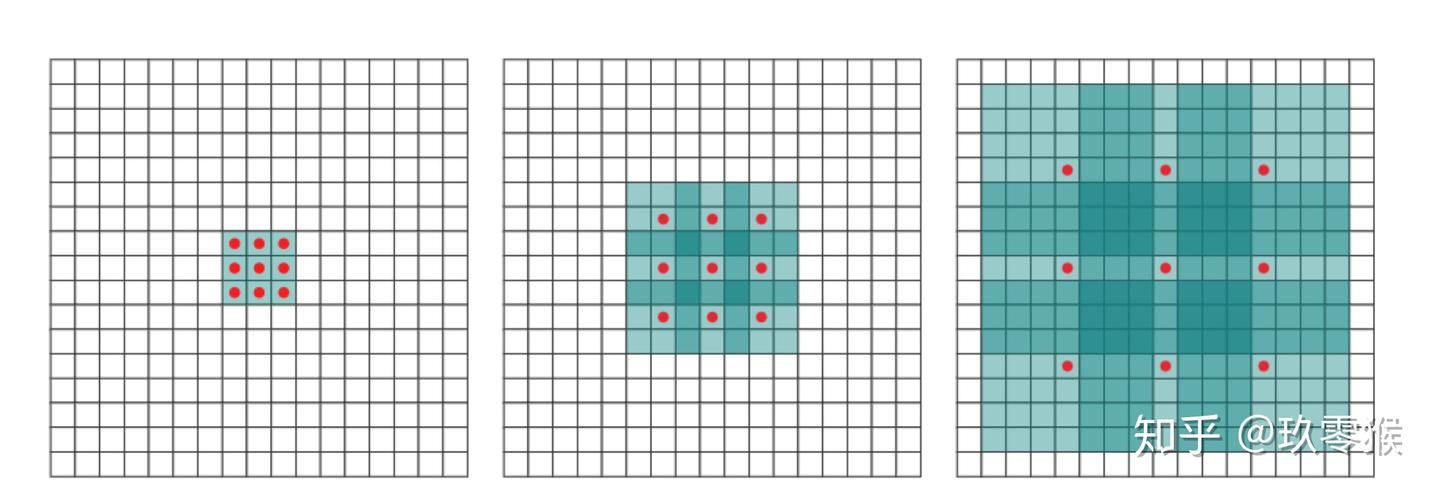
缺陷

（1）多次叠加同一dilation rate的卷积核会造成局部信息丢失：

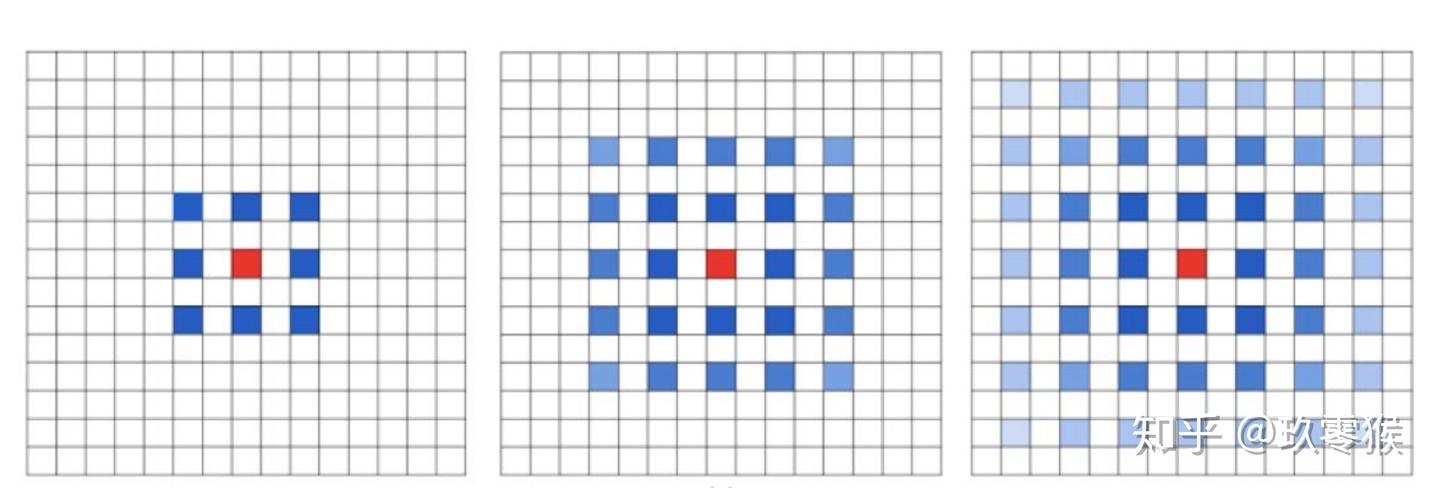
（2）远距离信息失去相关性

CSPLayer

本质

把输入通道一分为二，一部分直通保留原始信息，一部分进入残差/bottleneck模块做深度处理，最后再concat在一起，通过卷积融合；在特征图层面上融合了深层残差特征和直通浅层特征。

结构

Yolov5和Yolov8中CSPLayer的结构分别为：

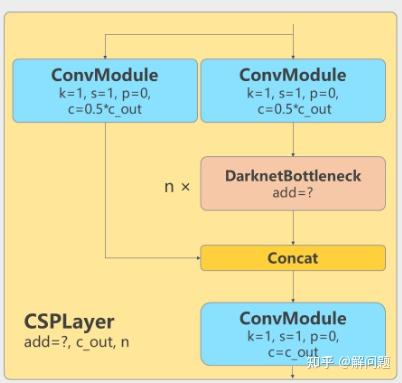
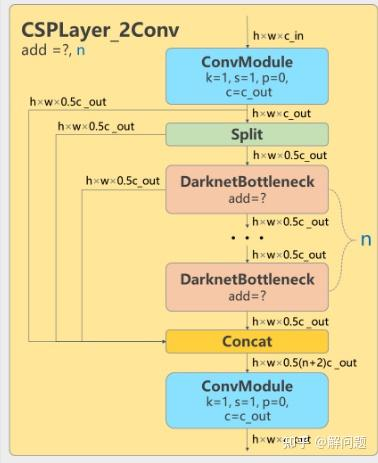
其中DarknetBottleneck的结构为：

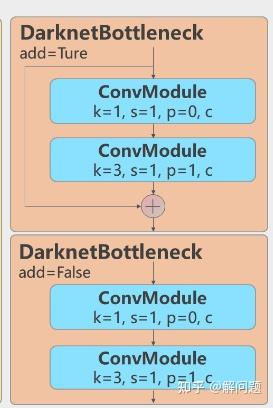
CBAM

本质

一种轻量级注意力模块，结合了通道注意力和空间注意力

结构

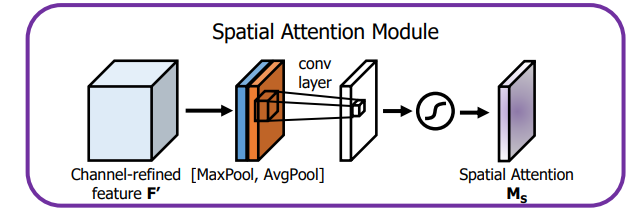
整体结构：

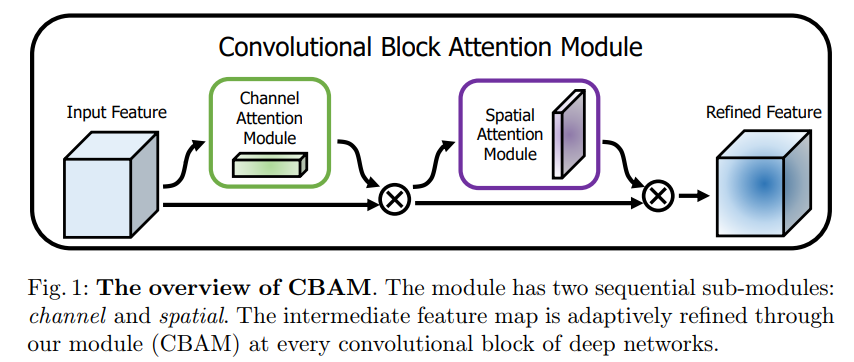
CAM（通道注意力）：通道维度不变，压缩空间维度，关注通道信息

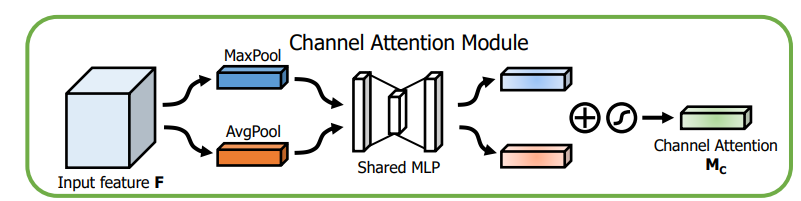
SAM（空间注意力）：空间维度不变，压缩通道维度，关注空间信息

上采样方法——Interpolation（插值）

最近邻法 (Nearest Interpolation)

将目标图像中的每个像素映射到原始图像中距离最近的像素，并将该像素的值复制到目标像素。

单线性插值

针对二维数据的插值方法，依据一次函数的特性进行计算：

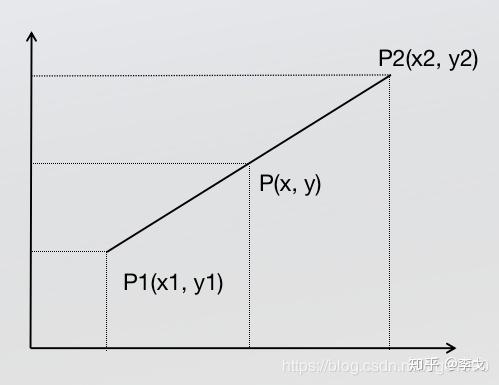
二维图像的插值可以看作是三维结构：图像长、宽以及每个像素的数值，这样，单线性插值即表代对x或y坐标以及像素数值两个维度进行计算。

双线性插值 (Bilinear Interpolation)

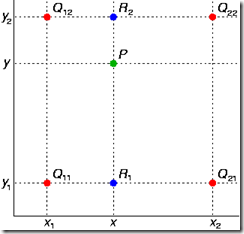
实际上，要对三维数据插值的话，可以先在x轴方向上计算R1和R2的单线性插值，再在y方向上计算P的插值。

双三次插值 (Bicubic interpolation)

双三次插值利用待采样点周围16个点的灰度值做三次插值，不仅考虑到4个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。

上采样方法——UnSampling

直接填充最临近的数值

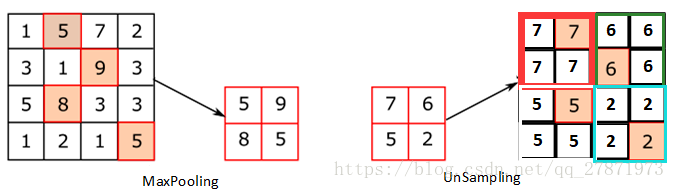
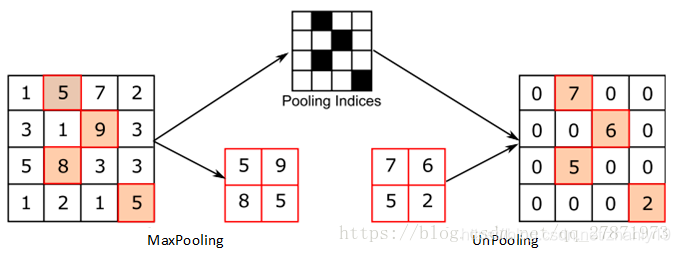
上采样方法——UnPooling

记录了最大池化中最大值的位置信息，其余位置补0

上采样方法——转置卷积

一个卷积矩阵可以看作是卷积核权重的重排，而一个卷积操作可以视为该卷积矩阵与展平的初始向量的乘积。这样，我们便可以通过一个可训练的卷积矩阵来实现“反卷积”的过程。