pytorch 线性回归

线性回归模型

线性模型

多个样本的公式为：

损失函数

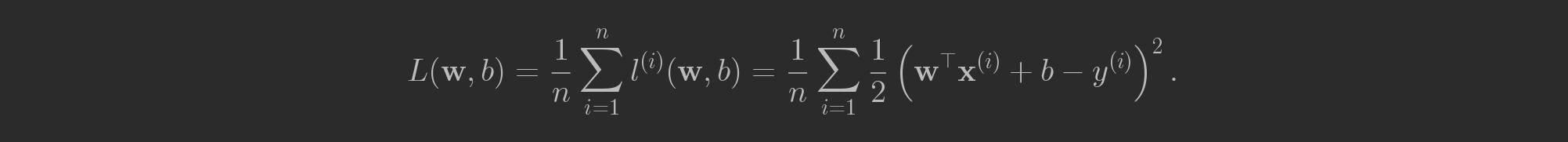
使用矩阵写为：

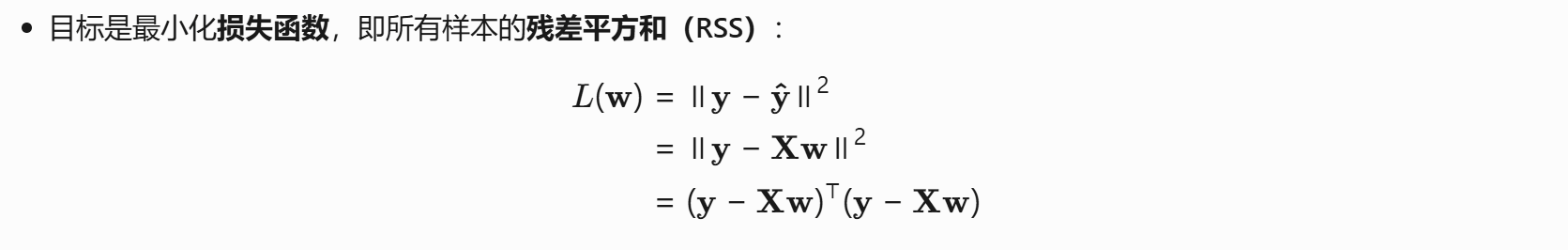
这里我们用范数来表示，然后将式子展开

这里的求导用到了微积分中给出的式子
最终可以得到解析解：

随机梯度下降

不是所有模型都能很方便的找到解析解，因此，在深度学习框架中一般使用的是随机梯度下降法。

用模型预测

略

矢量化加速

原理为向量计算，即SIMD。

n = 10000
a = torch.ones([n])
b = torch.ones([n])
d = a + b

张量可以直接相加，做向量计算。

正态分布与平方损失

之前我们用平方损失定义了线性回归的损失函数。
现在我们假设观测中的噪声也符合正态分布：

这时y也符合了某种正态分布。
接下来我们求y的最大似然估计：

我们发现最大似然估计的优化依赖的正是之前定义的平方损失函数。
由此得出结论：
在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。

注：线性回归的代码实现会放在李哥AI对应的章节。